2024版高考数学微专题专练39空间几何体的结构及其三视图和直观图理（附解析）

这是一份2024版高考数学微专题专练39空间几何体的结构及其三视图和直观图理（附解析），共8页。

[基础强化]
一、选择题
1．以下命题：
①以直角梯形的一腰所在直线为轴旋转一周所得的旋转体是圆台；②圆柱、圆锥、圆台的底面都是圆面；③用一个平面截圆锥，得到一个圆锥和一个圆台．
其中正确命题的个数为( )
A．0 B．1 C．2 D．3
2．用任意一个平面截一个几何体，各个截面都是圆面，则这个几何体一定是( )
A．圆柱
B．圆锥
C．球体
D．圆柱、圆锥、球体的组合体
3．已知正△ABC的边长为a，那么△ABC的平面直观图△A′B′C′的面积为( )
A．eq \f(\r(3),4)a2B．eq \f(\r(3),8)a2C．eq \f(\r(6),8)a2D．eq \f(\r(6),16)a2
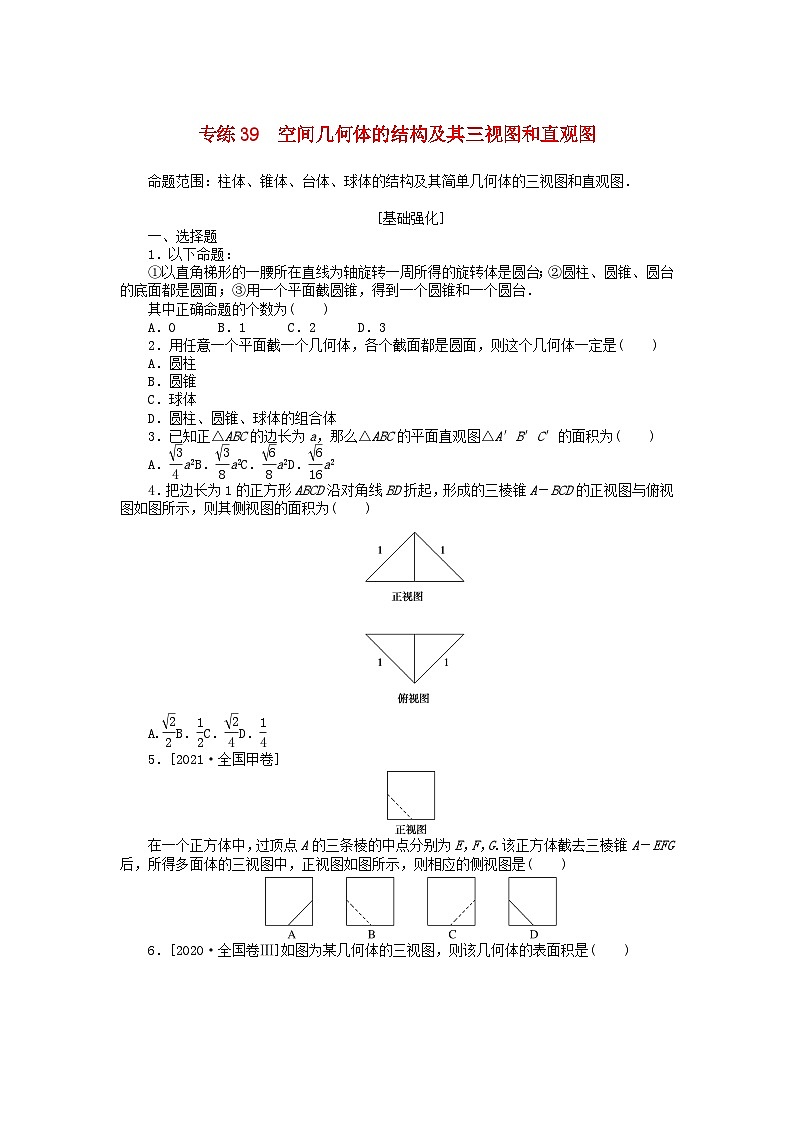
4．把边长为1的正方形ABCD沿对角线BD折起，形成的三棱锥A－BCD的正视图与俯视图如图所示，则其侧视图的面积为( )
A.eq \f(\r(2),2)B．eq \f(1,2)C．eq \f(\r(2),4)D．eq \f(1,4)
5．[2021·全国甲卷]
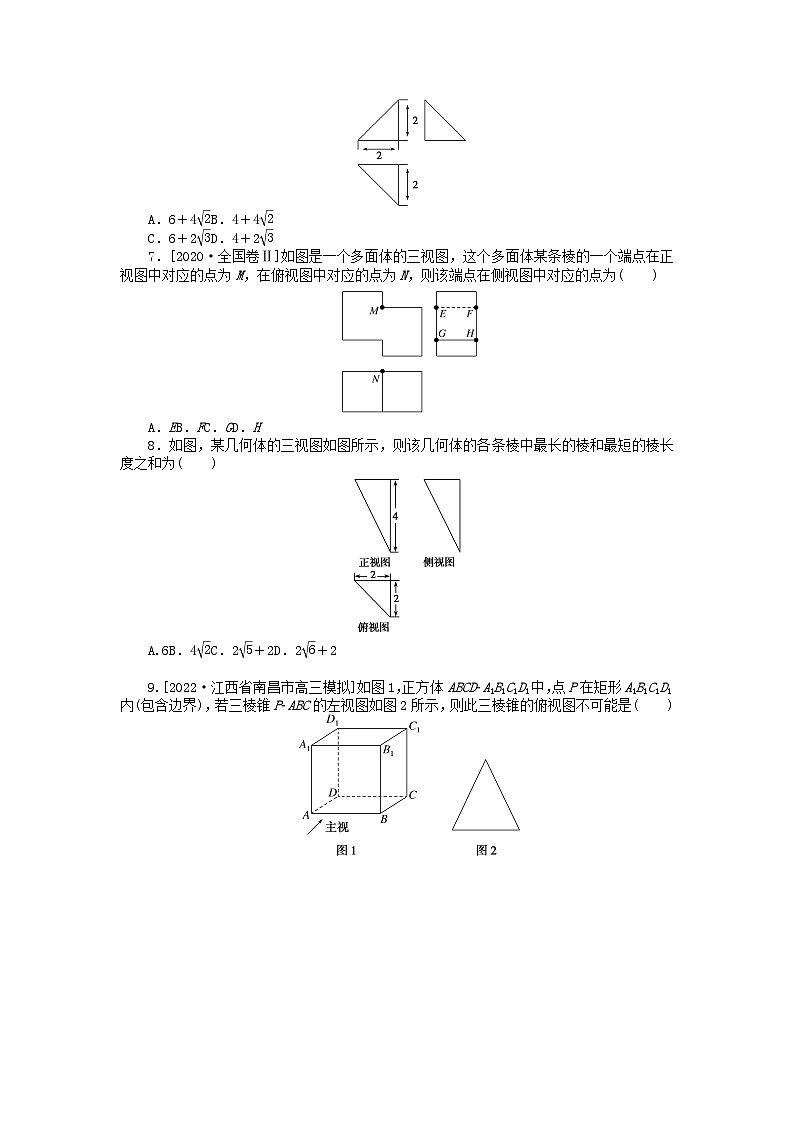
在一个正方体中，过顶点A的三条棱的中点分别为E，F，G.该正方体截去三棱锥A－EFG后，所得多面体的三视图中，正视图如图所示，则相应的侧视图是( )
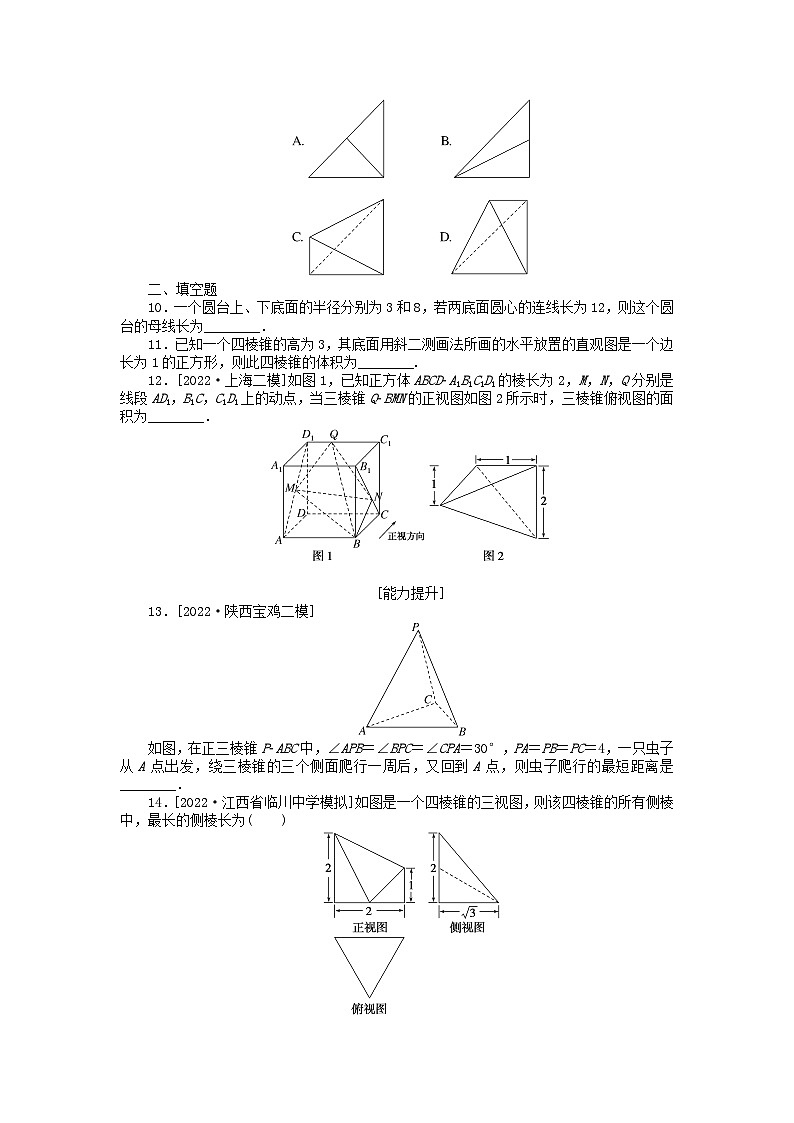
6．[2020·全国卷Ⅲ]如图为某几何体的三视图，则该几何体的表面积是( )
A．6＋4eq \r(2)B．4＋4eq \r(2)
C．6＋2eq \r(3)D．4＋2eq \r(3)
7．[2020·全国卷Ⅱ]如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M，在俯视图中对应的点为N，则该端点在侧视图中对应的点为( )
A．EB．FC．GD．H
8．如图，某几何体的三视图如图所示，则该几何体的各条棱中最长的棱和最短的棱长度之和为( )
A.6B．4eq \r(2)C．2eq \r(5)＋2D．2eq \r(6)＋2
9.[2022·江西省南昌市高三模拟]如图1，正方体ABCD­A1B1C1D1中，点P在矩形A1B1C1D1内(包含边界)，若三棱锥P­ABC的左视图如图2所示，则此三棱锥的俯视图不可能是( )
二、填空题
10．一个圆台上、下底面的半径分别为3和8，若两底面圆心的连线长为12，则这个圆台的母线长为________．
11．已知一个四棱锥的高为3，其底面用斜二测画法所画的水平放置的直观图是一个边长为1的正方形，则此四棱锥的体积为________.
12．[2022·上海二模]如图1，已知正方体ABCD­A1B1C1D1的棱长为2，M，N，Q分别是线段AD1，B1C，C1D1上的动点，当三棱锥Q­BMN的正视图如图2所示时，三棱锥俯视图的面积为________．
[能力提升]
13．[2022·陕西宝鸡二模]
如图，在正三棱锥P­ABC中，∠APB＝∠BPC＝∠CPA＝30°，PA＝PB＝PC＝4，一只虫子从A点出发，绕三棱锥的三个侧面爬行一周后，又回到A点，则虫子爬行的最短距离是________．
14．[2022·江西省临川中学模拟]如图是一个四棱锥的三视图，则该四棱锥的所有侧棱中，最长的侧棱长为( )
A．2B．eq \r(5)C．2eq \r(2)D．3
15．[2022·江西省景德镇高三质检]如图是一个四棱锥的三视图，则该四棱锥的所有侧面中，面积的最大值为________．
16．[2022·重庆一中高三月考]传说古希腊数学家阿基米德的墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等．这个“圆柱容球”是阿基米德生前最引以为豪的发现．如图，在底面半径为2的圆柱O1O2内有球O与圆柱O1O2的上、下底面及母线均相切，设A，B分别为圆柱O1O2的上、下底面圆周上一点，且O1A与O2B所成的角为90°，直线AB与球O的球面交于两点M，N，则线段MN的长度为________．
专练39 空间几何体的结构及其三视图和直观图
1．B 由圆台的定义可知①错误，②正确．对于命题③，只有平行于圆锥底面的平面截圆锥，才能得到一个圆锥和一个圆台，③不正确．
2．C 截面是任意的且都是圆面，则该几何体为球体．
3．D 如图所示的①②分别为△ABC的实际图与直观图
由斜二测画法可知：A′B′＝AB＝a，O′C′＝eq \f(1,2)OC＝eq \f(1,2)×a×eq \f(\r(3),2)＝eq \f(\r(3),4)a，
∴S△A′B′C′＝eq \f(1,2)A′B′×O′C′×sin45°＝eq \f(1,2)×a×eq \f(\r(3),4)a×eq \f(\r(2),2)＝eq \f(\r(6),16)a2.
4．D 由正视图与俯视图可得三棱锥A－BCD的一个侧面与底面垂直，其侧视图是直角三角形，且直角边长均为eq \f(\r(2),2)，故其侧视图的面积S＝eq \f(1,2)×eq \f(\r(2),2)×eq \f(\r(2),2)＝eq \f(1,4).
5．D 根据题目条件以及正视图可以得到该几何体的直观图，如图，结合选项可知该几何体的侧视图为D.
6．C 在正方体中还原几何体如图．
几何体为正方体的一部分：三棱锥P－ABC，
S表面积＝S△PAC＋S△PAB＋S△PBC＋S△BAC
＝eq \f(1,2)×2eq \r(2)×2eq \r(2)×eq \f(\r(3),2)＋eq \f(1,2)×2×2＋eq \f(1,2)×2×2＋eq \f(1,2)×2×2＝2eq \r(3)＋6.故选C.
7．A 根据三视图可得直观图如图所示，图中的点U在正视图中对应的点为M，在俯视图中对应的点为N，所以该端点在侧视图中对应的点为E.故选A.
8．D 由三视图知，该几何体是底面为腰长为2的等腰直角三角形、长为4的侧棱垂直于底面(垂足为腰与底边交点)的三棱锥，所以该三棱锥的最长棱的棱长为eq \r(42＋（2\r(2)）2)＝2eq \r(6)，最短棱的棱长为2，所以该几何体中最长的棱与最短的棱的长度之和为2eq \r(6)＋2，故选D.
9．D 如图(1)所示，若点P为A1D1的中点时，此时三棱锥P­ABC的俯视图为选项C；
如图(2)所示，若点P为B1C1的中点时，此时三棱锥P­ABC的俯视图为选项B；
如图(3)所示，取A1D1和B1C1的中点E和F，连接EF，若点P为EF的中点时，此时三棱锥P­ABC的俯视图为选项A；
所以此三棱锥P­ABC的俯视图不可能是选项D.
10．13
解析：如图，过A作AC⊥BO，交BO于点C，
则BC＝OB－O′A＝8－3＝5，
又AC＝12，
∴AB＝eq \r(AC2＋BC2)＝eq \r(52＋122)＝13.
11．2eq \r(2)
解析：∵该四棱锥底面的直观图是一个边长为1的正方形，故其直观图的面积为1，故原四棱锥的底面面积为2eq \r(2)，故其体积为V＝eq \f(1,3)S底h＝eq \f(1,3)×2eq \r(2)×3＝2eq \r(2).
12.eq \f(3,2)
解析：由题意得，点M为AD1的中点，点Q为C1D1中点，点N与B1重合，
∴其俯视图为三角形BM′N′，如图所示，
∴S＝eq \f(1,2)×eq \r(2)×eq \f(3\r(2),2)＝eq \f(3,2).
13．4eq \r(2)
解析：如图所示，将三棱锥的侧面展开，
因为∠APB＝∠BPC＝∠CPA＝30°，所以∠APA1＝90°，
当虫子沿AA1爬行时，距离最短，
又AA1＝eq \r(16＋16)＝4eq \r(2)，
所以虫子爬行的最短距离是4eq \r(2).
14．C
根据三视图还原原几何体的直观图如图所示：
由三视图可知△PAD为等腰三角形，AD＝2，PA＝PD＝eq \r(3＋（\f(AD,2)）2)＝2，
AB⊥平面PAD，PA⊂平面PAD，则AB⊥PA，AB＝1，CD＝2，
PB＝eq \r(PA2＋AB2)＝eq \r(5)，
同理可得PC＝eq \r(CD2＋PD2)＝2eq \r(2)，
由正视图可知，四边形ABCD为直角梯形，且AB、CD为腰，
BC＝eq \r(AD2＋（CD－AB）2)＝eq \r(5)，
因此，该四棱锥的所有侧棱中，最长的侧棱长为2eq \r(2).
15.eq \r(6)
解析：
由三视图可知，该几何体是如图所示四棱锥P­ABCD，
S△PCD＝eq \f(1,2)×2×2＝2，S△PAB＝eq \f(1,2)×2×1＝1，
S△PAD＝eq \f(\r(3),4)×22＝eq \r(3)，
PB＝BC＝eq \r(12＋22)＝eq \r(5)，PC＝eq \r(22＋22)＝2eq \r(2)，
所以S△PBC＝eq \f(1,2)×2eq \r(2)×eq \r(（\r(5)）2－（\r(2)）2)＝eq \f(1,2)×2eq \r(2)×eq \r(3)＝eq \r(6)，
所以侧面积的最大值为eq \r(6).
16．2eq \r(2)
解析：∵△OAO1≌△OBO2，∴OA＝OB，取AB中点G，连接OG，OA，OM，ON，OB，O2A，
∵OA＝OB，G为AB中点，∴OG⊥AB；
∵O2B⊥O1A，O2B⊥O1O2，O1A∩O1O2＝O1，O1A，O1O2⊂平面AO1O2，
∴O2B⊥平面AO1O2，又O2A⊂平面AO1O2，∴O2B⊥O2A；
∵OA2＝OO eq \\al(\s\up1(2),\s\d1(1)) ＋O1A2＝8，AB2＝O2A2＋O2B2＝22＋42＋22＝24，
∴OG＝eq \r(OA2－AG2)＝eq \r(8－6)＝eq \r(2)，
∴MG＝eq \r(OM2－OG2)＝eq \r(4－2)＝eq \r(2)，
∵OM＝ON，∴G也是MN中点，∴MN＝2MG＝2eq \r(2).