




冀教版九年级上册25.6 相似三角形的应用随堂练习题
展开试卷说明:本套试卷结合人教版数学九年级下册同步章节知识点,精选易错,常考,压轴类问题进行专题汇编!题目经典,题型全面,解题模型主要选取热点难点类型!同步复习,考前强化必备!适合成绩中等及偏上的学生拔高冲刺。
一、选择题:本大题共10小题,每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2分)(2023秋•海曙区校级期中)为了测量河宽AB,有如下方法:如图,取一根标尺CD横放,使CD∥AB,并使点B,D,O和点A,C,O分别在同一条直线上,量得CD=8米,OC=10米,AC=30米,则河宽AB的长度为( )米.
A.24B.30C.32D.40
2.(2分)(2023秋•东昌府区月考)如图是小孔成像原理的示意图,这支蜡烛在暗盒中所成的像CD的长是1cm,则像CD到小孔O的距离为( )
A.1cmB.2cmC.3cmD.4cm
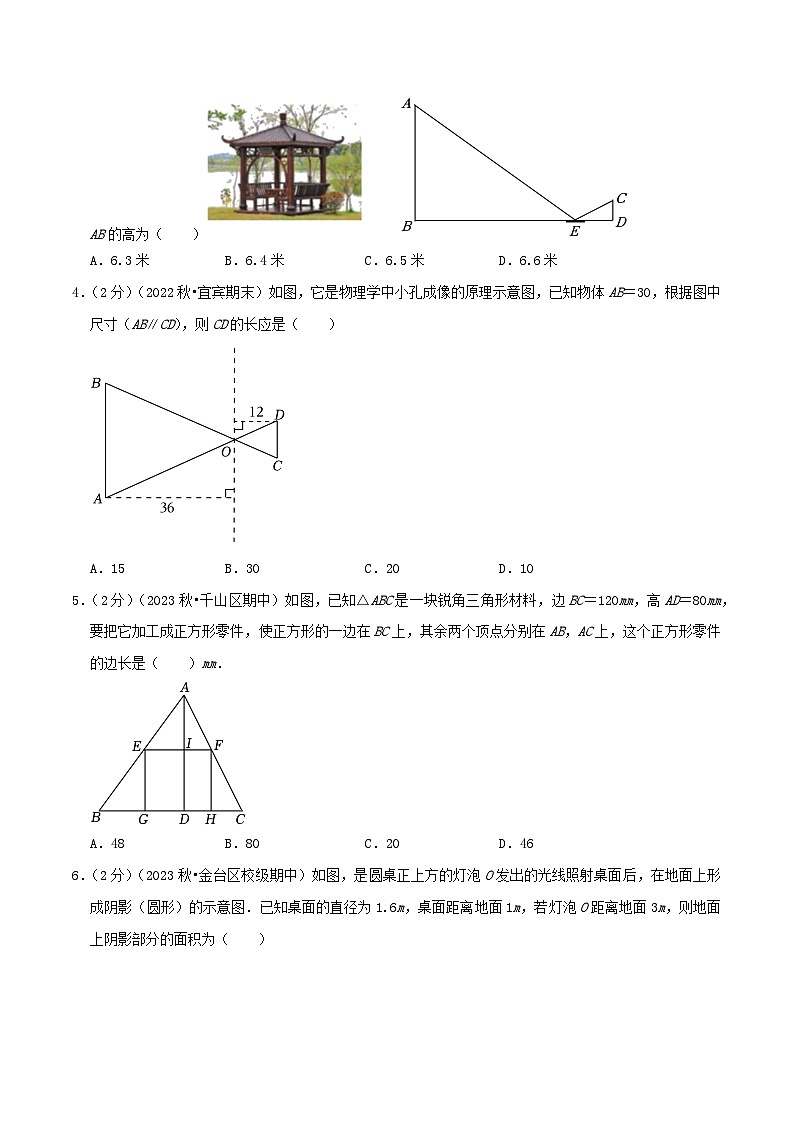
3.(2分)(2023秋•市北区期中)如图,某数学兴趣小组为了测量一凉亭AB的高度,他们采取了如下办法:①在凉亭的右边点E处放置了一平面镜,并测得BE=12米;②沿着直线BE后退到点D处,眼睛恰好看到镜子里凉亭的顶端A,并测得ED=3米,眼睛到地面的距离CD=1.6米(此时∠AEB=∠CED),那么凉亭AB的高为( )
A.6.3米B.6.4米C.6.5米D.6.6米
4.(2分)(2022秋•宜宾期末)如图,它是物理学中小孔成像的原理示意图,已知物体AB=30,根据图中尺寸(AB∥CD),则CD的长应是( )
A.15B.30C.20D.10
5.(2分)(2023秋•千山区期中)如图,已知△ABC是一块锐角三角形材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形零件的边长是( )mm.
A.48B.80C.20D.46
6.(2分)(2023秋•金台区校级期中)如图,是圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.6m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为( )
A.9.64πm2B.2.56πm2C.1.44πm2D.5.76πm2
7.(2分)(2023•白银二模)大约在两千四五百年前,墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是8cm,则蜡烛火焰的高度是( )cm.
A.B.6C.D.8
8.(2分)(2022秋•保定期末)如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=60cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,则树高AB为( )m.
A.5B.6.5C.7D.7.5
9.(2分)(2023春•招远市期末)如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中最大的“E”字高度为62.7mm,当测试距离为3m时,最大的“E”字高度为( )
A.37.62mmB.43mmC.43.62mmD.104.5mm
10.(2分)(2023春•芝罘区期末)操场上有一根竖直的旗杆AB,它的一部分影子(BC)落在水平地面上,另一部分影子(CD)落在操场的墙壁上,经测量,墙壁上的影高为1.2m,地面的影长为2.6m,同时测得一根高为2m的竹竿OM的影长是ON=1.6m,请根据以上信息,则旗杆的高度是( )
A.3.25mB.4.25mC.4.45mD.4.75m
二、填空题:本大题共10小题,每小题2分,共20分.
11.(2分)(2023•靖宇县一模)如图,为了测量一栋楼的高度,小王在他的脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到楼的顶部.如果小王身高1.55m,他的眼睛距地面1.50m,同时量得BC=0.3m,CE=2m,则楼高DE为 m.
12.(2分)(2023秋•朝阳区期中)据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第一个小孔成像的实验,阐释了光的直线传播原理,如图①所示.如图②所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是9cm,则蜡烛火焰的高度是 cm.
13.(2分)(2023秋•延庆区期中)如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=20cm,EF=10cm,测得边DF离地面的高度AC=1.5m,CD=6m,则树高AB是 m.
14.(2分)(2023•湖州)某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架(EF)放在离树(AB)适当距离的水平地面上的点F处,再把镜子水平放在支架(EF)上的点E处,然后沿着直线BF后退至点D处,这时恰好在镜子里看到树的顶端A,再用皮尺分别测量BF,DF,EF,观测者目高(CD)的长,利用测得的数据可以求出这棵树的高度.已知CD⊥BD于点D,EF⊥BD于点F,AB⊥BD于点B,BF=6米,DF=2米,EF=0.5米,CD=1.7米,则这棵树的高度(AB的长)是 米.
15.(2分)(2023•海州区一模)如图,某零件的外径为10cm,用一个交叉卡钳(两条尺长AC和BD相等)可测量零件的内孔直径AB.如果OA:OC=OB:OD=3,且量得CD=3cm,则零件的厚度x为 .
16.(2分)(2023春•南关区校级期末)明珠绿星数学社团想利用标杆测量楼高,小明先在N处竖立一根高1.6m的标杆MN,发现点B、M、P在同一直线上.测得PN=0.5m,AN=4.5m,已知,点A、N、P在同一直线上,MN⊥AP于点N,AB⊥AP于点A.则楼高AB为 m.
17.(2分)(2023秋•拱墅区校级月考)工人师傅在修茸一人字架屋顶BAC时需要加固,计划焊接三根钢条AD,DE,FG.在如图所示的△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,点E,F,G分别是AB,BD,AC上的点(如图中位置),连接DE,GF,交于点H,GF与AD交于点M,当H为FM的中点,BF:CF=1:5,AG:AE=5:7 时,= ,△AGM的面积为 .
18.(2分)(2022秋•西安期末)《九章算术》中记载着这样的一个问题:“今有邑方,不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何?”大意如下:如图,M、N为正方形ABCD一组对边的中点,△GEF中,G、M、N、E四点共线,∠E=90°,F、A、G三点共线,且AD⊥GE,GM=20,NE=14,EF=1775,设正方形ABCD的边长为x,请根据题意列方程,并将方程整理成一元二次方程的一般形式: .
19.(2分)(2023春•柯桥区期末)母亲节,小敏准备送礼物给妈妈,他用正方形纸板,制作一个正方体礼品盒(如图所示裁剪).已知正方形纸板边长为10分米,则这个礼品盒的边长 分米.
20.(2分)(2021秋•高新区校级期末)中国是礼仪之邦.从西四环下高速时,小明看到高新区的门户——“礼仪之门”这个雕塑,他想利用所学的数学知识测量它的高度.他在点C处放一镜子,并作一标记,来回走动,走到点D时,看到“礼仪之门”顶点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度ED=1.5米,CD=2米.然后,小明从点D沿DH方向走了19米,到达“礼仪之门”影子的末端G处,此时,测得小明身高FG=1.6米,影长GH=3.2米,则“礼仪之门”的高AB为 米.
三、解答题:本大题共8小题,21-22题每小题6分,23-28题每小题8分,共60分.
21.(6分)(2022秋•南康区校级期末)如图1,小红家的阳台上放置了一个晒衣架,图2是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点在地面上,经测量得到AB=CD=136cm,OA=OC=51cm,OE=OF=34cm,现将晒衣架完全稳固张开,扣链EF成一条线段.
(1)连接AC.求证:AC∥EF;
(2)若EF=32cm,求利用夹子垂挂在晒衣架上的连衣裙总长度小于多少时,连衣裙才不会拖在地面上?
22.(6分)(2023•碑林区校级一模)如图,小明用自制的直角三角形纸板DEF测量水平地面上树AB的高度,已知两直角边EF:DE=2:3,他调整自己的姿势和三角形纸板的位置,使斜边DF保持水平,并且边DE与点B在同一直线上,DM垂直于地面,测得AM=21m,边DF离地面的距离为1.6m,求树高AB.
23.(8分)(2023秋•雁塔区校级月考)在物理学中我们学过光的反射定律.数学综合实践小组想利用光的反射定律测量池塘对岸一棵树的高度AB,测量步骤如下:
①如图,在地面上的点C处放置一块平面镜(镜子大小忽略不计),小华站在BC的延长线上,当小华从平面镜中刚好看到树的顶点A时,测得小华到平面镜的距离CD=2米,小华的眼睛E到地面的距离ED=1.5米;
②将平面镜从点C沿BC的延长线移动10米到点F处,小华移动到点H处时,小华的眼睛G又刚好在平面镜中看到树的顶点A,这时测得小华到平面镜的距离FH=3米.
请根据以上测量过程及数据求出树的高度AB.
24.(8分)(2023秋•封丘县月考)2022年9月16日,第九批在韩中国人民志愿军烈士遗骸归国.七十多年前,志愿军战士们义无反顾地用血肉之躯把祖国护卫在身后,把炮火挡在了国门之外.面对敌人精良的武器,志愿军战士经常使用一些土办法来反击敌人,其中“跳眼法”就是炮兵常用的一种简易测距方法(图1),结合相似三角形原理和光的直线传播原理,可以计算出被测物的大致距离.如图2,点A为左眼,点B为右眼,点O为右手大拇指,点C为敌人的位置,点D为敌人正左侧方的某一个参照物(CD∥AB),目测CD的长度后,就可以计算C处敌人距离我方的大致距离.已知大多数人的双眼距离约为6.4厘米,而手臂长约64厘米.若CD的估测长度为50米,那么CO的大致距离为多少米?
25.(8分)(2023秋•西安期中)为了测量学校旗杆上旗帜的宽度MN,如图,点P、G.C、A在同一水平直线上,MG⊥PA,小红在C处竖立一根标杆BC(BC⊥PA),地面上的点A、标杆顶端B和点N在一条直线上(N在MG上),BC=1.5米,AC=1米,AG=8米;小明手持自制直角三角纸板DEF(DF⊥EF),其中EF=0.1米,DF=0.2米,使长直角边DF与水平地面平行,调整位置,恰好在P点时点D、E、M在一条直线上,DP⊥PA,DP=1.5米,PG=23.6米,请你根据上述信息求出旗帜的宽度MN.
26.(8分)(2023•长安区校级一模)如图①,“丝绸之路群雕”刻画和表达了一队来往于丝路中途的中外混合的骆驼商旅,已成为西安著名的城市标志之一.为了测量群雕某处的高度AB,小明和晓璐带着平面镜和皮尺去进行测量.测量过程如下:如图②,首先,小明在M处放置了一面平面镜,然后沿BM后退,当小明蹲在点D处时恰好能在平面镜中看到雕塑顶端A的像,此时小明的眼睛到地面的距离CD=0.7米,MD=0.5米;然后小明在D处起立站直,晓璐眼睛贴地观察发现地面上点F、小明头顶E和顶端A重合,测得小明的身高DE=1.5米,DF=1.5米,AB⊥BF,DE⊥BF,点B、M、D、F在同一条水平线上,点C在DE上,请你求出该处雕塑的高AB.(平面镜的大小、厚度忽略不计,晓璐眼睛贴地观察时眼睛到地面的距离忽略不计)
27.(8分)(2023秋•姑苏区校级月考)要在半径长为1米、圆心角为60°的扇形AOB铁皮上截取一块尽可能大的正方形.小明设计如下两种截取方案.
方案一(如图1):C在半径OA上,D、E在半径OB上,F在弧AB上;
方案二(如图2):C在OA上,D在OB上,E,F在弧AB上.
请通过计算这两种方案中正方形铁皮的面积帮小明选择合理的方案.(参考数据:)
28.(8分)(2023秋•昌平区期中)为了测量水平地面上一栋建筑物AB的高度,学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:先在水平地面上放置一面平面镜,并在镜面上做标记点C,后退至点D处恰好看到建筑物AB的顶端A在镜子中的像与镜面上的标记点C重合,法线是FC,小军的眼睛与地面距离DE是1.65m,BC、CD的长分别为60m、3m,求建筑物AB的高度.
初中数学冀教版九年级上册27.3 反比例函数的应用练习题: 这是一份初中数学冀教版九年级上册<a href="/sx/tb_c41519_t7/?tag_id=28" target="_blank">27.3 反比例函数的应用练习题</a>,文件包含专题04反比例函数的应用专项培优训练教师版docx、专题04反比例函数的应用专项培优训练学生版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
初中数学冀教版九年级上册27.2 反比例函数的图像和性质同步训练题: 这是一份初中数学冀教版九年级上册<a href="/sx/tb_c41518_t7/?tag_id=28" target="_blank">27.2 反比例函数的图像和性质同步训练题</a>,文件包含专题01反比例函数的图像和性质专项培优训练教师版docx、专题01反比例函数的图像和性质专项培优训练学生版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
冀教版九年级上册27.1 反比例函数课堂检测: 这是一份冀教版九年级上册<a href="/sx/tb_c41517_t7/?tag_id=28" target="_blank">27.1 反比例函数课堂检测</a>,文件包含专题02反比例函数系数k的几何意义专项培优训练教师版docx、专题02反比例函数系数k的几何意义专项培优训练学生版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。













