人教版八年级上册14.2.2 完全平方公式课时训练

这是一份人教版八年级上册14.2.2 完全平方公式课时训练，文件包含2024年中考道德与法治一轮复习知识清单全国通用-专题03多边形及其内角和专项培优训练教师版docx、2024年中考道德与法治一轮复习知识清单全国通用-专题13完全平方公式和平方差公式的几何背景专项培优训练教师版docx、2024年中考道德与法治一轮复习知识清单全国通用-专题13完全平方公式和平方差公式的几何背景专项培优训练学生版docx等3份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。

试卷说明：本套试卷结合人教版数学八年级上册同步章节知识点，精选易错，常考，压轴类问题进行专题汇编！题目经典，题型全面，解题模型主要选取热点难点类型！同步复习，考前强化必备！适合成绩中等及偏上的学生拔高冲刺。
一、选择题：本大题共10小题，每小题2分，共20分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．（2分）（2023秋•东城区校级期中）有两个正方形A，B，现将B放在A的内部如图甲，将A，B并排放置后构造新的正方形如图乙，若图甲和图乙中阴影部分的面积分别为4和52，则正方形A，B的面积之和为（ ）
A．48B．56C．64D．72
解：设正方形A的边长为x，B的边长为y，
由图甲和图乙中阴影部分的面积分别为4和52，可列方程组为，
将②化简，得2xy＝52③，
由①得x2+y2﹣2xy＝4，将③代入可得x2+y2＝56．
故选：B．
2．（2分）（2022秋•离石区期末）在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪拼成一个矩形（如图），通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（ ）
A．a2﹣ab＝a（a﹣b）B．a2﹣b2＝（a+b）（a﹣b）
C．（a+b）2＝a2+2ab+b2D．（a﹣b）2＝a2﹣2ab+b2
解：由图可知，大正方形减小正方形剩下的部分面积为a2﹣b2；
拼成的长方形的面积：（a+b）×（a﹣b），
所以得出：a2﹣b2＝（a+b）（a﹣b），
故选：B．
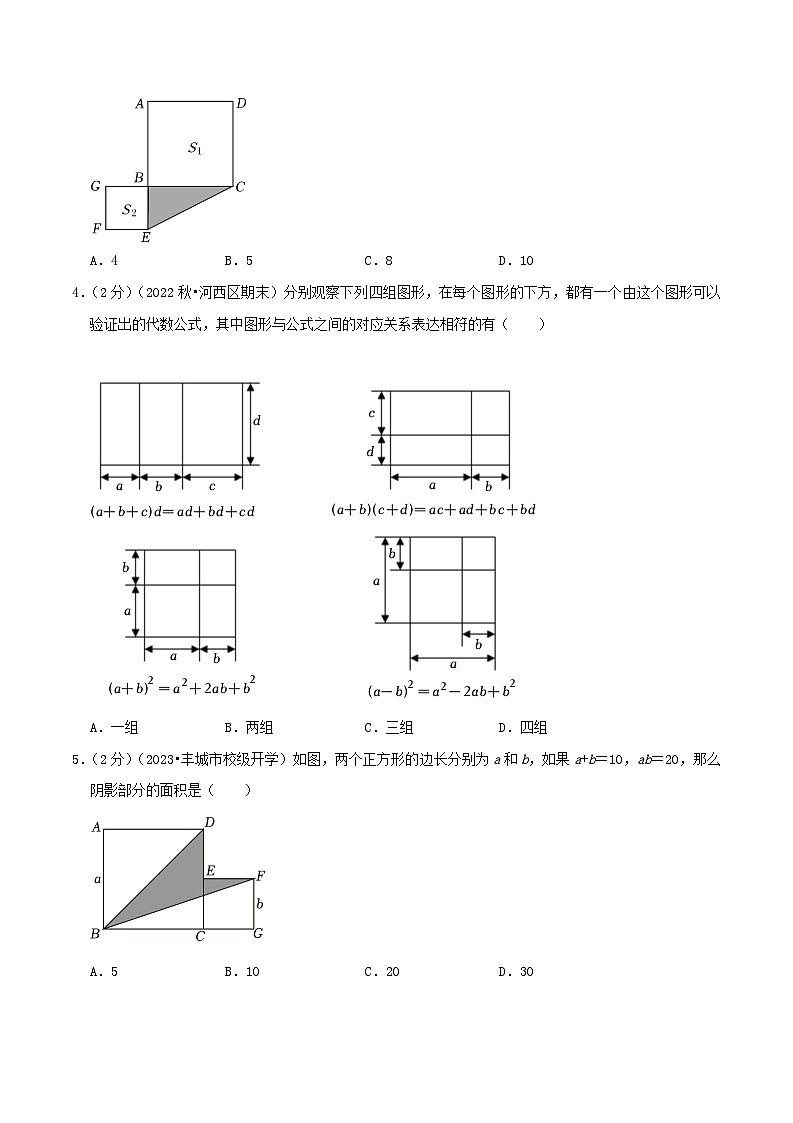
3．（2分）（2022秋•邻水县期末）如图，点B是线段CG上一点，以BC，BG为边向两边作正方形，面积分别是S1和S2，设CG＝6，两个正方形的面积之和S1+S2＝16，则阴影部分△BCE的面积为（ ）
A．4B．5C．8D．10
解：设BC＝a，BE＝b，
∵四边形BEFG是正方形，
∴BE＝BG＝b，
∵两正方形的面积和S1+S2＝16，
∴a2+b2＝16，
∵a+b＝6，
∴（a+b）2＝a2+b2+2ab＝36，
∴ab＝10，
∴S阴＝ab＝5，
故选：B．
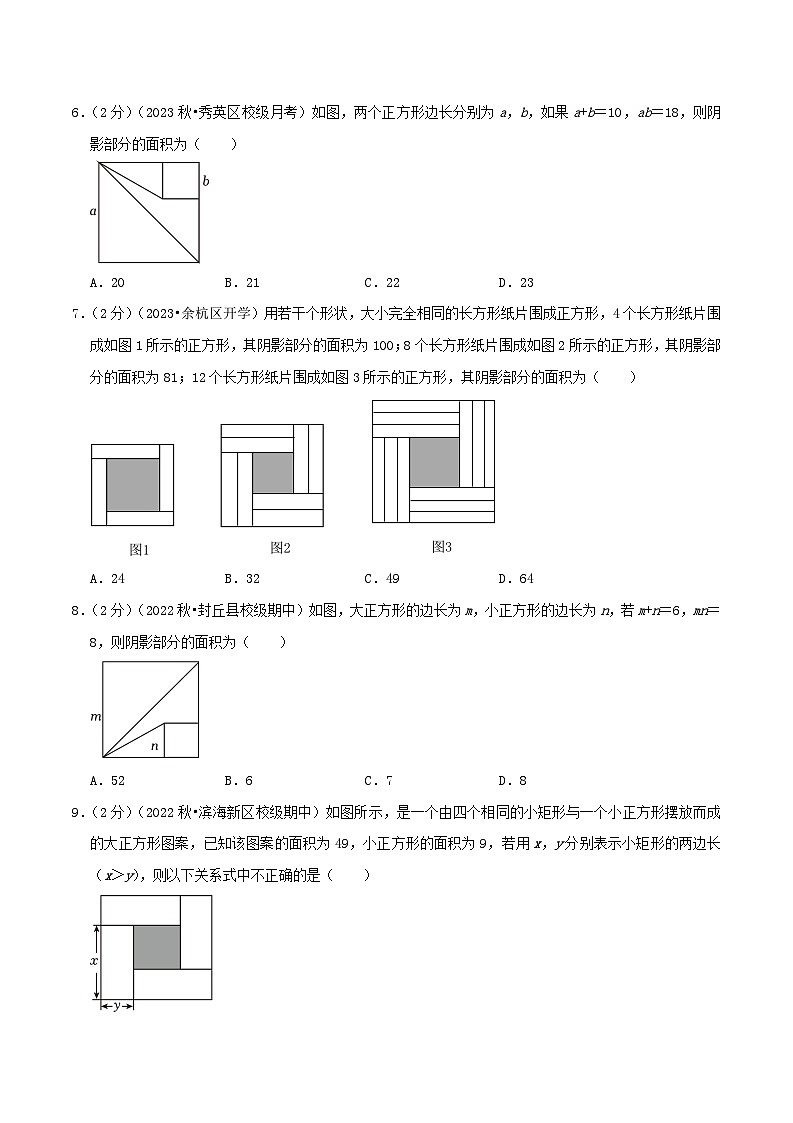
4．（2分）（2022秋•河西区期末）分别观察下列四组图形，在每个图形的下方，都有一个由这个图形可以验证出的代数公式，其中图形与公式之间的对应关系表达相符的有（ ）
A．一组B．两组C．三组D．四组
解：图1，整体长方形的长为a+b+c，宽为d，因此面积为（a+b+c）d，
整体长方形由三个长方形构成的，这三个长方形的面积和为ad、bd、cd，
所以有：（a+b+c）d＝ad+bd+cd，
因此图1符合题意；
图2，整体长方形的长为a+b，宽为c+d，因此面积为（a+b）（c+d），
整体长方形由四个长方形构成的，这四个长方形的面积和为ac+ad+bc+bd，
所以有：（a+b）（c+d）＝ac+ad+bc+bd，
因此图2符合题意；
图3，整体正方形的边长为a+b，因此面积为（a+b）2，
整体正方形由四个部分构成的，这四个部分的面积和为a2+2ab+b2，
所以有：（a+b）2＝a2+2ab+b2，
因此图3符合题意；
图4，整体正方形的边长为a，因此面积为a2，
整体正方形由四个部分构成的，其中较大的正方形的边长为a﹣b，因此面积为（a﹣b）2，较小正方形的边长为b，因此面积为b2，
另外两个长方形的长为（a﹣b），宽为b，则面积为（a﹣b）×b×2＝2ab﹣2b2，
所以有a2＝（a﹣b）2+b2+2ab﹣2b2，
即（a﹣b）2＝a2﹣2ab+b2，
因此图4符合题意；
综上所述，四组均符合题意；
故选：D．
5．（2分）（2023•丰城市校级开学）如图，两个正方形的边长分别为a和b，如果a+b＝10，ab＝20，那么阴影部分的面积是（ ）
A．5B．10C．20D．30
解：根据题意可得，阴影部分面积为两个正方形面积和减去空白面积，
即（a2+b2）﹣﹣＝（a2+b2﹣ab）＝（a2+b2+2ab﹣3ab）＝[（a+b）2﹣3ab]；
代入a+b＝10，ab＝20可得：
S阴影面积＝（10×10﹣20×3）÷2＝20．
故选：C．
6．（2分）（2023秋•秀英区校级月考）如图，两个正方形边长分别为a，b，如果a+b＝10，ab＝18，则阴影部分的面积为（ ）
A．20B．21C．22D．23
解：阴影面积＝大正方形﹣大三角形面积﹣小三角形面积，
＝a2﹣a2﹣b（a﹣b）
＝a2+b2﹣ab
＝（a2+b2﹣ab）
＝（a2+b2+2ab﹣2ab﹣ab）
＝[（a+b）2﹣3ab]
＝×（100﹣54）
＝23
故答案为：D．
7．（2分）（2023•余杭区开学）用若干个形状，大小完全相同的长方形纸片围成正方形，4个长方形纸片围成如图1所示的正方形，其阴影部分的面积为100；8个长方形纸片围成如图2所示的正方形，其阴影部分的面积为81；12个长方形纸片围成如图3所示的正方形，其阴影部分的面积为​（ ）
A．24B．32C．49D．64
解：因为图1中阴影部分的面积是100，
所以阴影正方形的边长为10．
同理图2中阴影正方形的边长为9．
设小长方形的长为x，宽为y，
则，解得．
所以小长方形的长为11，宽为1．
又图3中阴影正方形的边长为：x﹣3y＝11﹣3＝8，
所以图3中阴影正方形的面积为：82＝64．
故选：D．
8．（2分）（2022秋•封丘县校级期中）如图，大正方形的边长为m，小正方形的边长为n，若m+n＝6，mn＝8，则阴影部分的面积为（ ）
A．52B．6C．7D．8
解：m2﹣m2﹣n（m﹣n）＝m2﹣n2＝（m2+2mn+n2﹣2mn﹣mn）＝[（m+n）2﹣3mn]，
把m+n＝6，mn＝8代入得：×（62﹣3×8）＝6，
故选：B．
9．（2分）（2022秋•滨海新区校级期中）如图所示，是一个由四个相同的小矩形与一个小正方形摆放而成的大正方形图案，已知该图案的面积为49，小正方形的面积为9，若用x，y分别表示小矩形的两边长（x＞y），则以下关系式中不正确的是（ ）
A．x+y＝7B．x﹣y＝3C．4xy+9＝49D．x2+y2＝25
解：∵该图案的面积为49，
∴正方形图案的边长7，同时还可用（x+y）来表示，
∴x+y＝7，A选项正确，不符合题意；
∵小正方形的面积为9，
∴小正方形图案的边长3，同时还可用（x﹣y）来表示，
∴x﹣y＝3，B选项正确，不符合题意；
∵正方形图案面积从整体看是49，从组合来看，可以是（x+y）2，还可以是（4xy+9），
∴（x+y）2＝x2+y2+2xy＝49＝4xy+9，C选项正确，不符合题意；
∴xy＝10，
∴x2+y2＝29，D选项错误，符合题意；
故选：D．
10．（2分）（2022秋•西区期中）如图①所示，在变成为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪拼成一个②所示的矩形，通过计算两个图形阴影部分的面积，验证了一个等式，这个等式是（ ）
A．a2﹣b2＝（a+b）（a﹣b）B．（a+b）（a﹣b）＝a2﹣b2
C．（a+b）2＝a2+2ab+b2D．（a﹣b）2＝a2﹣2ab+b2
解：图①中阴影部分的面积为：a2﹣b2，
图②中阴影部分的面积为：（a+b）（a﹣b）．
又两个阴影部分的面积是相等的，
则a2﹣b2＝（a+b）（a﹣b）．
故选：A．
二．填空题（共10小题，满分20分，每小题2分）
11．（2分）（2023秋•尤溪县月考）如图，C是线段AB上的一点，以AC，BC为边在AB的两侧作正方形，设AB＝8，两个正方形的面积和为40，即S1+S2＝40，则图中阴影部分的面积为 6 ．
解：设AC＝a，BC＝b，由题意可知，a+b＝AC+BC＝AB＝8，a2+b2＝S1+S2＝40，
∵（a+b）2＝a2+2ab+b2，
∴ab＝
＝
＝12，
∴S阴影部分＝ab＝6，
故答案为：6．
12．（2分）（2022秋•细河区期末）如图1，将边长为x的大正方形剪去一个边长为1的小正方形（阴影部分），并将剩余部分沿虚线剪开，得到两个长方形，再将这两个长方形拼成图2所示长方形．这两个图能解释一个等式是 x2﹣1＝（x+1）（x﹣1） ．
解：图1的面积为：x2﹣1，拼成的图2的面积为：（x+1）（x﹣1），
所以x2﹣1＝（x+1）（x﹣1），
故答案为：x2﹣1＝（x+1）（x﹣1）．
13．（2分）（2022秋•湖里区期末）在一个面积为36cm2正方形纸板中剪下边长为acm大正方形和边长为bcm的小正方形（如图1），再在大正方形沿一个顶点剪下一个边长为bcm的小正方形（如图2），得到一个周长为16cm的六边形ABCDEF，则原大正方形中剩下的两个长方形的面积和为 16 cm2．
解：由题意得，
解得或（舍去），
∴原大正方形中剩下的两个长方形的面积和为：4×2×2＝16，
故答案为：16．
14．（2分）（2023春•雁塔区校级月考）如图，两个正方形的边长分别为a，b（a＞b），若a+b＝6，ab＝6，则图中阴影部分的面积为 6 ．
解：∵阴影的面积＝△ABC的面积﹣△AFD的面积﹣△BEF的面积﹣△DCE的面积，
∴阴影的面积＝a2﹣（a﹣b）b﹣（a﹣b）b﹣b2＝（a2+b2）﹣ab＝（a+b）2﹣2ab，
∵a+b＝6，ab＝6，
∴阴影的面积＝×62﹣2×6＝6．
故答案为：6．
15．（2分）（2022秋•密云区期末）在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图），把余下的部分拼成一个矩形（如图），根据两个图形中阴影部分的面积相等，可以验证的乘法公式是 （a+b）（a﹣b）＝a2﹣b2 ．
解：阴影部分的面积＝（a+b）（a﹣b）＝a2﹣b2；
因而可以验证的乘法公式是（a+b）（a﹣b）＝a2﹣b2．
16．（2分）（2021秋•凤凰县期末）如图，将大正方形通过剪、割、拼后分解成新的图形，利用等面积法可证明某些乘法公式，在给出的4幅拼法中，其中能够验证平方差公式的有 1，2，3 （填序号，多选）．
解：在图1中，4个梯形的面积相等，左边4个梯形的面积＝a2﹣b2，右边4个梯形的面积＝（a+b）（a﹣b）．可得：a2﹣b2＝（a+b）（a﹣b），可以验证平方差公式；
在图2中，图形面积＝a2﹣b2＝a（a﹣b）+b（a﹣b）＝（a+b）（a﹣b），可以验证平方差公式；
在图3中，2个直角梯形的面积相等，左边2个直角梯形的面积＝a2﹣b2，右边2个直角梯形的面积＝（2b+2a）•（a﹣b）＝（a+b）（a﹣b），可得：a2﹣b2＝（a+b）（a﹣b），可以验证平方差公式；
在图4中，四边形的面积＝（a+b）2，也可以表示为：4ab+（a﹣b）2，即（a+b）2＝4ab+（a﹣b）2＝a2+2ab+b2，可以验证完全平方公式，不可验证平方差公式；
故答案为：1，2，3．
17．（2分）（2023春•潍坊期末）如图，两个正方形的边长分别为a和b，其中B，C，G三点在同一直线上，若a+b＝20，ab＝80，那么阴影部分的面积等于 120 ．
​
解：由图可知：
S五边形ABGFD＝S正方形ABCD+S梯形DCGF
＝
＝，
∴S阴影＝S五边形ABGFD﹣S△ABD﹣S△BCF
＝
＝
＝，
∵a+b＝20，ab＝80，
∴a2+b2＝（a+b）2﹣2ab＝202﹣2×80＝240，
∴，
故答案为：120．
18．（2分）（2023•青羊区校级开学）（1）若m+n＝3，m2+n2＝25，求mn的值；
（2）如图，点E、F分别是正方形ABCD的边AD与AB上的点，以AE、AF为边在正方形内部作面积为8的长方形AFGE，再分别以FG、EG为边作正方形FGPH和正方形GRQE．若图中阴影部分的面积为20，求长方形AFGE的周长．
解：（1）因为（m+n）2＝m2+2mn+n2，
所以mn＝．
又m+n＝3，m2+n2＝25，
所以mn＝．
即mn的值为﹣8．
（2）设长方形AFGE的长和宽为分别为x和y，
根据题意得，
所以（x+y）2
＝x2+2xy+y2
＝20+2×8
＝36，
则x+y＝6，
故2（x+y）＝12．
所以长方形AFGE的周长为12．
19．（2分）（2021秋•平泉市期末）如图1，将长方形纸片沿图中虚线剪成四个形状和大小相同的小长方形，然后拼成如图2的一个大正方形．
（1）若图1中大长方形的长为4，宽为2，则图2中小正方形（阴影部分）的面积S＝ 1 ；
（2）若图1中大长方形的长为2m，宽为2n，则图2中小正方形（阴影部分）的面积S＝ m2+n2﹣2mn （用含m、n的式子表示）．
解：（1）图2中小正方形（阴影部分）的面积S＝（2﹣1）2＝1，
故答案为：1；
（2）图2中小正方形（阴影部分）的面积S＝（m﹣n）2＝m2+n2﹣2mn，
故答案为：m2+n2﹣2mn．
20．（2分）（2022秋•自流井区校级期末）如图，从边长为（a+5）cm的正方形纸片中剪去一个边长为（a+2）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个长方形（不重叠无缝隙），则长方形的面积为 （6a+21） cm2．
解：根据题意，长方形的面积为：
[（a+5）+（a+2）][（a+5）﹣（a+2）]
＝3（2a+7）
＝6a+21，
故答案为：6a+21．
三、解答题：本大题共8小题，21-22题每小题6分，23-28题每小题8分，共60分．
21．（6分）（2023春•岑溪市期末）从边长为a的正方形减掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．
（1）上述过程所揭示的乘法公式是 a2﹣b2＝（a+b）（a﹣b） ．
（2）若9x2﹣16y2＝30，3x+4y＝6，求3x﹣4y的值．
（3）计算：．
解：（1）上述过程所揭示的乘法公式是a2﹣b2＝（a+b）（a﹣b）
（2）9x2﹣16y2＝30
∴（3x+4y）（3x﹣4y）＝30
∵3x+4y＝6
∴3x﹣4y＝5
（3）原式＝
＝
＝
＝
22．（6分）（2023春•西湖区期末）已知实数x，y满足：x+y＝7，xy＝12．
（1）求x2+y2的值；
（2）将长方形ABCD和长方形CEFG按照如图方式放置，其中B，C，G三点在同一条直线上，点E在x边CD上，连接BD，BF，已知AD＝x，AB＝nx，FG＝y，EF＝ny，阴影部分的面积为14，求n的值．
解：（1）∵x+y＝7．xy＝12．
∴x2+y2+2xy＝49，
∴x2+y2＝49﹣2×12＝25．
（2）由图示可知，阴影部分的面积等于长方形ABCD面积的一半加长方形CEFG的面积减去△BGF的面积，
即S阴＝nx2+ny2﹣y（x+ny）＝14．
整理得：n（x2+y2）﹣xy＝14，
∴n×25﹣×12＝14，
解得n＝．
23．（8分）（2023春•承德期末）如图1，两个边长为a和b的正方形如图摆放，其阴影面积为S1；
如图2，两个边长为b的正方形和一个边长为a的正方形如图摆放，其阴影面积为S2；
如图3，两个边长为a和b的正方形如图摆放，其阴影面积为S3；
解答问题：
①用含a、b的代数式分别表示S1、S2；
②若a+b＝10，ab＝22，求S1+S2的值；
③当S1+S2＝32时，求图3中阴影部分的面积S3．
解：①如图（1），阴影部分可以看作两个正方形的面积差，即S1＝a2﹣b2；
图（2）中，阴影部分的面积为2个边长为b的正方形的面积减去于个长为a宽为b的长方形的面积，即S2＝2b2﹣ab；
②∵a+b＝10，ab＝22，
∴S1+S2＝a2﹣b2+2b2﹣ab
＝a2+b2﹣ab
＝（a+b）2﹣3ab
＝100﹣66
＝34；
③如图（3），阴影部分的面积S3＝a2+b2﹣a2﹣b（a+b）
＝a2+b2﹣ab
＝（a2+b2﹣ab），
∵S1+S2＝32，即a2+b2﹣ab＝32，
∴S3＝×32＝16．
24．（8分）（2022秋•洪山区期末）（1）用边长分别为a，b的两个正方形和长宽分别为a，b的两个长方形按如图摆放可拼成一个大正方形，用两种不同的方法可以表示图中阴影部分的面积和．
请你用一个等式表示（a+b）2，a2+b2，ab之间的数量关系 a2+b2＝（a+b）2﹣2ab ．
（2）根据（1）中的数量关系，解决如下问题：
①已知m+n＝6，m2+n2＝26，求m﹣n的值；
②已知（x﹣2021）2+（x﹣2023）2＝74，求（x﹣2022）2的值．
解：（1）方法一：阴影部分是两个正方形的面积和，即a2+b2；
方法二：阴影部分也可以看作边长为（a+b）的面积，减去两个长为a，宽为b的长方形面积，即（a+b）2﹣2ab，
由两种方法看出a2+b2＝（a+b）2﹣2ab，
故答案为：a2+b2＝（a+b）2﹣2ab；
（2）①∵m+n＝6，
∴（m+n）2＝36＝m2+2mn+n2，
∵m2+n2＝26，
∴2mn＝10，
即mn＝5；
∴（m﹣n）2＝m2﹣2mn+n2＝26﹣10＝16，
∴m﹣n＝±4；
②设a＝x﹣2021，b＝x﹣2023，
则a﹣b＝2，a2+b2＝（x﹣2021）2+（x﹣2023）2＝74，
∴，
即（x﹣2021）（x﹣2023）＝35，
∴[（x﹣2022）+1][（x﹣2022）﹣1]＝（x﹣2022）2﹣1＝35，
∴（x﹣2022）2＝36．
25．（8分）（2023春•汨罗市期中）如图1是一个长为4a，宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成如图2的正方形．
（1）由图2可以直接写出（a+b）2，（a﹣b）2，ab之间的一个等量关系是 （a+b）2＝（a﹣b）2+4ab ．
（2）根据（1）中的结论，解决下列问题：3x+4y＝10，xy＝2，求3x﹣4y的值；
（3）两个正方形ABCD，AEFG如图3摆放，边长分别为x，y．若x2+y2＝34，BE＝2，求图中阴影部分面积和．
解：（1）∵大正方形的面积等于4个小长方形和小正方形面积之和，
∴（a+b）2＝4ab+（b﹣a）2．
∴（a+b）2＝（a﹣b）2+4ab．
故答案为：（a+b）2＝（a﹣b）2+4ab．
（2）由（1）得：
（3x+4y）2＝（3x﹣4y）2+4×3x×4y．
∴（3x﹣4y）2＝（3x+4y）2﹣48xy
∴（3x﹣4y）2＝100﹣96＝4．
∴3x﹣4y＝±2．
（3）∵ABCD，AEFG为正方形，边长分别为x，y．BE＝2，
∴DG＝BE＝2，x﹣y＝2．
∴（x﹣y）2＝4．
∴x2﹣2xy+y2＝4．
∵x2+y2＝34，
∴2xy＝30．
∴x2+2xy+y2＝34+30，
∴（x+y）2＝64．
∵x＞0，y＞0，
∴x+y＝8．
∴＝y+x＝8．
26．（8分）（2023春•靖江市期末）完全平方公式经过适当的变形，可以解决很多数学问题．
例如：若a+b＝3，ab＝1，求 a2+b2 的值．
解：∵a+b＝3，ab＝1，
∴（a+b）2＝9，2ab＝2．
∴a2+b2+2ab＝9，
∴a2+b2＝7．
根据上面的解题思路与方法解决下列问题：
（1）若m+n＝3，mn＝1，则 （m﹣n）2＝ 5 ；
（2）如图，C是线段AB上的一点，分别以AC，BC为边向两侧作正方形BCFG与正方形ACDE，设AB＝6，两正方形的面积和为20，求△AFC的面积．
解：（1）∵m+n＝3，mn＝1，
∴（m+n）2＝9，2mn＝2．
∴m2+n2+2mn＝9，
∴m2+n2＝7，
∴（m﹣n）2＝m2+n2﹣2mn＝7﹣2＝5；
故答案为：5．
（2）设正方形BCFG与正方形ACDE的边长分别为m，n，
∵AB＝6，
∴m+n＝6，
∵两正方形的面积和为20，
∴m2+n2＝20，
∵（m+n）2＝36，
∴m2+n2+2mn＝36，
∴20+2mn＝36，
∴mn＝8，
∴△AFC的面积＝mn＝×8＝4．
27．（8分）（2023春•临泉县期末）有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：
善于观察思考的小明发现：利用图形面积关系这三种方案都能验证公式：a2+2ab+b2＝（a+b）2．
对于方案一，小明是这样验证的：
因为大正方形的面积可以看成：a2+ab+ab+b2＝a2+2ab+b2，又可以看成（a+b）2，所以a2+2ab+b2＝（a+b）2．
解答下列问题：
（1）公式验证：请根据方案二、方案三，分别写出公式的验证过程．
方案二： （a+b）2＝a2+ab+b（a+b）＝a2+2ab+b2 ；
方案三： （a+b）2＝a2+2×（a+a+b）•b＝a2+2ab+b2 ；
（2）公式应用，已知实数a，b均为正数，且a﹣b＝2，ab＝3，求a+b的值．
解：（1）方案二：
∵大正方形是由一个小正方形面积和两个矩形组成，
∴大正方形的面积为：a2+ab+b（a+b）＝a2+2ab+b2，
又∵大正方形的边长为（a+b），
∴大正方形的面积为：（a+b）2，
∴（a+b）2＝a2+2ab+b2；
方案三：
∵大正方形是由一个小正方形面积和两个直角梯形组成，
∴大正方形的面积为：a2+2×（a+a+b）•b＝a2+2zb+b2，
又∵大正方形的边长为（a+b），
∴大正方形的面积为：（a+b）2，
∴（a+b）2＝a2+2ab+b2．
故答案为：（a+b）2＝a2+ab+b（a+b）＝a2+2ab+b2，（a+b）2＝a2+2×（a+a+b）•b＝a2+2ab+b2．
（2）∵a﹣b＝2，ab＝3，
∴（a﹣b）2＝a2﹣2ab+b2，
∴4＝a2+b2﹣2×3，
∴a2+b2＝10，
∴（a+b）2＝a2+2ab+b2＝10+2×3＝16，
∵a，b均为正数，
∴a+b＝4．
28．（8分）（2023•余杭区开学）如图1是一个长为4a，宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成如图2的正方形．
（1）由图2可以直接写出（a+b）2，（a﹣b）2，ab之间的一个等量关系是 （a+b）2＝（a﹣b）2+4ab ；
（2）根据（1）中的结论，解决下列问题：3x+4y＝10，xy＝2，求3x﹣4y的值；
（3）两个正方形ABCD，AEFG如图3摆放，边长分别为x，y．若x2+y2＝58，BE＝4，求图中阴影部分面积和．
解：（1）∵大正方形的面积等于4个小长方形和小正方形面积之和，
∴（a+b）2＝4ab+（b﹣a）2．
∴（a+b）2＝（a﹣b）2+4ab．
故答案为：（a+b）2＝（a﹣b）2+4ab；
（2）由（1）得：（3x+4y）2＝（3x﹣4y）2+4×3x×4y．
∴（3x﹣4y）2＝（3x+4y）2﹣48xy
∴（3x﹣4y）2＝100﹣96＝4．
∴3x﹣4y＝±2；
（3）∵ABCD，AEFG为正方形，边长分别为x，y．BE＝4，
∴DG＝BE＝4，x﹣y＝4．
∴（x﹣y）2＝16．
∴x2﹣2xy+y2＝16．
∵x2+y2＝58，∴2xy＝42．
∴x2+2xy+y2＝42+58，
∴（x+y）2＝100．
∵x＞0，y＞0，
∴x+y＝10，
∴＝2（x+y）＝20