2024保定部分学校高一下学期13期中考试数学含解析

这是一份2024保定部分学校高一下学期13期中考试数学含解析，共25页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

第I卷（选择题）
一、单选题
1. 设（其中为虚数单位），若为纯虚数，则实数（ ）
A B. C. D.
2. 某种心脏手术，成功率为0.6，现采用随机模拟方法估计“3例心脏手术全部成功”的概率：先利用计算器或计算机产生0~9之间取整数值的随机数，由于成功率是0.6，故我们用0，1，2，3表示手术不成功，4，5，6，7，8，9表示手术成功；再以每3个随机数为一组，作为3例手术的结果.经随机模拟产生10组随机数：812，832，569，684，271，989，730，537，925，907.由此估计3例心脏手术全部成功的概率为（ ）
A. 0.2B. 0.3C. 0.4D. 0.5
3. 已知向量，的夹角为，若，则向量在向量上的投影向量为（ ）
A. B. C. D.
4. 下列命题中，正确的是（ ）
A. 直线、与平面所成的角相等，则
B. 、、三个平面，若，，则
C. 、、为空间中的三条直线，若，，则
D. 、为两条直线，、为两个平面，若，，，则
5. 已知直线：，则下列结论正确的是（ ）
A. 直线的倾斜角是
B. 若直线，则
C. 点到直线的距离是1
D. 过与直线平行的直线方程是
6. 如图，在中，，点在边上，且，则等于（ ）
A. B. C. D.
7. 如图，正方体的棱长为，为的中点，在侧面上，若，则面积的最小值为（ ）
A. B. C. D.
8. 已知圆与轴正半轴的交点为，从直线上任一动点向圆作切线，切点分别为，，过点作直线的垂线，垂足为，则的最小值为（ ）
A. B. C. 1D.
二、多选题
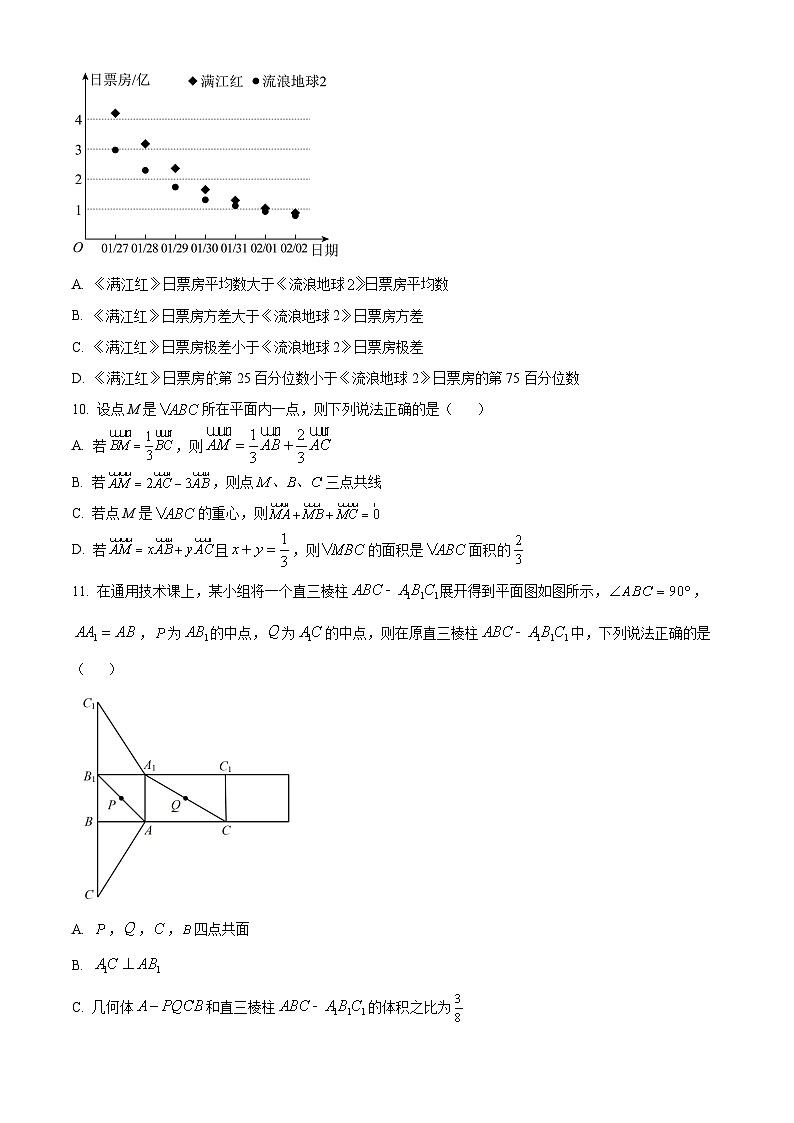
9. 今年春节档两部电影票房突破20亿大关，《满江红》不负众望，凭借喜剧元素和家国情怀，以25.96亿票房成为档期内票房冠军，另一部科幻续作《流浪地球2》则成为最高口碑电影．下图是这两部电影连续7天的日票房情况，则（ ）

A. 《满江红》日票房平均数大于《流浪地球日票房平均数
B. 《满江红》日票房方差大于《流浪地球2》日票房方差
C. 《满江红》日票房极差小于《流浪地球2》日票房极差
D. 《满江红》日票房第25百分位数小于《流浪地球2》日票房的第75百分位数
10. 设点M是所在平面内一点，则下列说法正确的是（ ）
A. 若，则
B. 若，则点三点共线
C. 若点M是的重心，则
D. 若且，则的面积是面积的
11. 在通用技术课上，某小组将一个直三棱柱展开得到平面图如图所示，，，为的中点，为的中点，则在原直三棱柱中，下列说法正确的是（ ）
A. ，，，四点共面
B.
C. 几何体和直三棱柱的体积之比为
D. 当时，与平面所成角为
第II卷（非选择题）
三、填空题
12. 已知两点，，过点的直线与线段有公共点，则直线的斜率的取值范围是___________.
13. 甲、乙两个篮球队进行比赛，获胜队将代表所在区参加市级比赛，他们约定，先赢四场比赛的队伍获胜．假设每场甲、乙两队获胜的概率均为，每场比赛不存在平局且比赛结果相互独立，若在前三场比赛中，甲队赢了两场，乙队赢了一场，则最终甲队获胜的概率为______．
14. 已知四面体中，，其余各棱长均为6，则四面体外接球的表面积为__________.
四、解答题
15. 从3个黑球，，和3个白球，，中任取3个：
（1）写出基本事件空间和基本事件总数n.
（2）求颜色都相同的概率；
（3）求恰有1个白球的概率.
16. 某市为了了解人们对“中国梦”的伟大构想的认知程度，针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（95分及以上为认知程度高），结果认知程度高的有20人，按年龄分成5组，其中第一组：，第二组：，第三组：，第四组：，第五组：，得到如图所示的频率分布直方图．

（1）根据频率分布直方图，估计这20人的年龄的中位数和众数；
（2）若第四组宣传使者的年龄的平均数与方差分别为37和，第五组宣传使者的年龄的平均数与方差分别为43和1，求这20人中35～45岁所有人的年龄的方差．
17. 在①；②；这两个条件中任选一个，补充在下面的问题中，并进行解答.
问题：在中，内角的对边分别为，且___________.
（1）求角；
（2）在中，，求周长的最大值.
注：如果选择多个条件分别解答，按第一个解答计分.
18. 矩形所在平面与等腰梯形所在平面互相垂直，，，直线与平面所成角为，.

（1）求平面与平面夹角的余弦值；
（2）线段上任意一点到平面的距离是否为定值?如果是，则求出定值，否则说明理由．
19. 已知圆，点P为直线上的动点．
（1）若从P到圆O切线长为，求P点的坐标以及两条切线所夹劣弧长；
（2）若点，直线与圆O的另一个交点分别为，求证：直线经过定点．河北省保定市部分学校2023-2024学年高一下学期1+3期中考试数学试题
第I卷（选择题）
一、单选题
1. 设（其中为虚数单位），若为纯虚数，则实数（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据复数乘法的运算法则，结合纯虚数的定义进行求解即可.
【详解】，
因为为纯虚数，
所以有，
故选：D
2. 某种心脏手术，成功率为0.6，现采用随机模拟方法估计“3例心脏手术全部成功”的概率：先利用计算器或计算机产生0~9之间取整数值的随机数，由于成功率是0.6，故我们用0，1，2，3表示手术不成功，4，5，6，7，8，9表示手术成功；再以每3个随机数为一组，作为3例手术的结果.经随机模拟产生10组随机数：812，832，569，684，271，989，730，537，925，907.由此估计3例心脏手术全部成功的概率为（ ）
A. 0.2B. 0.3C. 0.4D. 0.5
【答案】B
【解析】
【分析】利用古典概率的概率公式进行计算即可.
【详解】随机模拟产生10组随机数中，有3组随机数表示手术成功，
故3例心脏手术全部成功的概率为：.
故选：B
3. 已知向量，的夹角为，若，则向量在向量上的投影向量为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】由得，根据投影向量的定义求解.
【详解】由得，
即，
所以，
所以向量在向量上的投影向量为.
故选：A
4. 下列命题中，正确的是（ ）
A. 直线、与平面所成的角相等，则
B. 、、为三个平面，若，，则
C. 、、为空间中三条直线，若，，则
D. 、为两条直线，、为两个平面，若，，，则
【答案】D
【解析】
【分析】利用正四面体可判断A选项的正误；根据面面的位置关系可判断B选项的正误；根据空间中线线的位置关系可判断C选项的正误；根据线面垂直的性质可判断D选项的正误.
【详解】对于A选项，在正四面体中，、与平面所成角相等，但与相交，A选项错误；
对于B选项，若，，则与平行或相交，B选项错误；
对于C选项，若，，则与平行或相交，C选项错误；
对于D选项，由，得，由因为，所以，D选项正确.
故选：D.
【点睛】本题考查空间中线线、线面、面面位置关系的判断，考查推理能力，属于中等题.
5. 已知直线：，则下列结论正确的是（ ）
A. 直线倾斜角是
B. 若直线，则
C. 点到直线的距离是1
D. 过与直线平行的直线方程是
【答案】D
【解析】
【分析】求解直线的倾斜角判断A；利用直线的斜率乘积判断B；点到直线的距离判断C；求解直线方程判断D．
【详解】直线，直线的斜率为：，所以直线的倾斜角为：，所以A不正确；
直线的斜率为：，两条直线不垂直，所以B不正确；
点到直线的距离是：，所以C不正确；
过与直线平行的直线方程是，正确，所以D正确；
故选：D．
6. 如图，在中，，点在边上，且，则等于（ ）
A. B. C. D.
【答案】C
【解析】
【分析】在中，由余弦定理求得，在中，利用正弦定理求得BD，则可得CD.
【详解】在中，由余弦定理可得.
又，故为直角三角形，故.
因为，且为锐角，故.
由
利用正弦定理可得，代值可得，
故.
故选：C.
【点睛】本题考查利用正弦定理以及余弦定理解三角形，属于综合基础题.
7. 如图，正方体的棱长为，为的中点，在侧面上，若，则面积的最小值为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】以为原点建立空间直角坐标系，设，由可得，由此得到关系；从而利用表示的面积，利用二次函数最值求得面积的最值.
【详解】以为坐标原点可建立如下图所示空间直角坐标系
则，，，，，
设，则，

当时，
故选：
【点睛】本题考查立体几何中三角形面积最值的求解问题，关键是能够将所求三角形面积利用一个变量表示出来，得到二次函数的形式，利用二次函数的最值求得面积的最值.
8. 已知圆与轴正半轴的交点为，从直线上任一动点向圆作切线，切点分别为，，过点作直线的垂线，垂足为，则的最小值为（ ）
A. B. C. 1D.
【答案】B
【解析】
【分析】将直线转化为两个圆的公共弦方程，利用垂足确定的轨迹为一个圆,然后结合点到圆心的距离求最小值即可.
【详解】
易得，设，
因为是圆的两条切线，所以
所以在以为直径的圆上,
又因为,且的中点为，
所以以为直径的圆的方程为：.
所以为以为直径的圆和圆的的公共弦，
两个圆的方程相减得：
所以直线,
直线恒过定点，
过点作直线的垂线，垂足为,
则在以为直径的圆上，设圆的圆心为，半径为，
所以，
所以的最小值为:．
故选：B
二、多选题
9. 今年春节档两部电影票房突破20亿大关，《满江红》不负众望，凭借喜剧元素和家国情怀，以25.96亿票房成为档期内票房冠军，另一部科幻续作《流浪地球2》则成为最高口碑电影．下图是这两部电影连续7天的日票房情况，则（ ）

A. 《满江红》日票房平均数大于《流浪地球日票房平均数
B. 《满江红》日票房方差大于《流浪地球2》日票房方差
C. 《满江红》日票房极差小于《流浪地球2》日票房极差
D. 《满江红》日票房的第25百分位数小于《流浪地球2》日票房的第75百分位数
【答案】ABD
【解析】
【分析】根据图表信息逐一判断即可.
【详解】由图表可得《满江红》日票房都大于《流浪地球日票房，所以《满江红》日票房平均数大于《流浪地球2》日票房平均数，A正确;
由图可得《满江红》日票房单日票房数据波动更大，《满江红》日票房方差大于《流浪地球2》日票房方差，所以B正确.
《满江红》日票房极差大于《流浪地球日票房极差，故C错误；
因为，《满江红》日票房的第25百分位数是从小到大排序第个数，
因为，《流浪地球2》日票房的第75百分位数是从小到大排序第个数，
《满江红》日票房的第25百分位数小于《流浪地球2》日票房的第75百分位数，所以D正确.
故选：ABD.
10. 设点M是所在平面内一点，则下列说法正确的是（ ）
A. 若，则
B 若，则点三点共线
C. 若点M是的重心，则
D. 若且，则的面积是面积的
【答案】CD
【解析】
【分析】A选项，由平面向量基本定理，变形得到，A错误；假设点M、B、C三点共线，推导出，故B错误；C选项，画出图形，结合向量加法法则及重心的概念及性质得到答案；D选项，可以先得到的面积与面积底相同，高线之比为2:3，从而得到答案.
【详解】A选项，，A错误；
B选项，假设点M、B、C三点共线，则，即，
整理得：，
故当时，即，与条件中的不一致，
所以点M、B、C三点不共线，B错误；
如图，取BC中点H，连接AH，若点M是的重心，则点M在AH上，且MA=2MH，则，则，C正确；
D选项，由于，而，所以，其中，不妨设，则Q点在直线BC上，由于与同底，而高线之比等于与的比，即比值为2:3，所以的面积是面积的，D正确.
故选：CD
11. 在通用技术课上，某小组将一个直三棱柱展开得到平面图如图所示，，，为的中点，为的中点，则在原直三棱柱中，下列说法正确的是（ ）
A. ，，，四点共面
B.
C. 几何体和直三棱柱的体积之比为
D. 当时，与平面所成的角为
【答案】ABD
【解析】
【分析】根据线面位置关系可判断A，B选项，根据几何体的体积计算方法即可判断C选项，利用定义法可判断线面角，即可判断D选项
【详解】如图，将展开的平面图还原成立体图形，
对A选项，连接，为的中点，也为的中点，又为的中点，，，，，四点共面，故A选项正确；
对B选项，，棱柱为直三棱柱，易得平面，又平面，，又，四边形为正方形，，又，平面，又平面，，B选项正确；
对C选项，，分别为，的中点，，
几何体和直三棱柱的体积之比为，
故C选项错误；
对D选项，当时，又，且，，，，又由B选项的分析知平面，即为与平面所成的角，又，与平面所成的角为，故D选项正确．
故选：ABD．
第II卷（非选择题）
三、填空题
12. 已知两点，，过点的直线与线段有公共点，则直线的斜率的取值范围是___________.
【答案】
【解析】
【分析】根据两点间的斜率公式，利用数形结合即可求出直线斜率的取值范围．
【详解】解：点，，过点的直线与线段有公共点，
直线的斜率或，
的斜率为，的斜率为，
直线的斜率或，即，
故答案为：．
13. 甲、乙两个篮球队进行比赛，获胜队将代表所在区参加市级比赛，他们约定，先赢四场比赛的队伍获胜．假设每场甲、乙两队获胜的概率均为，每场比赛不存在平局且比赛结果相互独立，若在前三场比赛中，甲队赢了两场，乙队赢了一场，则最终甲队获胜的概率为______．
【答案】##
【解析】
【分析】考虑先赢四场比赛的队伍获胜，甲队已经赢了两场，故只需再先赢两场则获胜，分析得到甲在随后进行的场次可以有两场连胜，也可输一场赢两场（含两种情况），还可以输两场赢两场（含三种情况），分别计算概率，再利用互斥事件的概率加法公式即得.
【详解】由题意得甲、乙两队获胜的概率均为，且最多再进行四场比赛，最少再进行两场比赛.
则①再进行两场比赛甲队获胜的概率为；
②再进行三场比赛甲队获胜的概率为；
③再进行四场比赛甲队获胜的概率为，
由互斥事件的概率加法公式，可得最终甲队获胜的概率为．
故答案为.
14. 已知四面体中，，其余各棱长均为6，则四面体外接球的表面积为__________.
【答案】
【解析】
【分析】作图，由余弦定理计算，再得，利用正弦定理可求得底面外接圆的半径，再计算得的值，列方程，代入求解出，从而可求解出，代入表面积公式计算.
【详解】如图，设外接球的球心为，半径为，底面的外心为，底面外接圆的半径为，因为，其余各棱长均为，所以可得，所以，由正弦定理得，即，所以，因为，可得，求解得，所以，所以外接球的表面积为.
故答案为：
【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图.
四、解答题
15. 从3个黑球，，和3个白球，，中任取3个：
（1）写出基本事件空间和基本事件总数n.
（2）求颜色都相同的概率；
（3）求恰有1个白球的概率.
【答案】（1）见解析，28（2）（3）
【解析】
【分析】（1）根据列举法按找一定的次序不重不漏的列出基本事件即可.
（2）由（1）即可找出同色的基本事件，再利用古典概型的概率计算公式即可求解.
【详解】（1）

，即
（2）“颜色都相同”，则，，
则
（3）同理，“恰有1个白球”，
则
，共个基本事件，
求得.
【点睛】本题考查了基本事件的列举以及古典概型的概率计算公式，属于基础题.
16. 某市为了了解人们对“中国梦”的伟大构想的认知程度，针对本市不同年龄和不同职业的人举办了一次“一带一路”知识竞赛，满分100分（95分及以上为认知程度高），结果认知程度高的有20人，按年龄分成5组，其中第一组：，第二组：，第三组：，第四组：，第五组：，得到如图所示的频率分布直方图．

（1）根据频率分布直方图，估计这20人的年龄的中位数和众数；
（2）若第四组宣传使者的年龄的平均数与方差分别为37和，第五组宣传使者的年龄的平均数与方差分别为43和1，求这20人中35～45岁所有人的年龄的方差．
【答案】（1）中位数为，众数为
（2）10
【解析】
【分析】（1）根据频率分布直方图求中位数及众数即可；
（2）先根据分层抽样求出第四组和第五组抽取的人数，再求出第四组和第五组所有宣传使者的年龄平均数和方差，进而可得出答案.
【小问1详解】
由于，
所以这20人的年龄的中位数为：，
众数为：；
【小问2详解】
由频率分布直方图得各组人数之比为，
故各组中采用分层随机抽样的方法抽取20人，第四组和第五组分别抽取4人和2人，
设第四组、第五组的宣传使者的年龄的平均数分别为，方差分别为，
则，
设第四组和第五组所有宣传使者的年龄平均数为，方差为，
则，
因此，第四组和第五组所有宣传使者的年龄方差为10，
据此，可估计这人中年龄在35～45岁的所有人的年龄方差约为10．
17. 在①；②；这两个条件中任选一个，补充在下面的问题中，并进行解答.
问题：在中，内角的对边分别为，且___________.
（1）求角；
（2）在中，，求周长的最大值.
注：如果选择多个条件分别解答，按第一个解答计分.
【答案】（1）
（2）
【解析】
【分析】（1）选择①：由正弦定理化边为角即可求出；选择②：利用面积公式和数量积关系化简可得出；
（2）利用余弦定理结合基本不等式即可求出.
【小问1详解】
选择①：条件即，
由正弦定理可知，，
在中，，所以，
所以，且，即，所以；
选择②：条件即，
即，.
在中，，所以，则，
所以，所以.
【小问2详解】
由（1）知，
由余弦定理知：
所以得
所以，当且仅当时，等号成立
所以求周长的最大值为.
18. 矩形所在平面与等腰梯形所在平面互相垂直，，，直线与平面所成角为，.

（1）求平面与平面夹角的余弦值；
（2）线段上任意一点到平面的距离是否为定值?如果是，则求出定值，否则说明理由．
【答案】（1）
（2）是定值，
【解析】
【分析】（1）建立空间直角坐标系，结合题意可求得相关点坐标，进而求得平面与平面的法向量，根据空间角的向量求法可得答案；
（2）根据线面平行的判定定理可证明平面，从而可判断段上任意一点到平面的距离为定值，利用空间距离的向量求法可求得定值.
【小问1详解】
过点F作,垂足为G，
因为平面平面，平面平面，平面,
故平面，则为直线与平面所成角，即，
过点C作平面的垂线作为z轴，以为轴，建立空间直角坐标系，

因为，
在等腰梯形中，，
则，
，
设平面的法向量为，
则，令，则，
故，
平面一个法向量可取为，
故，
故平面与平面夹角的余弦值为.
【小问2详解】
设交于点H，连接，
因为,且，故四边形为平行四边形，
则，平面，平面，
故平面，
所以线段上任意一点到平面的距离是否为定值，
又，
故A点到平面的距离为，
即定值为.
19. 已知圆，点P为直线上的动点．
（1）若从P到圆O的切线长为，求P点的坐标以及两条切线所夹劣弧长；
（2）若点，直线与圆O的另一个交点分别为，求证：直线经过定点．
【答案】（1），
（2）证明见解析
【解析】
【分析】（1）设出P点坐标，根据切线长与几何关系即可求出P点的坐标以及两条切线所夹劣弧长.
（2）根据题意求出坐标，证明直线与点三点共线即可.
【小问1详解】
根据题意，设，
设两切点为，则，，
由题意可知，即，
解得，所以点P坐标为．
在中，易得，
所以，
所以两条切线所夹劣弧长为.
【小问2详解】
设，
依题意，直线经过点，
可以设，
和圆联立，得到，
代入消元得到，，
因为直线经过点，所以是方程的两个根，
所以有，
代入直线方程得，．
同理，设，联立方程有，
代入消元得到，
因为直线经过点，所以是方程的两个根，
，
代入得到．
若，则，此时，
显然三点在直线上，即直线经过定点，
若则，
所以有，
所以，所以三点共线，
即直线经过定点．
综上所述，直线经过定点．