2024年甘肃省武威市凉州区下双中学联片教研九年级数学第三次模拟试题（原卷版+解析版）

这是一份2024年甘肃省武威市凉州区下双中学联片教研九年级数学第三次模拟试题（原卷版+解析版），文件包含2024年甘肃省武威市凉州区下双中学联片教研九年级数学第三次模拟试题原卷版docx、2024年甘肃省武威市凉州区下双中学联片教研九年级数学第三次模拟试题解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
一、选择题(共30分)
1. 3的倒数是（ ）
A. B. C. D.
2. 如果与是同类项，则的值为（ ）
A 4B. C. 8D. 12
3. 若关于x，y的方程组的解满足，则m的最小整数解为（ ）
A. ﹣3B. ﹣2C. ﹣1D. 0
4. 如图，中，，沿将此三角形对折，又沿再一次对折，点C落在上的处，此时，则原三角形的的度数为（ ）

A. B. C. D.
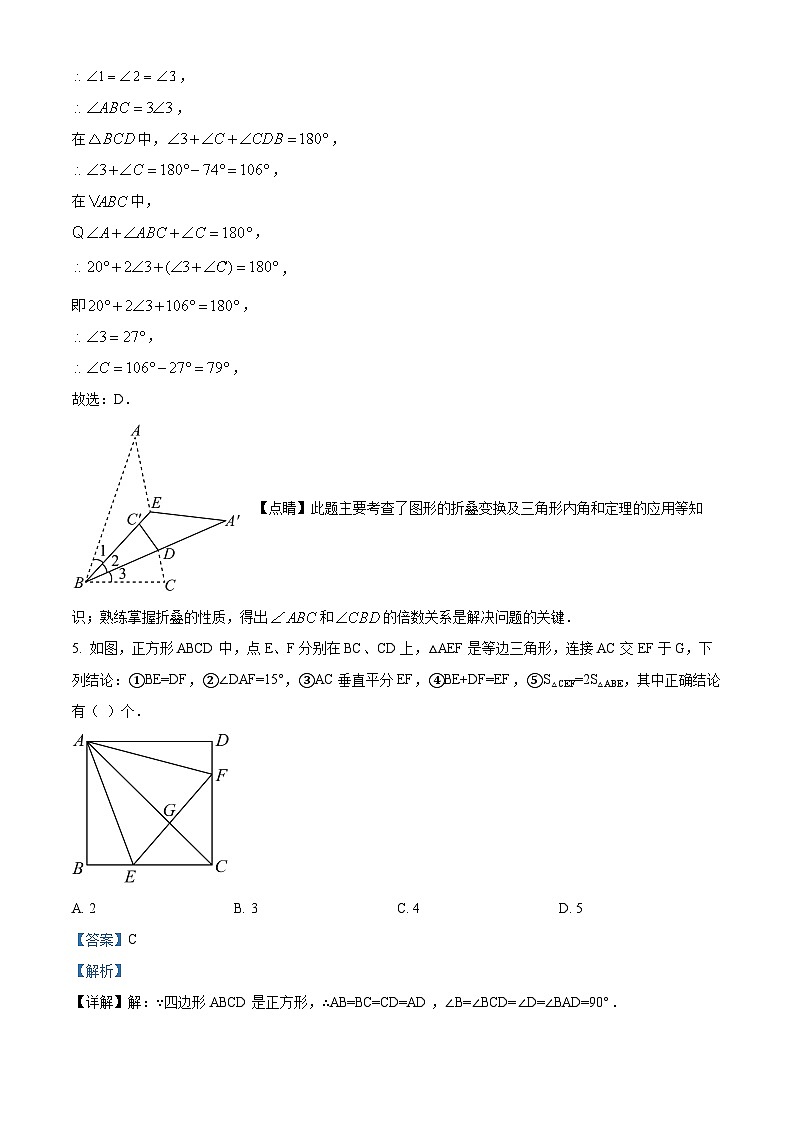
5. 如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△CEF=2S△ABE，其中正确结论有（ ）个．
A. 2B. 3C. 4D. 5
6. 如图，边长为2的正方形的中心与坐标原点重合，轴，将正方形绕原点顺时针旋2023次，每次旋转，则顶点的坐标是（ ）

A. B. C. D.
7. 如图，在⊙O中，，. 则的度数为（ ）
A. B. C. D.
8. 如图，在平面直角坐标系中，菱形ABCD的顶点D在第二象限，其余顶点都在第一象限，AB∥X轴，AO⊥AD，AO=AD．过点A作AE⊥CD，垂足为E，DE=4CE．反比例函数的图象经过点E，与边AB交于点F，连接OE，OF，EF．若，则k的值为（ ）
A. B. C. 7D.
9. 如图，已知，，，，则的长为（ ）

A. B. C. D.
10. 如图，⊙O是△ABC的外接圆，直径BD长为4，sin∠BAC＝，则BC的长为（ ）
A. B. 3C. D.
二、填空题(共24分)
11. 已知一个边形的内角和等于1980°，则__________．
12. 因式分解：=______．
13. 已知样本、、、的平均数是5，方差是3，则样本、、、的方差是_______．
14. 如图，在中，，，将绕点按逆时针方向旋转得到，满足，过点作，垂足为，连接，若，则长为______．
15. 如图，正方形ABCD中，扇形BAC与扇形CBD的弧交于点E，AB＝6cm．则图中阴影部分面积为___cm2．
16. 在平面直角坐标系中，，，C在直线上运动，存在一点P，满足，则的最小值为______．
17. 如图，已知路灯离地面的高度AB为4.8m，身高为1.6m的小明站在D处的影长为2m，那么此时小明离电杆AB的距离BD为_____m．
18. 如图，将圆形纸片折叠使弧经过圆心O，过点O作半径于点E，点P为圆上一点，则的度数为______．
三、计算题(共8分)
19. （1）解不等式，并将解集数轴上表示出来：
（2）计算：．
四、作图题(共4分)
20. 如图，是由小正方形组成的9×6网格，每个小正方形的顶点叫做格点，的三个顶点都是格点，仅用无刻度的直尺在网格中画图，画图过程用虚线，画图结果用实线表示．
（1）如图1，在上画一点E，使=；过点E作，垂足F；
（2）如图2， D是网格中的格点，在线段上找一点，使得平分；在上找点，连接，使．
五、解答题(共54分)
21. 如图，点B，F，C，E在一条直线上，AB=DE，∠B=∠E，BF=CE．求证：AC=DF．
22. 如图所示，已知平行四边形ABCD的对角线交于O，过O作直线交AB、CD的反向延长线于E、F，求证：OE＝OF．
23. 为了加强中小学学生的劳动教育，2024年计划将该区的土地作为社会实践基地，该基地准备种植甲乙两种蔬菜．经调查发现：甲种蔬菜种植成本y（单位：元）与其种植面积x（单位：）的函数关系，其中；乙种蔬菜的种植成本为50元．
（1）设2024年甲乙两种蔬菜总种植成本为w元，如何分配两种蔬菜的种植面积，使w最小？
（2）学校计划今后每年在这土地上，均按（1）中方案种植蔬菜，因技术改进，预计种植成本逐年下降．若甲种蔬菜种植成本平均每年下降，乙种蔬菜种植成本平均每年下降，当a为何值时，2026年总种植成本为28920元？
24. 如图，点E是正方形内一点，将绕点A顺时针旋转至，点E的对应点为点F．
（1）若，，求的度数．
（2）连接，若，求线段的长．
25. 如图，在中，是直径，弦，垂足为点，连结．

（1）求证：．
（2）若，求的长度．
26. 甲、乙两个盒子中装有质地、大小相同的小球，甲盒中有2个白球、1个黄球和1个蓝球；乙盒中有1个白球、2个黄球和若干个蓝球．从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球为蓝球的概率的2倍．
（1）求乙盒中蓝球的个数．
（2）从甲、乙两盒中分别任意摸取一球，利用列表或画树状图法求这两球均为蓝球的概率．
27. 如图，在平面直角坐标系中，点，．抛物线交轴于，两点，交轴于点．
（1）求抛物线的解析式；
（2）当时，求的最小值；
（3）连接，若二次函数的图象向上平移个单位时，与线段有一个公共点，结合函数图象，直接写出的取值范围．