北师大版七年级数学上册《认识一元一次方程》第2课时课件PPT

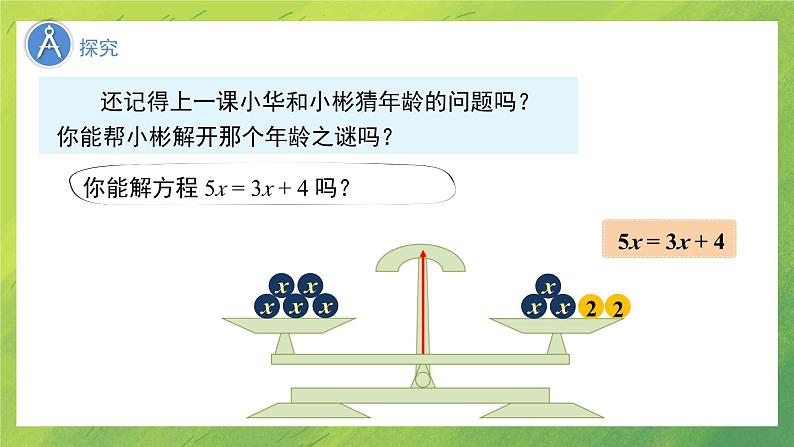
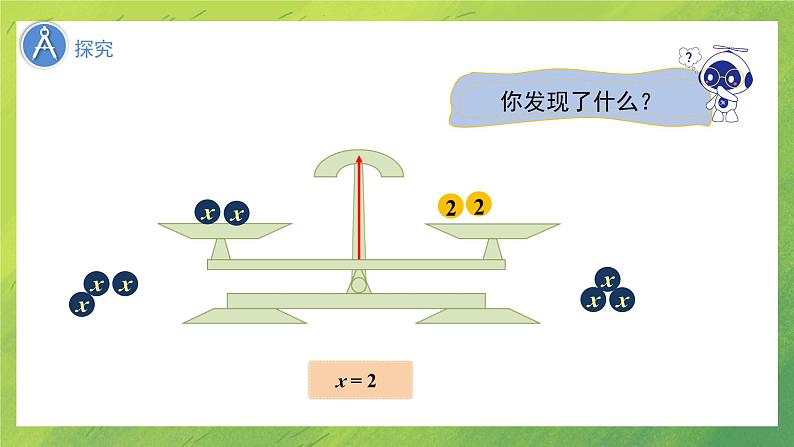
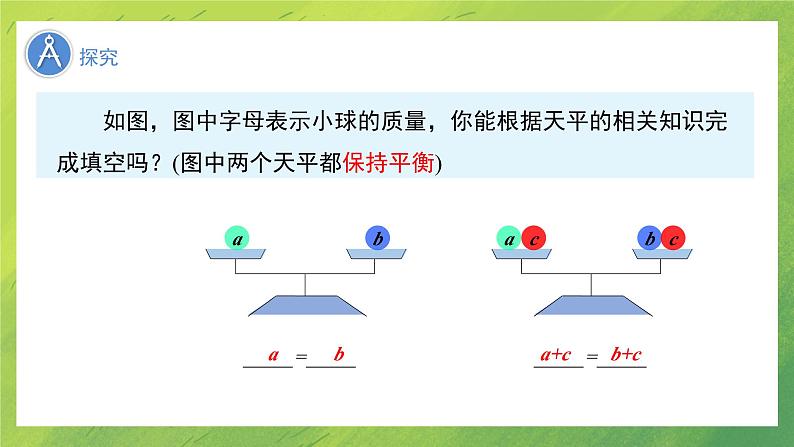
LOGO北师大版 数学 七年级 上册5.1 认识一元一次方程 （第2课时）什么是方程？等式和方程的关系是什么？等式等式方程 在一个方程中，只含有一个未知数，而且方程中的代数式都是整式，未知数的指数都是1，这样的方程叫做一元一次方程. 一元一次方程方程的解：使方程左、右两边的值相等的未知数的值，叫做方程的解.1. 能用文字和数学式子表达等式的两个性质.2. 借助直观对象理解等式的基本性质.3. 能用等式的性质解简单的一元一次方程. 还记得上一课小华和小彬猜年龄的问题吗？你能帮小彬解开那个年龄之谜吗？ 如图，图中字母表示小球的质量，你能根据天平的相关知识完成填空吗？(图中两个天平都保持平衡)cc_____=_____ab_____=_____a+cb+c从左到右，等式发生了怎样的变化？ _____=__________=_____aba+cb+c 从右到左呢？减去? ? 由等式1+2=3，进行判断： 1+2 ＝ 3 1.上述两个问题反映出等式具有什么性质？ 1+2 ＝ 3 等式的两边都加上(或减去)同一个数所得的结果仍是等式． 由等式2x+3x=5x，进行判断： ? 2x+3x ＝ 5x ? 2x+3x ＝ 5x 上述两个问题反映出等式具有什么性质？ 等式的两边都加上(或减去) 同一个式子，所得的结果仍是等式． 等式两边同时加(或减)同一个代数式，所得结果仍是等式.用字母可以表示为：如果a=b，那么a±c=b±c. 等式的性质1：在下面的括号内填上适当的数或者式子：（1）因为： 所以：（2）因为： 所以：（3）因为： 所以：练一练_____=_____ab_____=_____3a3b 如图，图中字母表示小球的质量，你能根据天平的相关知识完成填空吗？(图中两个天平都保持平衡)等式的两边都 乘以 同一个数，等式仍然成立.除以从左到右，等式发生了怎样的变化？ 从右到左呢？? ? 由等式3m+5m=8m ，进行判断： 上述两个问题反映出等式具有什么性质？ 3m+5m ＝ 8m 3m+5m ＝ 8m 等式两边同时乘同一个数(或除以同一个不为0的数)，所得结果仍是等式.用字母可以表示为：如果a=b，那么ac=bc或 (c≠0). 等式的性质2：性质1：等式两边同时加上 (或减去) 同一个代数式，所得 结果仍是等式.性质2：等式两边同时乘同一个数（或除以同一个不为0的数） 所得结果仍是等式.注意：（1）等式两边都要参加运算，且是同一种运算；（2）等式两边加或减，乘或除以的数一定是同一个数或同 一个式子；（3）等式两边不能都除以０，即０不能作除数或分母．等式的基本性质 (2) 怎样从等式 3+x=1 得到等式 x =－2?(3) 怎样从等式 4x=12 得到等式 x =3?依据等式的性质1两边同时减3.例1 (1) 怎样从等式 x－5= y－5 得到等式 x = y ?依据等式的性质1两边同时加5.识别等式变形的依据(2) 从 a+2=b+2 能不能得到 a=b，为什么?(3) 从－3a=－3b 能不能得到 a=b，为什么?(4) 从 3ac=4a 能不能得到 3c=4，为什么?能，根据等式的性质2，两边同时除以9.能，根据等式的性质1，两边同时加上2.能，根据等式的性质2，两边同时除以-3.不能，a可能为0.指出等式变形的依据例2 已知mx=my，下列结论错误的是 （ ） A. x=y B. a+mx=a+my C. mx－y=my－y D. amx=amyA判断等式变形的对错易错提醒：此类判断等式变形是否正确的题型中，尤其注意利用等式的性质2等式两边同除某个字母，只有这个字母确定不为0时，等式才成立.判断对错，对的说明根据等式的哪一条性质；错的说出为什么.(1)如果x=y,那么                     （      ）   (2)如果x=y,那么x+5-a=y +5-a （      ）(3)如果x=y,那么                     （      ）(4)如果x=y,那么-5x=-5y       （      ） (5)如果x=y,那么                    （      ）  ×√××√左边加右边减，等式不成立当a=5时，无意义两边乘的数不相等等式性质1等式的性质1和性质2利用等式的性质解方程 利用等式的性质解下列方程： 解:得 方程两边同时减去2，x + 2 = 5 于是 = x3.小结：解一元一次方程要“化归”为“ x=a ”的形式. (2) 3=x -5. (1) x + 2 = 5; 于是 8=x3+5= x－5+5 习惯上，我们写x=8. 例1 于是 x = 3解：(1)方程两边同时减2，得 x + 2 - 2 = 5 – 2例2 解下列方程(1) x+2=5； (2) 3=x-5.(2)方程两边同时加 5，得3 + 5 = x - 5 + 5于是 8 = x习惯上，我们写成 x = 8.利用等式的基本性质可以解一元一次方程.思考：为使（1）中未知项的系数化为1，将要用到等式的什么性质 ？例3解下列方程： 化简，得 x=－5.-3x÷(－3)= 15 ÷(－3) (1) －3x = 15 (2)解：方程两边同时加上2,得 化简,得  x=－36是原方程的解吗?思考：对比(1)，(2)有什么新特点？(2)利用等式的基本性质可以解一元一次方程.  一般地，从方程解出未知数的值以后，可以代入原方程检验，看这个值能否使方程的两边相等. 例如，将 x = －36 代入方程 的左边，方程的左右两边相等，所以 x = －36 是原方程的解.怎么验证方程的解？ 利用等式的性质时要注意什么？(1)等式两边都要参加运算，且是同一种运算；(2)等式两边加或减，乘或除以的数一定是同一个数或同一个式子；(3)等式两边不能都除以0，即0不能做除数或分母.(1)利用等式的基本性质1，把方程中含有未知数的项移到方程的左边，常数项移到方程的右边，即把方程变形为ax=b(a≠0)的形式；(2)利用等式的基本性质2，在方程两边同时除以未知数的系数，使未知数的系数化为1．利用等式的基本性质解一元一次方程的一般步骤： (1) x+6 = 17 ; (2) -6x = 18 ; (3) 2x-1 = -3 ; 解：(1)两边同时减去6，得x=11. (2)两边同时除以-6，得x=-3. (3)两边同时加上1，得2x=-2. 两边同时除以2，得x=-1. 两边同时乘以-3，得x=9. 利用等式的性质解下列方程:AB加3122减y1除以x2解：（1）x=6+5,x=11,把x=11代入方程x-5=6，得11-5=6，等于右边，所以x=11是方程的解.（2）x=45÷0.3,x=150,把x=150代入方程 ，得 0.3×150=45，等于右边，所以x=150是方程的解.利用等式的性质解下列方程并检验：把 代入方程 5x+4=0，得 ，等于右边，所以 是方程的解. （3）5x=-4（4）把x=-4代入方程 ，得 等于右边，所以x=-4是方程的解.认识一元一次方程等式的基本性质1： 等式两边同时加(或减)同一个代数式，所得结果仍是等式.利用等式的基本性质可以解一元一次方程.等式的基本性质2： 等式两边同时乘同一个数(或除以同一个不为0的数)，所得结果仍是等式.