2024年中考数学复习讲义 第20讲 图形的相似与位似(含答案)

这是一份2024年中考数学复习讲义 第20讲 图形的相似与位似(含答案)，共73页。学案主要包含了考情分析，知识建构等内容，欢迎下载使用。
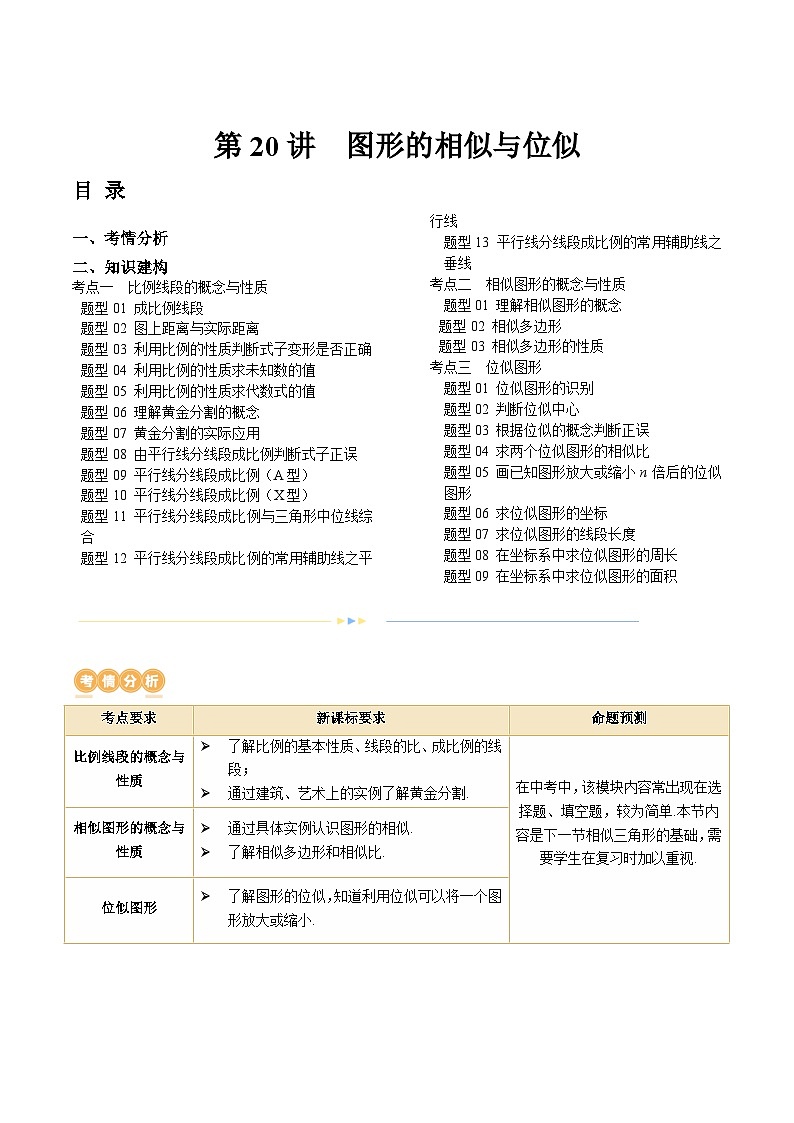
TOC \ "1-3" \n \h \z \u 一、考情分析
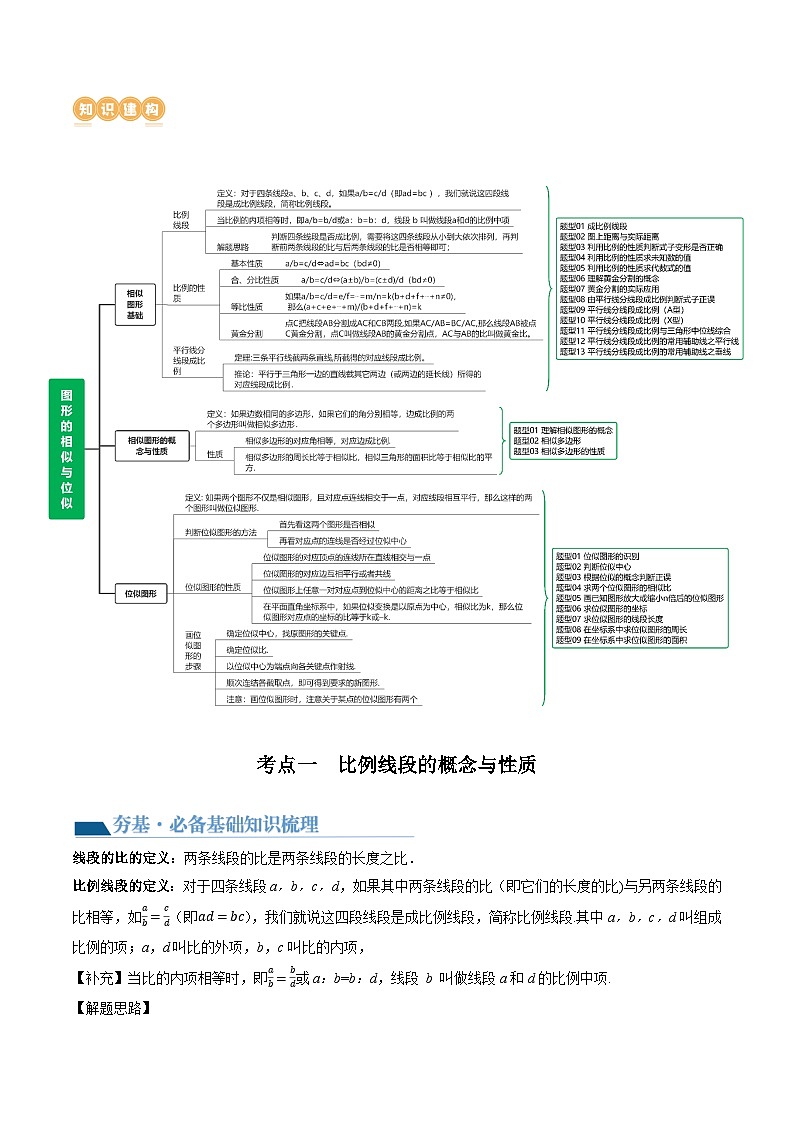
二、知识建构
考点一 比例线段的概念与性质
题型01 成比例线段
题型02 图上距离与实际距离
题型03 利用比例的性质判断式子变形是否正确
题型04 利用比例的性质求未知数的值
题型05 利用比例的性质求代数式的值
题型06 理解黄金分割的概念
题型07 黄金分割的实际应用
题型08 由平行线分线段成比例判断式子正误
题型09 平行线分线段成比例（A型）
题型10 平行线分线段成比例（X型）
题型11 平行线分线段成比例与三角形中位线综合
题型12 平行线分线段成比例的常用辅助线之平行线
题型13 平行线分线段成比例的常用辅助线之垂线
考点二 相似图形的概念与性质
题型01 理解相似图形的概念
题型02 相似多边形
题型03 相似多边形的性质
考点三 位似图形
题型01 位似图形的识别
题型02 判断位似中心
题型03 根据位似的概念判断正误
题型04 求两个位似图形的相似比
题型05 画已知图形放大或缩小n倍后的位似图形
题型06 求位似图形的坐标
题型07 求位似图形的线段长度
题型08 在坐标系中求位似图形的周长
题型09 在坐标系中求位似图形的面积
考点一 比例线段的概念与性质
线段的比的定义：两条线段的比是两条线段的长度之比．
比例线段的定义：对于四条线段a，b，c，d，如果其中两条线段的比（即它们的长度的比)与另两条线段的比相等，如ab=cd（即ad=bc），我们就说这四段线段是成比例线段，简称比例线段.其中a，b，c，d叫组成比例的项；a，d叫比的外项，b，c叫比的内项，
【补充】当比的内项相等时，即ab=bd或a：b=b：d，线段 b 叫做线段a和d的比例中项.
【解题思路】
1）判断四条线段是否成比例，需要将这四条线段从小到大依次排列，再判断前两条线段的比与后两条线段的比是否相等即可；
2）成比例的线段是有顺序的，比如：a，b，c，d是成比例的线段，则成比例线段只能写成ab=cd（即：第一条第二条=第三条第四条），而不能写成ab=dc.
比例的性质：
1）基本性质：ab=cd⇔ad=bc ab=bc⇔b2=ac
2）变形：ab=cd⇔&ac=bd，(交换内项)&db=ca，(交换外项)&dc=ba．(同时交换内外项) 核心内容：ad=bc
3）合、分比性质：ab=cd⇔a±bb=c±dd
【补充】实际上，比例的合比性质可扩展为：比例式中等号左右两个比的前项，后项之间发生同样和差变化比例仍成立．如：ab=cd⇒&b-aa=d-cc&a-ba+b=c-dc+d
4）等比性质：如果ab=cd=ef=⋯=mn=k， 那么a+c+e+⋯+mb+d+f+⋯+n=k(b+d+f+⋯+n≠0).
【补充】根据等比的性质可推出，如果ab=cd，则ab=cd=a+cb+d(b+d≠0).
5）黄金分割：点C把线段AB分割成AC和CB两段,如果ACAB=BCAC,那么线段AB被点C黄金分割，点C叫做线段AB的黄金分割点，AC与AB的比叫做黄金比.
【注意】1）AC=5-12AB≈0.648AB (5-12叫做黄金分割值). 简记为：
2）一条线段的黄金分割点有两个.
【扩展】作一条线段的黄金分割点：
如图，已知线段AB，按照如下方法作图：
①经过点B作BD⊥AB，使BD=12AB.
②连接AD，在DA上截取DE=DB.
③在AB上截取AC=AE.则点C为线段AB的黄金分割点.
6）平行线分线段成比例定理
平行线分线段成比例定理:三条平行线截两条直线,所截得的对应线段成比例.
①已知l3∥l4∥l5, 可得ABBC=DEEF或ABAC=DEDF或BCAB=EFDE或BCAC=EFDF或ABDE=BCEF等
①把平行线分线段成比例的定理运用到三角形中，会出现下面的两种情况：
推论：平行于三角形一边的直线截其它两边（或两边的延长线）所得的对应线段成比例．
1. 求线段之比时，要先统一线段的长度单位，最后的结果与所选取的单位无关系．
2. 通常四条线段a，b，c，d的单位应该一致，但有时为了计算方便，a和b统一为一个单位，c和d统一为另外一个单位也可以.
题型01 成比例线段
【例1】（2023·福建泉州·校联考模拟预测）下列长度的各组线段中，能构成比例线段的是（ ）
A．2，5，6，8B．3，6，9，2C．1，2，3，4D．3，6，7，9
【答案】B
【分析】分别计算各组数中最大与最小数的积和另外两数的积，然后根据比例线段的定义进行判断．
【详解】解：A.∵2×8≠5×6，
∴2，5，6，8不能构成比例线段，不符合题意；
B.∵2×9=3×6，
∴3，6，9，2能构成比例线段，符合题意；
C.∵1×4≠3×2，
∴1，2，3，4不能构成比例线段，不符合题意；
D.∵3×9≠6×7，
∴3，6，7，9不能构成比例线段，不符合题意；
故选B．
【点拨】本题考查了比例线段：判定四条线段是否成比例，只要把四条线段按大小顺序排列好，判断前两条线段之比与后两条线段之比是否相等即可，求线段之比时，要先统一线段的长度单位，最后的结果与所选取的单位无关系．
【变式1-1】（2023·上海长宁·统考一模）已知线段a，b，c，d是成比例线段，如果a=1，b=2，c=3，那么d的值是（ ）
A．8B．6C．4D．1
【答案】B
【分析】利用成比例线段的定义得到a:b=c:d，然后根据比例的性质求d的值．
【详解】解：根据题意得：a:b=c:d，
即1:2=3:d，
解得d=6．
故选：B．
【点拨】本题考查了比例线段：对于四条线段a，b，c，d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如a:b=c:d（即ad=bc），我们就说这四条线段是成比例线段．
【变式1-2】（2023·上海杨浦·统考一模）已知线段a=3厘米，c=12厘米，如果线段b是线段a和c的比例中项，那么b= 厘米．
【答案】6
【分析】本题考查了比例线段，根据比例中项的定义得到a:b=b:c，然后利用比例性质计算即可，解题的关键是理解四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，a:b=c:d，我们就说这四条线段是成比例线段，简称比例线段，当a:b=b:c时，线段b是线段a和c的比例中项．
【详解】∵线段b是线段a和c的比例中项，
∴a:b=b:c， 即b2=ac=3×12，
∴b=6cm，
故答案为：6 ．
题型02 图上距离与实际距离
【例2】（2023·江苏常州·常州市第二十四中学校考模拟预测）在比例尺是1:8000的地图上，延陵西路的长度约为25 cm，该路段的实际长度约为（ ）
A．3200 mB．3000mC．2400mD．2000m
【答案】D
【分析】首先设它的实际长度是xcm然后根据比例尺的定义，即可得方程1:8000=25:x，解此方程即可求得答案，注意统一单位．
【详解】解：设它的实际长度为xcm，
根据题意得：1:8000=25:x
解得：x=200000，
∵200000cm=2000m
∴该路段实际长度约为2000m
故选：D．
【点拨】此题考查了比例线段．此题难度不大，解题的关键是理解题意，根据比例尺的定义列方程，注意统一单位．
【变式2-1】（2023·上海嘉定·校考一模）甲、乙两地的实际距离为250km，如果画在比例尺为1:5 000 000的地图上，那么甲、乙两地的图上距离是 cm．
【答案】5
【分析】根据比例尺＝图上距离÷实际距离进行求解即可．
【详解】解：由题意得甲、乙两地的图上距离是250×1000×100×15000000=5cm，
故答案为：5．
【点拨】本题主要考查了比例尺，熟知比例尺的定义是解题的关键．
题型03 利用比例的性质判断式子变形是否正确
【例3】（2023·安徽合肥·校考一模）已知2x=3y（x≠0，y≠0），则下列比例式成立的是（ ）
A．x3=y2B．x2=3yC．x2=y3D．xy=23
【答案】A
【分析】根据若ab=cd(b≠0，d≠0)，则ad=bc，进行逐一判断即可求解．
【详解】解：A.可化为2x=3y，故此项符合题意；
B. 可化为xy=6，故此项不符合题意；
C. 可化为3x=2y，故此项不符合题意；
D. 可化为3x=2y，故此项不符合题意．
故选：A．
【点拨】本题考查了比例是性质，掌握性质是解题的关键．
【变式3-1】（2023·上海宝山·一模）已知线段a，b，如果a:b=2:3，那么下列各式中一定正确的是（ ）
A．2a=3bB．a+b=5C．a+ba=52D．a+3b+2=1
【答案】C
【分析】根据比例的性质进行判断即可．
【详解】解：A.由a:b=2:3，得3a=2b，故本选项错误，不符合题意；
B.当a=4，b=6时，a:b=2:3，但是a+b=10，故本选项错误，不符合题意；
C.由a:b=2:3，得a+ba=52，故本选项正确，符合题意；
D.当a=4，b=6时，a:b=2:3，但是a+3b+2=78，故本选项错误，不符合题意．
故选：C．
【点拨】本题考查了比例的性质及式子的变形，用到的知识点：在比例里，两外项的积等于两内项的积，比较简单．
题型04 利用比例的性质求未知数的值
【例4】（2023·湖南郴州·模拟预测）若5-x:x=2:3，则x= ．
【答案】3
【分析】根据比例的性质得到方程35-x=2x，再解方程即可求解．
【详解】解：∵5-x:x=2:3，
∴35-x=2x，
15-3x=2x，
解得x=3．
故答案为：3．
【点拨】本题考查比例性质，熟练掌握内项之积等于外项之积是解题关键．
【变式4-1】（2023·四川成都·统考二模）若ab=34，且a+b=7，则a的值为 ．
【答案】
【分析】根据比例的性质得到3b=4a，结合a+b=7求得a的值即可．
【详解】解：由a：b=3：4知3b=4a，
所以b=43a.
所以由a+b=7得到：a+43a=7，
解得：a=3，
故答案为：3．
【点拨】考查了比例的性质，内项之积等于外项之积．若ab=cd，则ad=bc．
题型05 利用比例的性质求代数式的值
【例5】（2023·浙江·模拟预测）用“▲”，“●”，“◆”分别表示三种物体的重量，若▲●=●-◆▲=◆●+▲，则▲，●，◆这三种物体的重量比为（ ）
A．2:3:4B．2:4:3C．3:4:5D．3:5:4
【答案】B
【分析】可设▲●=●-◆▲=◆●+▲ =k，利用等比性质可得k的值，设▲为x，●为y，◆为z，得到3个等式，联立可得用x表示y、z，相比即可．
【详解】解：设▲●=●-◆▲=◆●+▲ =k，▲为x，●为y，◆为z，
∴k=x+y-z+zy+x+y+x=x+y2x+y=12，
∴x=12y,y-z=12x,z=12x+y，
∴y=2x,z=32x，
∴▲，●，◆这三种物体的重量比为2:4:3．
故选：B．
【点拨】考查比例性质的应用；利用等比性质得到所给比值的确定值是解决本题的关键．
【变式5-1】（2023·上海虹口·统考一模）已知x:y=3:2，那么x-y:x= ．
【答案】1:3
【分析】本题考查了比例的性质，表示出y是解题的关键．先用x表示出y，再代入比例式进行计算即可得解．
【详解】解：∵x:y=3:2，
∴y=23x，
∴x-y:x=x-23x:x=13x:x=1:3，
故答案为：1:3．
【变式5-2】（2023·宁夏银川·校考一模）若ba=dc=12a≠c，则2b-d2a-c= ．
【答案】12/0.5
【分析】根据等比性质、合比性质转换即可．
【详解】解：∵ba=dc=12a≠c，
∴2b2a=dc=12a≠c，
∴2b-d2a-c=12a≠c，
故答案为12．
【点拨】本题考查了比例线段，比例的性质，正确理解等比性质、合比性质是解题的关键．
【变式5-3】（2023·江西抚州·校联考一模）解方程：
(1)xx-3=2x-6；
(2)已知a:b:c=2:3:4，且2a+3b-2c=15，求a-2b+3c的值．
【答案】(1)x1=3，x2=2；
(2)24
【分析】（1）先移项，再利用因式分解法解一元二次方程，此题得解；
（2）由a:b:c=2:3:4，可设a=2k，则b=3k，c=4k，根据2a+3b-2c=15可得出关于k的一元一次方程，解之即可得出k值，进而可得出a，b，c的值，将其代入a-2b+3c中即可求出结论．
【详解】（1）解：移项得，xx-3-2x-3=0，
即x-3x-2=0，
即x-3=0或x-2=0，
解得：x1=3，x2=2；
（2）解：∵a:b:c=2:3:4，
∴设a=2k，则b=3k，c=4k．
∵2a+3b-2c=15，
∴4k+9k-8k=15，
解得：k=3，
∴a=6，b=9，c=12，
∴a-2b+3c=6-18+36=24．
【点拨】本题考查了因式分解法解一元二次方程、解一元一次方程以及比例的性质，解题的关键是：（1）熟练掌握因式分解法解一元二次方程的解法；（2）根据比例关系结合2a+3b-2c=15列出关于k的一元一次方程．
【变式5-4】（2023·安徽·校联考模拟预测）已知2ab+c+d=2ba+c+d=2ca+b+d=2da+b+c=k，求k2-3k-4的值．
【答案】-509或6．
【分析】当a+b+c+d≠0时，依据等比性质可得2(a+b+c+d)3(a+b+c+d)=k，当a+b+c+d=0时，得b+c+d=﹣a，代入即可计算出k的值．
【详解】∵2ab+c+d=2ba+c+d=2ca+b+d=2da+b+c=k，
∴当a+b+c+d≠0时，由等比性质可得，2(a+b+c+d)3(a+b+c+d)=k，
k=2(a+b+c+d)3(a+b+c+d)=23；
当a+b+c+d=0时，b+c+d=﹣a，
∴k=2ab+c+d=2a-a=-2；
当k=23时，k2-3k-4=232-3×23-4=- 509；
当k=-2时，k2-3k-4=-22-3×-2-4=6．
【点拨】本题主要考查了比例的性质的运用，解决问题的关键是掌握比例的性质．
题型06 理解黄金分割的概念
【例6】（2023·上海杨浦·统考一模）已知P是线段AB的黄金分割点，且AP>BP，那么下列等式能成立的是（ ）
A．ABAP=APBPB．ABBP=BPAP
C．APBP=5-12D．ABAP=5-12
【答案】A
【分析】本题考查黄金分割点，根据黄金分割点的定义得出线段比例关系，选出正确选项，解题的关键是掌握黄金分割点的性质．
【详解】解：如图，
∵点P是线段AB的黄金分割点，且AP>BP，
∴APAB=PBAP=5-12，
故选：A．
【变式6-1】（2023·河南郑州·统考二模）神奇的自然界中处处蕴含着数学知识．如图是古希腊时期的帕提农神庙（Parthenn Temple），我们把图中的虚线表示为矩形ABCD，并发现AD:DC≈0.618，这体现了数学中的（ ）

A．平移B．旋转C．轴对称D．黄金分割
【答案】D
【分析】根据黄金分割比可得答案．
【详解】解：∵AD:DC≈0.618，
∴体现了数学中的黄金分割；
故选D
【点拨】本题考查的是黄金分割比的含义，熟记黄金分割比为5-12≈0.618是解本题的关键．
【变式6-2】（2023·四川成都·校考三模）已知点C为线段AB的黄金分割点，AC>BC．若AC=6 cm，则AB的长为 cm．
【答案】35+3/3+35
【分析】利用黄金比例列出方程解答即可．
【详解】解：∵点C为线段AB的黄金分割点，
∴ACAB=5-12，
∴6AB=5-12，
∴AB=35+3．
故答案为：35+3．
【点拨】本题考查了黄金分割点的应用，正确应用黄金比是解答本题的关键．
题型07 黄金分割的实际应用
【例7】（2023·云南昆明·统考二模）如果矩形ABCD满足ABBC=5-12，那么矩形ABCD叫做“黄金矩形”，如图，已知矩形ABCD是黄金矩形，对角线AC，BD相交于O且BC=2，则关于黄金矩形ABCD，下列结论不正确的是（ ）
A．AC=BDB．
C．AC=8-25D．矩形ABCD的周长C=25+2
【答案】C
【分析】计算得出AB=5-1，根据矩形的性质求得各项，即可判断．
【详解】解：∵ABBC=5-12，且BC=2，
∴AB=5-1，
∵四边形ABCD是矩形，
∴AC=BD，故选项A正确，不符合题意；
∴S△AOB=14S矩形ABCD=14×2×5-1=5-12，故选项B正确，不符合题意；
∴AC=5-12+22=10-25≠8-25，故选项C错误，符合题意；
∴矩形ABCD的周长C=25-1+2=25+2，故选项D正确，不符合题意；
故选：C．
【点拨】本题考查了矩形的性质，二次根式的混合运算，掌握二次根式的混合运算法则是解题的关键．
【变式7-1】（2023·陕西西安·陕西师大附中校考模拟预测）如图，点C是线段AB的黄金分割点，即BCAC=ACAB，若S1表示以CA为一边的正方形的面积，S2表示长为AB，宽为CB的矩形的面积，则S1与S2的大小关系是（ ）
A．S1>S2B．S12（舍去）或x=3-5，
检验，当x=3-5时，原分式方程有意义，
∴x=3-5，即AC=3-5，
∴BC=2-3-5=5-1，
∴该雕像的下部设计高度为5-1m，
故答案为：5-1．
【点拨】本题主要考查比例，解比例方程，理解题意，掌握比例的性质，解比例方程是解题的关键．
【变式7-3】（2023·江西鹰潭·统考二模）【课本再现】黄金分割是一种最能引起美感的分割比例，具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值、我们知道：如图1，如果BCAC=ACAB，那么称点C为线段AB的黄金分割点．

(1)【问题发现】如图1，请直接写出CB与AC的比值是___________；
(2)【尺规作黄金分割点】如图2，在Rt△ABC中，∠C=90°，BC=1，AC=2，在BA上截取BD=BC，在AC上截取AE=AD，求AEAC的值；
(3)【问题解决】如图3，用边长为4的正方形纸片进行如下操作：对折正方形ABDE得折痕MN，连接EN，点A对应点H，得折痕CE，试说明：C是AB的黄金分割点．
【答案】(1)5-12
(2)5-12
(3)见解析
【分析】（1）由BCAC=ACAB得到CB⋅AB=AC2，由AB=AC+CB，代入后整理得到CBAC2+CBAC-1=0，解方程即可得到答案；
（2）在Rt△ABC中，∠C=90°，BC=1，AC=2，由勾股定理得，AB=5，由BD=BC=1得到AD=AB-BD=5-1，则AE=AD=5-1，即可得到AEAC的值；
（3）设EC与MN相交于点P，作PQ⊥EN于点Q，由MN∥AB，MN=AB，且M为AE的中点得到MPAC=EMAE=12，EM=12AE=2，可得到PQ=MP=12AC，设PQ=MP=12AC=x，则PN=4-x，由勾股定理得到EN=25，由sin∠ENM=PQPN=EMEN得到x4-x=225，解得x=5-1，则AC=25-2，求出ACAB=5-12，BCAC=5-12，即可得到结论．
【详解】（1）解：∵BCAC=ACAB，
∴CB⋅AB=AC2，
∵AB=AC+CB，
∴CB⋅AC+CB=AC2，
整理得，CB2+CB⋅AC-AC2=0，
两边同除以AC2得，CBAC2+CBAC-1=0，
解得CBAC=5-12，CBAC=-5-12（不合题意，舍去），
∴CB与AC的比值是5-12，
故答案为：5-12
（2）在Rt△ABC中，∠C=90°，BC=1，AC=2，
由勾股定理得，AB=AC2+BC2=22+12=5，
∵BD=BC=1，
∴AD=AB-BD=5-1，
∴AE=AD=5-1，
∴AEAC=5-12，
即AEAC的值为5-12；
（3）设EC与MN相交于点P，作PQ⊥EN于点Q，

∵MN∥AB，MN=AB，且M为AE的中点，
∴MPAC=EMAE=12，EM=12AE=2，
∵EC平分∠AEN，
∴PQ=MP=12AC，
设PQ=MP=12AC=x，
则PN=MN-PM=4-x，
∵EN=EM2+MN2=22+42=25，
∴sin∠ENM=PQPN=EMEN，
∴x4-x=225，
解得x=5-1，
经检验x=5-1是分式方程的根，
∴AC=2x=25-2，
∴ACAB=25-24=5-12，
BCAC=4-25-225-2=5-12，
∴BCAC=ACAB=5-12，
∴C是AB的黄金分割点．
【点拨】此题考查了平行线分线段成比例定理、锐角三角函数、折叠的性质、勾股定理、正方形的性质、解方程等知识，正确做出辅助线是解题的关键．
【变式7-4】（2023·湖北孝感·校考模拟预测）阅读：两千多年前，古希腊数学家欧多克索斯发现了黄金分割，即：点P是线段AB上一点(AP>BP)，若满足BPAP=APAB，则称点P是AB的黄金分割点．黄金分割在我们的数学学习中也处处可见，比如我们把有一个内角为36°的等腰三角形称为“黄金三角形”．

(1)应用：如图1，若点C是线段AB的黄金分割点(AC>BC)，若AB=1，则AC的长为 ______．
(2)运用：如图2，已知等腰三角形ABC为“黄金三角形”，AB=AC，∠A=36°，BD为∠ABC的平分线．求证：点D是AC的黄金分割点．
(3)如图3中，AB=AC，∠A=36°，BF平分∠ABC交AC于F，取AB的中点E，连接EF并延长交BC的延长线于M．BC=1，请你直接写出CM的长为__________．
【答案】(1)5-12
(2)证明见解析
(3)
【分析】（1）设AC=a，则BC=1-a，根据黄金分割的含义可得：BCAC=ACAB，即AC2=BC·AB，再解方程即可；
（2）证明△CBD∽△CAB，推出CDBC=BCAC，推出CDAD=ADAC，可得结论．
（3）如图，连接AM，同理可得：∠ABC=∠ACB=72°，∠1=∠2=36°=∠BAC，可得AF=BF=BC=1，证明ME⊥AB，MB=MA，∠CAM=72°-36°=36°=∠BAC，可得C是BM的黄金分割点，且BCBC)，AB=1，
设AC=a，则BC=1-a，
∴BCAC=ACAB，即AC2=BC·AB，
∴a2=1-a，
∴a2+a-1=0，
解得：a=5-12（负根舍去），
∴AC=5-12；
（2）证明：∵AB=AC，∠A=36°，
∴∠ABC=∠C=72°，
又∵BD平分∠ABC，
∴∠ABD=∠CBD=12∠ABC=36°，
∴∠BDC=36°+36°=72°，
∴AD=BD，BC=BD， 即AD=BD=BC，
又∵∠C=∠C，∠CBD=∠A，
∴△CBD∽△CAB，
∴ CDBC=BCAC ，
∴CDAD=ADAC ，
∴D点是AC的黄金分割点．
（3）如图，连接AM，
同理可得：∠ABC=∠ACB=72°，∠1=∠2=36°=∠BAC，
∴AF=BF=BC=1，
∵E为AB的中点，AF=BF，
∴ME⊥AB，
∴MB=MA，

∴∠ABM=∠BAM=72°，∠AMB=36°，
∴∠CAM=72°-36°=36°=∠BAC，
同理可得C是BM的黄金分割点，且BC