2023年山东省东营市九年级数学中考复习考前适应性综合模拟预测题(原卷版+解析版)
展开一、选择题(共30分)
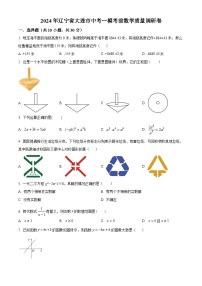
1. 下列图形既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2. 下列计算中,结果正确的是( )
A. B. C. D.
3. 将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )
A. 43°B. 47°
C. 30°D. 60°
4. 某物体的三个视图如图所示,该物体的直观图是( )
A. B. C. D.
5. 将抛物线y=x2-4x+5的顶点A向左平移2个单位长度得到点,则点的坐标是( )
A. (2,3)B. (2,-1)C. (4,1)D. (0,1)
6. 已知在同一直角坐标系中二次函数和反比例函数的图象如图所示,则一次函数的图象可能是( )
A B. C. D.
7. 一个圆锥的侧面展开图是半径为6、圆心角为120°的扇形,那么这个圆锥的底面圆的半径为( )
A 1B. 2C. 3D. 4
8. 某工程队铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设x米,根据题意可列方程为( )
A. B.
C. D.
9. 一个盒子里有完全相同的三个小球,球上分别标上数字1、2、4.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程有两个不相等实数根的概率是( )
A. B. C. D.
10. 如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有()
A. 5个B. 4个C. 3个D. 2个
二、填空题(共28分)
11. 国务院总理温家宝在政府工作报告中指出,我国2012年国内生产总值51.9万亿元.51.9万亿元用科学记数法表示为_________元.
12. 因式分解:a3﹣2a2b+ab2=_____.
13. 某中学足球队9名队员的年龄情况如下:
则该队队员年龄的众数和中位数分别是__________
14. 如图,的顶点与坐标原点重合,,,当点在反比例函数的图象上移动时,点坐标满足的函数解析式为_________.
15. 若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是___.
16. 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为_______米.
17. 如图,在中,,,,是内部一动点,且满足,则长的最小值是________.
18. 如图,已知直线l:,过点作x轴的垂线交直线l于点,在线段右侧作等边三角形,过点作x轴的垂线交x轴于,交直线l于点,在线段右侧作等边三角形,按此作法继续下去,则的坐标为 _____;的坐标为 _____. (n为正整数)
三、解答题(共62分.)
19. (1)计算: ;
(2)先化简,再求代数式的值,其中x是不等式组的整数解.
20. 为迎接2020年第35届全国青少年科技创新大赛,某学校举办了A:机器人;B:航模;C:科幻绘画;D:信息学;E:科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.
根据统计图中信息解答下列问题:
(1)本次参加比赛的学生人数是_________名;
(2)把条形统计图补充完整;
(3)求扇形统计图中表示机器人的扇形圆心角的度数;
(4)在C组最优秀的3名同学(1名男生2名女生)和E组最优秀的3名同学(2名男生1名女生)中,各选1名同学参加上一级比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.
21 如图,直线y=mx+n与双曲线y=相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C.
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积.
22. 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若AC=8,tan∠DAC=,求⊙O的半径.
23. 为切实做好新冠疫情防控工作,我区某校准备在药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.
(1)求每盒口罩和每盒水银体温计的价格各是多少元?
(2)如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.
24. 提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
25. 已知,经过点的抛物线与x轴相交于点及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作轴,垂足为H,平行于y轴的直线交线段于点Q,交抛物线于点P,当四边形为平行四边形时,求的度数;
(3)如图2,试探究:在抛物线上是否存在点C,使?若存在,请求出直线解析式;若不存在,请说明理由.
年龄(单位:岁)
14
15
16
17
人数
1
4
2
2
2023年广西中考考前最后一卷数学模拟预测题(原卷版+解析版): 这是一份2023年广西中考考前最后一卷数学模拟预测题(原卷版+解析版),文件包含2023年广西中考考前最后一卷数学模拟预测题原卷版docx、2023年广西中考考前最后一卷数学模拟预测题解析版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。
2023年山东省临沂市九年级数学中考复习考前适应性综合模拟预测题(原卷版+解析版): 这是一份2023年山东省临沂市九年级数学中考复习考前适应性综合模拟预测题(原卷版+解析版),文件包含2023年山东省临沂市九年级数学中考复习考前适应性综合模拟预测题原卷版docx、2023年山东省临沂市九年级数学中考复习考前适应性综合模拟预测题解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
2024年山东省淄博市九年级中考数学模拟预测题(原卷版+解析版): 这是一份2024年山东省淄博市九年级中考数学模拟预测题(原卷版+解析版),文件包含2024年山东省淄博市九年级中考数学模拟预测题原卷版docx、2024年山东省淄博市九年级中考数学模拟预测题解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。