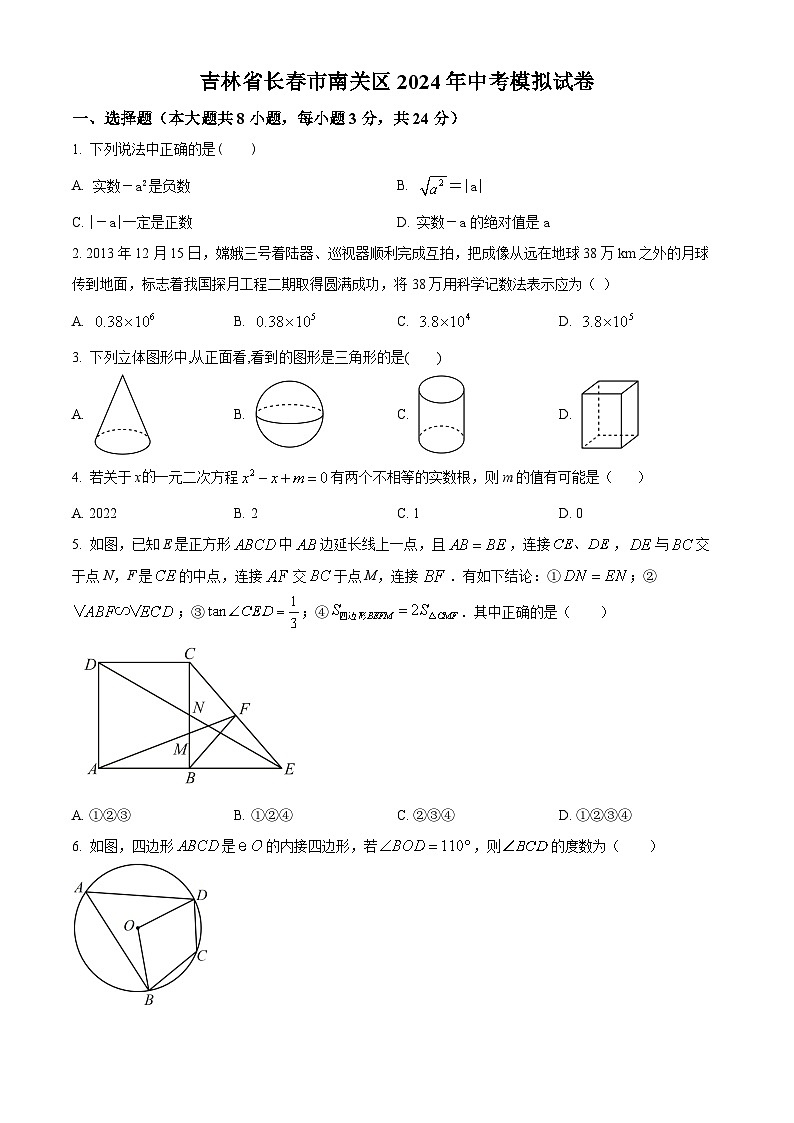
2024年吉林省长春市南关区中考数学模拟预测题（原卷版+解析版）

这是一份2024年吉林省长春市南关区中考数学模拟预测题（原卷版+解析版），文件包含2024年吉林省长春市南关区中考数学模拟预测题原卷版docx、2024年吉林省长春市南关区中考数学模拟预测题解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
1. 下列说法中正确的是( )
A. 实数－a2是负数B. ＝|a|
C. |－a|一定是正数D. 实数－a的绝对值是a
【答案】B
【解析】
【详解】实数是负数或零，选项A错误；
=|a|，选项B正确；
是正数或零，选项C错误；
实数绝对值是，选项D错误.
故选B.
2. 2013年12月15日，嫦娥三号着陆器、巡视器顺利完成互拍，把成像从远在地球38万km之外的月球传到地面，标志着我国探月工程二期取得圆满成功，将38万用科学记数法表示应为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
【详解】解：依题意，38万
故选：D．
3. 下列立体图形中,从正面看,看到的图形是三角形的是( )
A. B. C. D.
【答案】A
【解析】
【详解】试题分析：A．圆锥主视图是三角形，符合题意；
B．球的主视图是圆，不符合题意；
C．圆柱的主视图是矩形，不符合题意；
D．正方体的主视图是正方形，不符合题意．
故选A．
考点：简单几何体的三视图．
4. 若关于x的一元二次方程有两个不相等的实数根，则m的值有可能是（ ）
A. 2022B. 2C. 1D. 0
【答案】D
【解析】
【分析】根据判别式的意义得到△=（1）24m＞0，然后解关于m的不等式，最后对各选项进行判断．
【详解】解：∵关于x的一元二次方程x2﹣x+m＝0有两个不相等的实数根
∴判别式,
又∵，
∴，
解得，
∴m的值可能是0；
故选：D．
【点睛】本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程无实数根．
5. 如图，已知E是正方形中边延长线上一点，且，连接，与交于点N，F是的中点，连接交于点M，连接．有如下结论：①；②；③；④．其中正确的是（ ）
A. ①②③B. ①②④C. ②③④D. ①②③④
【答案】D
【解析】
【分析】根据“角角边”，证明，根据全等三角形的性质，得到，判断①；根据两边对应成比例、夹角相等的两个三角形相似判断②；作于G，根据等腰直角三角形的性质、正切的定义求出，根据相似三角形的性质判断③；根据三角形的面积公式计算，判断④．
【详解】解：∵四边形为正方形，，
∴，
∴，
又∵
∴，
∴，故①结论正确；
∵是的中点，
∴，
∴，
∴，
∴，
∵，
∴，
∴，故②结论正确；
作于G，则，
∴，
∴，
∵，
∴，
∴，故③结论正确；
∵，
，
，
，
∵F是的中点，
∴，
∴，故④结论正确；
故选：D．
【点睛】本题主要考查了正方形的性质，等腰直角三角形的性质，相似三角形的判定与性质，全等三角形的判定与性质，正确证明两三角形相似是解答本题的关键．
6. 如图，四边形是的内接四边形，若，则的度数为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据圆周角定理求出的度数，再根据圆内接四边形的性质求解即可．
【详解】解：由圆周角定理得，，
∵四边形为的内接四边形，
∴．
故选：B．
【点睛】本题主要考查了圆内接四边形的性质、圆周角定理，掌握圆内接四边形的对角互补是解题的关键．
7. 等腰三角形的一个角是，则它的底角是（ ）
A. B. 或C. 或D.
【答案】B
【解析】
【分析】本题主要考查等腰三角形的性质，分两种情况讨论是解题的关键．
分这个角为底角和顶角两种情况，根据等腰三角形的性质及三角形的内角和求解即可．
【详解】解：当底角为时，则底角为，
当顶角为时，底角为：，
所以底角为或．
故答案为：B．
8. 如图，抛物线y=ax2+bx+c的对称轴是直线x=1．下列结论：
①abc＜0；②b2－4ac＞0；③当x＞0时，y随x的增大而减小；④8a+c＜0；⑤5a+b+2c＞0．
其中正确结论的个数是（ ）
A. 1B. 2C. 3D. 4
【答案】D
【解析】
【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
【详解】由图象可知a＜0，b＞0，c＞0，b2－4ac＞0故②正确；
∴abc＜0，①正确；
当x＞1时，y随x的增大而减小，故③错误；
∵对称轴是直线x=1
∴
∴b=-2a
∴8a+c=4a+4a+c=4a-2b+c
∵当x=-2时，y=4a-2b+c＜0
∴8a+c＜0，故④正确；
∵5a+b+2c=5a-2a+2c=3a+2c=a+2a+c+c=a-b+c+c
∵当x=-1时，y=a-b+c＞0，c＞0，
∴a-b+c+c＞0，故⑤正确；
故选D．
【点睛】本题考查了二次函数的图象与系数的关系，还考查了同学们从函数图象中获取信息的能力，以及考查二次函数的图象和性质．
二、填空题（本大题共6小题，每小题3分，共18分）
9. 分解因式：______．
【答案】
【解析】
【分析】本题考查提公因式法和公式法综合因式分解，分解因式要彻底是解题的关键．
先提公因式，再利用平方差公式分解即可．
【详解】解：原式；
故答案为： ．
10. 若一元一次不等式组的解集为x>a,则a的取值范围是______.
【答案】
【解析】
【分析】由不等式组的解集为x>a, 根据“同大取大”可知.
【详解】解：∵一元一次不等式组的解集为x>a,
∴，
故答案为.
【点睛】本题考查了含参数的一元一次不等式组，对于端点值的确定是解题关键.
11. 正八边形的内角和等于______．
【答案】##1080度
【解析】
【分析】本题考查了多边形的内角和，熟记多边形的内角和公式是解题的关键，根据正多边形的内角和公式即可得到求出答案．
【详解】∵边形内角和
∴正八边形的内角和
12. 如图，以O为位似中心将四边形放大后得到四边形，若，则四边形和四边形的周长的比为________．
【答案】1:2
【解析】
【分析】由以为位似中心将四边形放大后得到四边形，若，可求得四边形和四边形的位似比，继而求得四边形和四边形的周长的比．此题考查了位似变换与相似多边形的性质．注意位似就是相似，相似三角形的周长的比等于相似比．
【详解】解：以为位似中心将四边形放大后得到四边形，
四边形和四边形的位似比为：，
四边形和四边形的周长的比为：．
故答案为：．
13. 如图，在中，，，，将绕点逆时针旋转后得到，则图中阴影部分的面积是______．
【答案】
【解析】
【分析】先利用含30度的直角三角形三边的关系计算出，，再根据旋转的性质得到，，，则，接着在中计算出，从而得到，然后根据扇形的面积公式，利用图中阴影部分的面积进行计算．
【详解】解：，，
，，，
将绕点逆时针旋转后得到，
，，，
，
在中，
，
，
，
图中阴影部分的面积．
故答案为．
【点睛】本题考查了扇形面积计算：设圆心角是，圆的半径为R的扇形面积为S，则 或（其中l为扇形的弧长）．求阴影面积的主要思路是将不规则图形面积转化为规则图形的面积．也考查了旋转的性质．
14. 如图，在平面直角坐标系中，一条直线与反比例函数（x＞0）的图象交于两点A、B，与x轴交于点C，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数（x＞0）的图象交于两点D、E，连接DE，则四边形ABED的面积为____．
【答案】．
【解析】
【详解】∵点A、B在反比例函数（x＞0）的图象上，设点B的坐标为（，m），
∵点B为线段AC的中点，且点C在x轴上，
∴点A的坐标为（，2m）．
∵AD∥x轴、BE∥x轴，且点D、E在反比例函数（x＞0）的图象上，
∴点D的坐标为（，2m），点E的坐标为（，m），
∴S梯形ABED==．
故答案为．
三、解答题（本大题共10小题，共78分）
15. 先化简，再求值：，其中x为方程的根．
【答案】1
【解析】
【分析】先将除式括号里面的通分后，将除法转换成乘法，约分化简．然后解一元二次方程，根据分式有意义的条件选择合适的x值，代入求值．
【详解】解：原式＝．
解得，
，
∵时，无意义，
∴取．
当时，原式＝．
16. 《算法统宗》是我国古代数学名著之一，其中记载了这样的数学问题：“用绳子测水井深度，绳长的三分之一比井深多4尺；绳长的四分之一比井深少1尺，问绳长、井深各是多少尺？”．若设这个问题中的绳长为x尺，求x的值．
【答案】60
【解析】
【分析】设绳长x尺，则井深为（）尺或（），可得方程，解方程即可．
【详解】解：设绳长为x尺，则井深为（）尺或（）尺，
则，
解得：x＝60，
答：x的值为60．
【点睛】本题考查了一元一次方程的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程求解．
17. 如图，在平行四边形中，对角线，并于点，经过点的直线交于，交于F．
（1）求证：．
（2）连接，，则与满足什么条件时，四边形是矩形？请说明理由．
【答案】（1）见解析 （2）时，四边形为矩形，见解析
【解析】
【分析】此题考查了平行四边形的性质，全等三角形的判定与性质，以及矩形的判定，熟练掌握平行四边形的性质是解本题的关键．
（1）由平行四边形的对边平行且相等，得到与平行，利用两直线平行内错角相等得到两对角相等，再由对角线互相平分得到，利用得到三角形与三角形全等，利用全等三角形对应边相等即可得证；
（2）与相等时，四边形是矩形，理由为：由与平行且相等得到四边形为平行四边形，利用对角线互相平分的平行四边形是矩形即可得证．
【小问1详解】
证明：平行四边形，
，，
，，
在和中，
，
，
；
【小问2详解】
解：若时，四边形为矩形，理由为：
，
，
，
四边形为平行四边形，
，
四边形为矩形．
18. 甲、乙、丙、丁四人玩扑克牌游戏，他们先取出两张红心和两张黑桃共四张扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色的即为游戏搭档，现甲、乙两人各抽取了一张，求两人恰好成为游戏搭档的概率．（请用“画树状图”或“列表”等方法写出分析过程）
【答案】．
【解析】
【详解】试题分析：利用列举法即可列举出所有各种可能的情况，然后利用概率公式即可求解．
试题解析：根据题意画图如下：
共有12中情况，从4张牌中任意摸出2张牌花色相同颜色4种可能，所以两人恰好成为游戏搭档的概率=．
考点：列表法与树状图法．
19. 如图，在的方格纸巾，请按要求画图．
（1）在图1中画一个格点C，使为等腰三角形．
（2）在图2中画两个格点F，G，使四边形为中心对称图形，且对角线互相垂直．
【答案】（1）见解析；
（2）见解析
【解析】
【分析】（1）根据等腰三角形的概念作图即可（答案不唯一）；
（2）根据中心对称图形的概念及菱形、正方形的性质作图即可（答案不唯一）．
【小问1详解】
解：如图1所示，△ABC即为所求（答案不唯一）．
【小问2详解】
解：如图2所示，四边形DEFG即为所求（答案不唯一）．
【点睛】本题主要考查作图，解题的关键是掌握旋转变换的定义与性质、等腰三角形的定义、菱形与正方形的性质．
20. 当前各国都高度重视人工智能并视其为提升国家竞争力重要力量，随着人工智能与各个垂直领域的不断深入融合，普通公民也越来越需要具备人工智能的基本知识和应用能力，人工智能逐步成为中小学重要教学内容之一，某同学设计了一款机器人，为了了解它的操作技能情况，对同一设计动作与人工进行了比赛，机器人和人工各操作次，测试成绩（百分制）如下：

分析数据，得到下列表格．
根据以上信息，解答下列问题：
（1）填空： ， ， ．
（2）若成绩分及以上为优秀，请你估计机器人操作次，优秀次数为多少？
（3）根据以上数据分析，请你写出机器人在操作技能方面的优点． (写一条即可)
【答案】（1）；；
（2）估计机器人操作次，优秀次数约为次
（3）答案不唯一，见解析
【解析】
【分析】此题主要考查了方差和众数、中位数，样本估计总体，以及利用方差做决策，关键是掌握三数定义和方差的计算公式．
（1）分别根据中位数、众数以及方差的定义解答即可；
（2）先计算出优秀所占的比例，再乘即可；
（3）根据统计表数据解答即可．
【小问1详解】
把机器人数据从小到大排列，排在中间的两个数分别是和，故中位数；
在人工数据中，出现的次数最多，故众数；
机器人的方差，
故答案为：；；；
【小问2详解】
次．
答：估计机器人操作次，优秀次数约为次；
【小问3详解】
机器人的样本数据的平均数高于人工，方差较小，可以推断其优势在于操作技能水平较高的同时还能保持稳定．
21. 设与成正比例，且当时，．求与之间函数关系式．
【答案】
【解析】
【分析】根据题意设，将与的值代入求出的值，即可确定出与关系式．此题考查了待定系数法求一次函数解析式，以及一次函数图象上点的坐标特征，熟练掌握待定系数法是解本题的关键．
【详解】解：与成正比例，
设，
代入，，得，
解得，
，
即．
22. 综合与实践
【问题情境】
通过查看出厂包装袋上的数据，数学活动小组的同学发现纸的长与宽分别为和，其比值为，而，他们上网查阅资料也发现纸的长与宽的比是一个特殊值“”．不妨定义长与宽的比为的矩形为“标准矩形”．
【操作实践】
如图1，数学活动小组的同学在几何画板软件上画了一个正方形，连接对角线，在射线上截取了，过点E作交的延长线于点F，令．
【问题探究】
（1）求证：四边形为“标准矩形”．
（2）如图2，数学活动小组的同学在图1的基础上隐藏了线段，在线段上取一点P，连接，．
①当平分时，求的长；
②当的周长最小时，求的正切值．
【答案】（1）见解析 （2）①；②
【解析】
【分析】（1）由已知得，可证得，得证．
（2）①由，，可得，得，，设，由得，解出即可．
②延长BF至点，使得，连接，交EF于点P，连接PB，则此时的周长最小，由轴对称的性质，得，所以，分别求出，长即可．
【小问1详解】
证明：∵四边形ABCD是正方形，
∴，．
∴．
∴．
∴．
∴四边形为“标准矩形”．
【小问2详解】
①解：∵DP平分，
∴．
又∵，，
∴（SAS）．
∴，．
∵，，
∴．
∴．
∴是等腰直角三角形．
∴．
设，则．
∴，
解得．
∴．
②解：延长BF至点，使得，连接，交EF于点P，连接PB，如解图所示，则此时的周长最小．
∵，，
∴．
∴．
由轴对称的性质，得．
∴．
【点睛】本题考查了几何变换的综合应用，涉及的知识点有勾股定理，全等三角形的判定和性质，应用轴对称求三角形的周长最短，锐角三角函数值的求法．熟练掌握相关的知识，添加适当的辅助线进行转化是关键．
23. 图1是某学校存放学生自行车的车棚的示意图（尺寸如图所示），车棚顶部是圆柱侧面的一部分，其展开图是矩形．图2是车棚顶部截面的示意图，所在圆的圆心为O．车棚顶部是用一种帆布覆盖的，求覆盖棚顶的帆布的面积．（不考虑接缝等因素，计算结果保留π）
【答案】帆布的面积为160π平方米．
【解析】
【分析】连接OB、过点O作OE⊥AB、垂足为E、交于F，先根据垂径定理得到EF是弓形高，进而求得AE=2,EF=2; 设半径为R米，则OE＝（R﹣2）米，然后运用勾股定理列方程求得R，可得OA的长；再根据sin∠AOE，从而求得∠AOE=60°，即∠AOB=120°,最后根据弧长公式和扇形面积公式解答即可．
【详解】解：如图：连接OB，过点O作OE⊥AB，垂足为E，交于F，，
∵E是AB中点，F是中点，
∴EF是弓形高，
∴AEAB＝2，EF＝2，
设半径为R米，则OE＝（R﹣2）米，
在Rt△AOE中，由勾股定理，得R2＝（R﹣2）2+（2）2，解得R＝4，
∵sin∠AOE，
∴∠AOE＝60°，
∴∠AOB＝120度．
∴的长为π（m），
∴帆布的面积为π×60＝160π（平方米）．
【点睛】本题主要考查圆的垂径定理、勾股定理、锐角三角函数、弧长公式以及扇形的面积公式，灵活利用相关知识点成为解答本题的关键．
24. 如图，抛物线y＝－x 2＋bx＋c与x轴交于A、B两点，与y轴交于点C，已知经过B、C两点的直线的表达式为y＝－x＋3．
(1)求抛物线的函数表达式；
(2)点P(m，0)是线段OB上的一个动点，过点P作y轴的平行线，交直线BC于D，交抛物线于E，EF∥x轴，交直线BC于F，DG∥x轴，FG∥y轴，DG与FG交于点G．设四边形DEFG的面积为S，当m为何值时S最大，最大值是多少？
(3)在坐标平面内是否存在点Q，将△OAC绕点Q逆时针旋转90°，使得旋转后的三角形恰好有两个顶点落在抛物线上．若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．
【答案】（1）y＝－x 2＋2x＋3 （2）当m＝ 时，S有最大值 （3）存在符合条件的点Q，点Q的坐标为（ ，）或（ ，）
【解析】
【详解】试题分析：（1）先求出直线与x轴和y轴的交点坐标，再代入抛物线解析式中，即可求得抛物线的解析式；
（2）由P坐标可表示D、E点坐标，进而表示出DE长，由二次函数的最值可求得当DE去最大值时m的值，由于四边形DEFG为正方形，所以面积为DE 2，即可求得S的最大值；
（3）分两种情况讨论：①当点A′、C′ 落在抛物线上时；②当点O′、C′ 落在抛物线上时，
即可求得点Q的坐标.
试题解析：（1）在y＝－x＋3中，令y＝0，得x＝3；令x＝0，得y＝3，
∴B（3，0），C（0，3）
∵抛物线y＝－x 2＋bx＋c经过B、C两点
∴
解得
∴抛物线的函数表达式为y＝－x 2＋2x＋3；
（2）∵P（m，0），PD∥y轴交直线BC于D，交抛物线于E
∴D（m，－m＋3），E（m，－m 2＋2m＋3）
∴DE＝－m 2＋2m＋3－( －m＋3 )＝－m 2＋3m＝－( m－ )2＋
∴当m＝ 时，DE有最大值 ，
由题意可知四边形DEFG为矩形
∵OB＝OC＝3，
∴∠DBP＝∠BDP＝∠EDF＝∠EFD＝45°
∴DE＝EF∴四边形DEFG为正方形
∴S＝DE 2
∴当m＝ 时，S有最大值 ；
（3）如图所示，有两种情况：
①当点A′、C′ 落在抛物线上时
由O′A′＝OA＝1，O′C′＝OC＝3
设A′（a，－a 2＋2a＋3），则C′（a－3，－a 2＋2a＋4）
∴－a 2＋2a＋4＝－( a－3 )2＋2( a－3 )＋3
解得a＝ ，∴A′（，）
作QN⊥x轴于N，A′M⊥QN于M，连接QA、QA′
则∠AQA′＝90°，可证△QAN≌△A′QM
设Q（x，y），则QM＝AN＝x＋1
A′M＝QN＝y＝x＋1＋ ＝ －x
解得x＝ ，y＝
∴Q1（ ，）
②当点O′、C′ 落在抛物线上时
则O′、C′ 两点关于抛物线的对称轴对称，易知抛物线的对称轴为直线x＝1，
由O′C′＝OC＝3，可知C′（－ ，），
作QN⊥O′C′ 于N，CM⊥QN于M，连接QC、QC′
则∠CQC′＝90°，
可证△CQM≌△QC′N，
设Q（x，y），则QM＝C′N＝x＋
CM＝QN＝y－ ＝x＝3－( x＋ )－
解得x＝ ，y＝
∴Q2（ ，）
综上所述，存在符合条件的点Q，点Q的坐标为（ ，）或（ ，）
点睛：本题考查二次函数综合题、待定系数法、旋转变换等知识，解题的关键是雪狐构建二次函数，利用二次函数的性质解决最值问题，学会分类讨论，属于压轴题.
平均数
中位数
众数
方差
机器人
人工