初中数学北师大版七年级下册3 探索三角形全等的条件评课课件ppt

这是一份初中数学北师大版七年级下册3 探索三角形全等的条件评课课件ppt，共21页。PPT课件主要包含了本节目录，不一定全等，“边边边”判定方法，几何语言，解题思路，先找现有条件，ABAC，再找隐含条件，公共边AD，最后找准备条件等内容，欢迎下载使用。
1.(2022新课标)掌握基本事实：三边分别相等的两个三角形全等.2.(2022新课标)了解三角形的稳定性.3.在探索三角形全等条件及其应用过程中，能够进行有条理的思考并进行简单的推理.
几何直观　推理能力 模型观念　应用意识
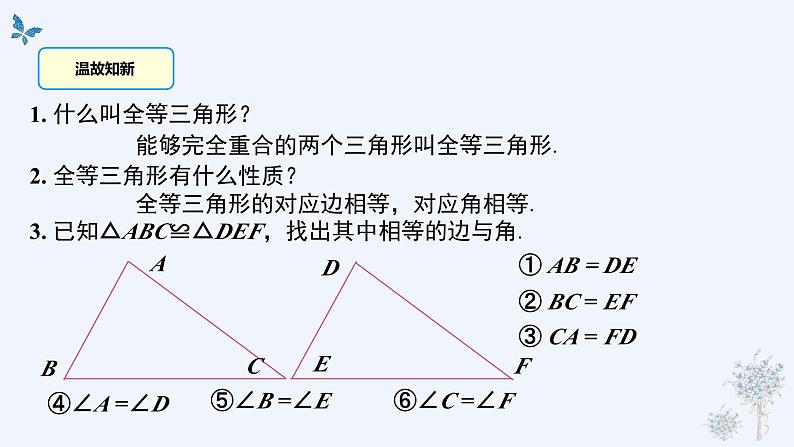
1. 什么叫全等三角形？
能够完全重合的两个三角形叫全等三角形.
3. 已知△ABC≌△DEF，找出其中相等的边与角.
2. 全等三角形有什么性质？
全等三角形的对应边相等，对应角相等.
猜一猜：(1)只给出一个条件或两个条件，能否保证所画出的三角形一定全等？答：_____.
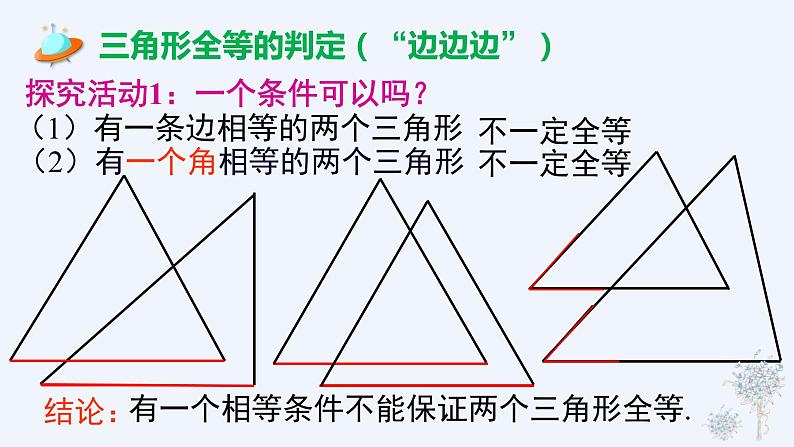
探究活动1：一个条件可以吗？
（1）有一条边相等的两个三角形
（2）有一个角相等的两个三角形
有一个相等条件不能保证两个三角形全等.
三角形全等的判定（“边边边”）
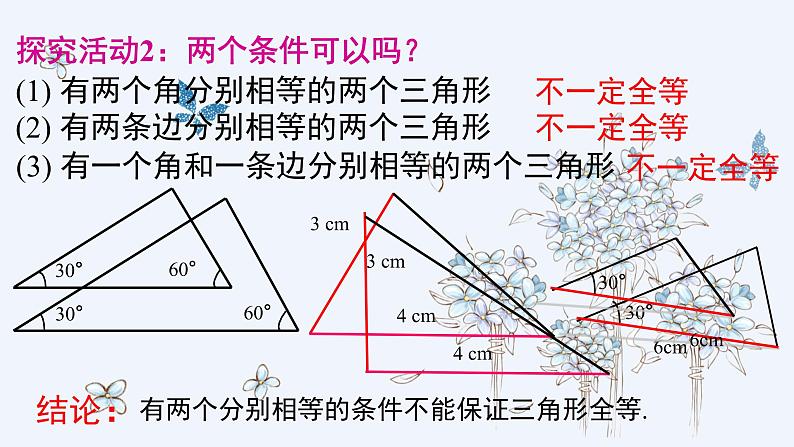
有两个分别相等的条件不能保证三角形全等.
探究活动2：两个条件可以吗？
(1) 有两个角分别相等的两个三角形
(2) 有两条边分别相等的两个三角形
(3) 有一个角和一条边分别相等的两个三角形
猜一猜：(1)只给出一个条件或两个条件，能否保证所画出的三角形一定全等？答：_____.(2)如果给定三个条件画三角形，共有几种可能？答：_______、_______、_________和_________,共4种情况.
第1课时 利用“边边边”判定三角形全等
文字语言：三边分别相等的两个三角形全等， 简写为“边边边”或“SSS”.
在△ABC 和△DEF 中，
所以△ABC≌△DEF（SSS）.
例1 如图，有一个三角形钢架，AB = AC，AD 是连接点 A 与 BC 中点 D 的支架.试说明：(1)△ABD≌△ACD；
解：因为 D 是 BC 中点， 所以 BD = DC． 在△ABD 与△ACD 中，
所以△ABD≌△ACD (SSS).
(2)∠BAD =∠CAD.
解：由（1）得△ABD≌△ACD，所以 ∠BAD = ∠CAD（全等三角形对应角相等）.
如图，C 是 BF 的中点，AB = DC，AC = DF.试说明：△ABC≌△DCF.
在△ABC 和△DCF 中，
所以△ABC≌△DCF
解：因为 C 是 BF 中点，
所以 BC = CF.
知识点二：三角形的稳定性
“只要三角形三条边的长度确定了，这个三角形的形状和大小也就完全确定了”，三角形的这个性质叫做“三角形的稳定性”. 这就是说，三角形的稳定性不是“拉得动、拉不动”的问题，其实质应是“三角形的三边长一旦确定，其形状和大小就唯一确定了”.
三角形的稳定性在实际生活中有着广泛的应用，如钢架桥、房屋架梁等，因此要使一些图形具有稳定的结构，往往通过连接辅助线转化为三角形而获得.
1. (北师7下P98、人教8上P6)如图，三角形具有　 　，四边形具有　 　.
2.工人师傅在安装木制门框时，为防止变形常常如上图所示，钉上两条斜拉的木条，这样做的原理是根据三角形的______性.
3.(2022广东)下列图形中有稳定性的是( )A.三角形 B.平行四边形C.长方形 D.正方形
4.(跨学科融合)(北师7下P98、人教8上P7)在实际生活中，我们经常利用一些几何图形的稳定性或不稳定性，下列实物图中利用了稳定性的是( )
5.【例2】(跨学科融合)我们用如图所示的方法(斜钉上一块木条)来修理一条摇晃的凳子的数学原理是利用三角形的　 　.
6. 如图，桥梁的斜拉钢索是三角形的结构，主要是为了（ ） A. 节省材料，节约成本 B. 保持对称 C. 利用三角形的稳定性 D. 美观漂亮
6. 如图，AB = AC，DB = DC，请说明∠B =∠C 成立的理由.
在△ABD 和△ACD 中，
AB = AC (已知)，
DB = DC (已知)，
AD = AD (公共边)，
所以∠B =∠C (全等三角形的对应角相等).
7. 已知 AC = AD，BC = BD，试说明：AB 是∠DAC 的平分线.
AC = AD ( )，
BC = BD ( )，
AB = AB ( )，
所以△ABC≌△ABD ( ).
所以 AB 是∠DAC 的平分线
(全等三角形的对应角相等).
解：在△ABC 和△ABD 中，