江苏省徐州市丰县2023-2024学年七年级下学期期中数学模拟试卷

这是一份江苏省徐州市丰县2023-2024学年七年级下学期期中数学模拟试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）下列计算中，正确的是（ ）
A．（a2）3＝a5B．a8÷a2＝a4C．（2a）3＝6a3D．a2+a2＝2a2
2．（3分）下列各式能用平方差公式计算的是（ ）
A．（2a+b）（2b﹣a）B．（﹣m﹣n）（﹣m+n）
C．（x+1）（﹣x﹣1）D．（3x﹣y）（﹣3x+y）
3．（3分）已知三角形的两边分别为2和6，则此三角形的第三边可能是（ ）
A．2B．4C．6D．8
4．（3分）若M＝（x﹣2）（x﹣5），N＝（x﹣3）（x﹣4），则M与N的大小关系为（ ）
A．M＞NB．M＝N
C．M＜ND．由x的取值而定
5．（3分）如图，已知四边形ABCD，当满足什么条件时AB∥CD（ ）
A．∠A＝∠BB．∠A+∠B＝180°
C．∠B+∠C＝180°D．∠C+∠D＝180°
6．（3分）下列多项式能进行因式分解的是（ ）
A．2a2﹣2B．a2﹣2a+4C．a2+1D．a2﹣a+2
7．（3分）如图，直线a，b被直线c，d所截．下列条件能判定a∥b的是（ ）
A．∠1＝∠3B．∠2+∠4＝180°该试卷源自 每日更新，提供24小时找卷服务，全网性价比高。 C．∠4＝∠5D．∠1＝∠2
8．（3分）如图，在四边形ABCD中，∠A+∠D＝α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P＝（ ）
A．90°﹣αB．90°+αC．D．360°﹣α
二、填空题（本大题共10小题，每小题4分，共40分）
9．（4分）防尘口罩会阻隔小于0.0000025米的呼吸性粉尘，从而起到过滤空气的作用，其中0.0000025用科学记数法表示为 ．
10．（4分）若am＝2，an＝3，则am+2n＝ ．
11．（4分）如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法，其理由是 ．
12．（4分）若代数式x2+ax+16是一个完全平方式，则a＝ ．
13．（4分）若（x﹣a）（3x﹣2）的积中不含x的一次项，则a的值为 ．
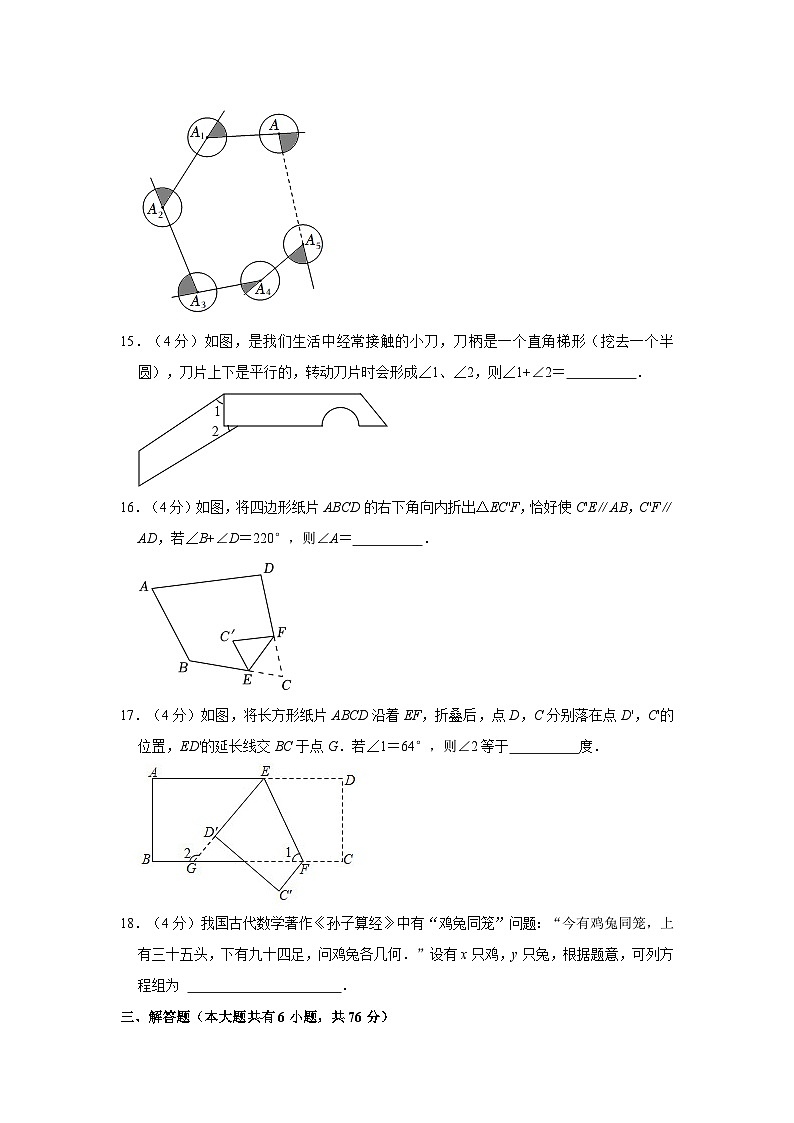
14．（4分）如图所示，分别以n边形的顶点为圆心，以3cm为半径画圆，则图中阴影部分的面积之和为 ．
15．（4分）如图，是我们生活中经常接触的小刀，刀柄是一个直角梯形（挖去一个半圆），刀片上下是平行的，转动刀片时会形成∠1、∠2，则∠1+∠2＝ ．
16．（4分）如图，将四边形纸片ABCD的右下角向内折出△EC'F，恰好使C'E∥AB，C'F∥AD，若∠B+∠D＝220°，则∠A＝ ．
17．（4分）如图，将长方形纸片ABCD沿着EF，折叠后，点D，C分别落在点D'，C'的位置，ED'的延长线交BC于点G．若∠1＝64°，则∠2等于 度．
18．（4分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设有x只鸡，y只兔，根据题意，可列方程组为 ．
三、解答题（本大题共有6小题，共76分）
19．（12分）计算：
（1）3a2b•（﹣2ab）3；
（2）（x+3y）（2x﹣y）．
20．（12分）因式分解：
（1）4m2﹣9n2；
（2）9a2b﹣6ab2+b3．
21．（13分）如图，点B、C在直线AD上，∠ABE＝40°，BF平分∠DBE，CG∥BF，求∠DCG的度数．
22．（13分）如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．
（1）通过观察，可以发现△ABC是 ．
A．锐角三角形
B．钝角三角形
C．直角三角形
D．直角三角形或锐角三角形
（2）仅利用无刻度的直尺画出△ABC的中线AD与角平分线CE；
（3）△ABC的面积为 ，△ABD的面积为 ．
23．（13分）如图，将一个边长为a的正方形图形分割成四部分（两个正方形和两个长方形），请认真观察图形，解答下列问题：
（1）请用两种方法表示该图形阴影部分的面积（用含a、b的代数式表示）：
①方法一： ；方法二： ；
（2）若图中a、b满足a2+b2＝31，ab＝3，求阴影部分正方形的边长；
（3）若（2021﹣y）（2023﹣y）＝1010，求（2021﹣y）2+（2023﹣y）2的值．
24．（13分）如图1，大运河某河段的两岸AB、CD安置了两座可旋转探照灯M、N假设河道两岸平行（即AB∥CD），灯M光从MB开始顺时针旋转至MA便立即回转，灯N光束从NC开始顺时针旋转至ND便立即回转，两灯不停照射巡逻．灯M转动的速度是每秒1度，灯N转动的速度是每秒2度，灯M转动的时间为t秒．
（1）若灯M光束先转动30秒后，灯N光束才开始转动．
①直接写出灯M光束和灯N光束， 灯先回转；（填M或N）
②在灯M光束到达MA之前，当两灯的光束平行时，求t的值；
（2）如图2，连接MN，且∠BMN＝2∠MND．
①直接写出∠MND＝ ；
②若两灯同时转动，在灯N到达ND之前，若两灯光束交于点E，在转动过程中，请探究∠BME与∠MEF的之间数量关系？并说明理由．
参考答案与试题解析
一、选择题（本大题共8小题，每小题3分，共24分．下列各题的四个选项中，只有一项是正确的，请在答题卡上将正确选项的对应字母涂黑）
1．（3分）下列计算中，正确的是（ ）
A．（a2）3＝a5B．a8÷a2＝a4C．（2a）3＝6a3D．a2+a2＝2a2
【解答】解：A、（a2）3＝a6，故A不符合题意；
B、a8÷a2＝a6，故B不符合题意；
C、（2a）3＝8a3，故C不符合题意；
D、a2+a2＝2a2，故D符合题意；
故选：D．
2．（3分）下列各式能用平方差公式计算的是（ ）
A．（2a+b）（2b﹣a）B．（﹣m﹣n）（﹣m+n）
C．（x+1）（﹣x﹣1）D．（3x﹣y）（﹣3x+y）
【解答】A、此选项中不存在互为相同或相反的项，不能用平方差公式计算，故本选项不合题意；
B、﹣m是相同的项，互为相反项是n与﹣n，符合平方差公式的要求，故本选项符合题意；
C、不存在相同的项，不能用平方差公式计算，故本选项不合题意；
D、不存在相反的项，不能用平方差公式计算，故本选项不合题意；
故选：B．
3．（3分）已知三角形的两边分别为2和6，则此三角形的第三边可能是（ ）
A．2B．4C．6D．8
【解答】解：4＜第三边＜8，在这个范围内的只有C．
故选：C．
4．（3分）若M＝（x﹣2）（x﹣5），N＝（x﹣3）（x﹣4），则M与N的大小关系为（ ）
A．M＞NB．M＝N
C．M＜ND．由x的取值而定
【解答】解：∵M＝（x﹣2）（x﹣5）
＝x2﹣5x﹣2x+10
＝x2﹣7x+10；
N＝（x﹣3）（x﹣4）
＝x2﹣4x﹣3x+12
＝x2﹣7x+12，
∴M﹣N＝x2﹣7x+10﹣（x2﹣7x+12）
＝x2﹣7x+10﹣x2+7x﹣12
＝﹣2＜0，
∴M＜N．
故选：C．
5．（3分）如图，已知四边形ABCD，当满足什么条件时AB∥CD（ ）
A．∠A＝∠BB．∠A+∠B＝180°
C．∠B+∠C＝180°D．∠C+∠D＝180°
【解答】解：A．∵∠A与∠B是同旁内角，∠A＝∠B，不能判断两直线平行，不符合题意；
B．∵∠A+∠B＝180°，
∴AD∥BC，不符合题意；
C．∵∠B+∠C＝180°，
∴AB∥CD，符合题意，
D．∵∠C+∠D＝180°，
∴AD∥BC，不符合题意；
故选：C．
6．（3分）下列多项式能进行因式分解的是（ ）
A．2a2﹣2B．a2﹣2a+4C．a2+1D．a2﹣a+2
【解答】解：A、2a2﹣2＝2（a+1）（a﹣1），故符合题意．
B、a2﹣2a+4不能分解因式，故不符合题意．
C、a2+1，不能分解因式，故不符合题意．
D、a2﹣a+2不能分解因式，故不符合题意．
故选：A．
7．（3分）如图，直线a，b被直线c，d所截．下列条件能判定a∥b的是（ ）
A．∠1＝∠3B．∠2+∠4＝180°
C．∠4＝∠5D．∠1＝∠2
【解答】解：A、当∠1＝∠3时，c∥d，故此选项不合题意；
B、当∠2+∠4＝180°时，c∥d，故此选项不合题意；
C、当∠4＝∠5时，c∥d，故此选项不合题意；
D、当∠1＝∠2时，a∥b，故此选项符合题意；
故选：D．
8．（3分）如图，在四边形ABCD中，∠A+∠D＝α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P＝（ ）
A．90°﹣αB．90°+αC．D．360°﹣α
【解答】解：∵四边形ABCD中，∠ABC+∠BCD＝360°﹣（∠A+∠D）＝360°﹣α，
∵PB和PC分别为∠ABC、∠BCD的平分线，
∴∠PBC+∠PCB＝（∠ABC+∠BCD）＝（360°﹣α）＝180°﹣α，
则∠P＝180°﹣（∠PBC+∠PCB）＝180°﹣（180°﹣α）＝α．
故选：C．
二、填空题（本大题共10小题，每小题4分，共40分）
9．（4分）防尘口罩会阻隔小于0.0000025米的呼吸性粉尘，从而起到过滤空气的作用，其中0.0000025用科学记数法表示为 2.5×10﹣6 ．
【解答】解：0.0000025＝2.5×10﹣6．
故答案为：2.5×10﹣6．
10．（4分）若am＝2，an＝3，则am+2n＝ 18 ．
【解答】解：am+2n＝am•a2n＝am•（an）2＝2×9＝18．
故答案为：18．
11．（4分）如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法，其理由是 同位角相等，两直线平行 ．
【解答】解：由图形得，有两个相等的同位角存在，
所以依据：同位角相等，两直线平行，即可得到所得的直线与已知直线平行．
故答案为：同位角相等，两直线平行．
12．（4分）若代数式x2+ax+16是一个完全平方式，则a＝ ±8 ．
【解答】解：∵x2+ax+16是一个完全平方式，
∴a＝±8．
故答案为：±8．
13．（4分）若（x﹣a）（3x﹣2）的积中不含x的一次项，则a的值为 ﹣ ．
【解答】解：（x﹣a）（3x﹣2）＝3x2﹣（3a+2）x+2a，
由结果不含x的一次项，得到3a+2＝0，
解得：a＝﹣，
故答案为﹣．
14．（4分）如图所示，分别以n边形的顶点为圆心，以3cm为半径画圆，则图中阴影部分的面积之和为 9πcm2 ．
【解答】解：由图可得，
阴影部分所对的圆心角之和为360°，
∴图中阴影部分的面积之和为：π×32＝9π（cm2），
故答案为：9πcm2．
15．（4分）如图，是我们生活中经常接触的小刀，刀柄是一个直角梯形（挖去一个半圆），刀片上下是平行的，转动刀片时会形成∠1、∠2，则∠1+∠2＝ 90° ．
【解答】解：如图，过点O作OP∥AB，则∠1＝∠AOP．
∵AB∥CD，
∴OP∥CD，
∴∠2＝∠POC，
∵∠AOP+∠POC＝90°，
∴∠1+∠2＝90°，
故答案为：90°
16．（4分）如图，将四边形纸片ABCD的右下角向内折出△EC'F，恰好使C'E∥AB，C'F∥AD，若∠B+∠D＝220°，则∠A＝ 70° ．
【解答】解：∵C'E∥AB，C'F∥AD，
∴∠D＝∠C'FC，∠B＝∠C'EC，
∵∠B+∠D＝220°，
∴∠C'FC+∠C'EC＝220°，
∵∠C'+∠C'FC+∠C'EC+∠C＝360°，
∴∠C'+∠C＝140°，
∵∠C'＝∠C，
∴∠C＝70°，
∵∠A+∠B+∠C+∠D＝360°，
∴∠A＝70°，
故答案为：70°．
17．（4分）如图，将长方形纸片ABCD沿着EF，折叠后，点D，C分别落在点D'，C'的位置，ED'的延长线交BC于点G．若∠1＝64°，则∠2等于 128 度．
【解答】解：∵AD∥BC，∠1＝64°，
∴∠DEF＝∠1＝64°，
由折叠的性质可得：∠FEG＝∠DEF＝64°，
∴∠2＝∠1+∠FEG＝64°+64°＝128°．
故答案为：128．
18．（4分）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何．”设有x只鸡，y只兔，根据题意，可列方程组为 ．
【解答】解：由题意可得，．
故答案为：．
三、解答题（本大题共有6小题，共76分）
19．（12分）计算：
（1）3a2b•（﹣2ab）3；
（2）（x+3y）（2x﹣y）．
【解答】解：（1）3a2b•（﹣2ab）3
＝3a2b•（﹣8a3b3）
＝﹣24a5b4；
（2）（x+3y）（2x﹣y）
＝2x2﹣xy+6xy﹣3y2
＝2x2+5xy﹣3y2．
20．（12分）因式分解：
（1）4m2﹣9n2；
（2）9a2b﹣6ab2+b3．
【解答】解：（1）原式（2m）2﹣（3n）2
＝（2m+3n）（2m﹣3n）；
（2）原式＝b（9a2﹣6ab+b2）
＝b（3a﹣b）2．
21．（13分）如图，点B、C在直线AD上，∠ABE＝40°，BF平分∠DBE，CG∥BF，求∠DCG的度数．
【解答】解：∵∠ABE＝40°，
∴∠DBE＝180°﹣40°＝140°，
∵BF平分∠DBE，
∴，
∵CG∥BF，
∴∠DCG＝∠DBF，
∴∠DCG＝70°．
22．（13分）如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．
（1）通过观察，可以发现△ABC是 C ．
A．锐角三角形
B．钝角三角形
C．直角三角形
D．直角三角形或锐角三角形
（2）仅利用无刻度的直尺画出△ABC的中线AD与角平分线CE；
（3）△ABC的面积为 12 ，△ABD的面积为 6 ．
【解答】解：（1）由格点可知，∠C＝45°+45°＝90°，
∴△ABC是直角三角形，
故选：C；
（2）∵D为线段BC的中点，作图如下，
由（1）可知∠ACB＝90°，CE为∠C的平分线，作图如下：
（3）由题意知，
∴，
故答案为：12，6．
23．（13分）如图，将一个边长为a的正方形图形分割成四部分（两个正方形和两个长方形），请认真观察图形，解答下列问题：
（1）请用两种方法表示该图形阴影部分的面积（用含a、b的代数式表示）：
①方法一： （a﹣b）2 ；方法二： a2﹣2ab+b2 ；
（2）若图中a、b满足a2+b2＝31，ab＝3，求阴影部分正方形的边长；
（3）若（2021﹣y）（2023﹣y）＝1010，求（2021﹣y）2+（2023﹣y）2的值．
【解答】解：（1）①该图形阴影部分的面积为（a﹣b）2；②该图形阴影部分的面积为a2﹣2ab+b2
故答案为：（a﹣b）2；a2﹣2ab+b2
（2）（a﹣b）2＝a2﹣2ab+b2＝31﹣6
＝25，
∴a﹣b＝5（负值舍去）
答：阴影部分正方形的边长是5；
（3）设2021﹣y＝m，2023﹣y＝n，
则mn＝1010，m﹣n＝﹣2，
∴m2+n2＝（m﹣n）2+2mn，
＝（﹣2）2+2×1010
＝4+2020
＝2024．
∴（2021﹣y）2+（2023﹣y）2＝2024．
24．（13分）如图1，大运河某河段的两岸AB、CD安置了两座可旋转探照灯M、N假设河道两岸平行（即AB∥CD），灯M光从MB开始顺时针旋转至MA便立即回转，灯N光束从NC开始顺时针旋转至ND便立即回转，两灯不停照射巡逻．灯M转动的速度是每秒1度，灯N转动的速度是每秒2度，灯M转动的时间为t秒．
（1）若灯M光束先转动30秒后，灯N光束才开始转动．
①直接写出灯M光束和灯N光束， N 灯先回转；（填M或N）
②在灯M光束到达MA之前，当两灯的光束平行时，求t的值；
（2）如图2，连接MN，且∠BMN＝2∠MND．
①直接写出∠MND＝ 60° ；
②若两灯同时转动，在灯N到达ND之前，若两灯光束交于点E，在转动过程中，请探究∠BME与∠MEF的之间数量关系？并说明理由．
【解答】解：（1）①N．
灯M转到MA的时间（秒），
灯N转到ND的时间为（秒），可知90＜150，
所以灯N先回转；
故答案为：N；
②当灯N回转前，如图，
由题意：∠BMH＝t°，∠CNG＝2（t﹣30）°．
∵AB∥CD，
∴∠BGN＝∠CNG＝2（t﹣30）°．
∵MH∥NG，
∴∠BGN＝∠BMH，
∴2（t﹣30）＝t，
解得t＝60．
当灯N回转后，如图，
由题意：∠BMH＝t，∠DNG＝2（t﹣30）﹣180，
∵AB∥CD，
∴∠DNG＝∠AGN＝2（t﹣30）﹣180．
∵MH∥NG，
∴∠BMH+∠AGN＝180°，
∴t+2（t﹣30）﹣180＝180，
解得t＝140．
答：t的值为60s或140s；
（2）①∵AB∥CD，
∴∠BMN+∠MND＝180°，
即2∠MND+∠MND＝180°，
解得∠MND＝60°．
故答案为：60°；
②∠BME＝∠MEF．理由是：
由①知∠MND＝60°，
∴∠CNM＝180°﹣∠MND＝120°．
设两灯同时运动xs，
则∠BME＝x，∠CNE＝2x，
∴∠EMN＝∠BMN﹣∠BME＝120﹣x，∠MNE＝∠CNE﹣∠MNC＝2x﹣120，
∴∠MEF＝∠EMN+∠MNE＝120﹣x+2x﹣120＝x，
∴∠BME＝∠MEF．