2024年安徽省宿州市宿城第一初级中学中考三模数学试题（含解析）

这是一份2024年安徽省宿州市宿城第一初级中学中考三模数学试题（含解析），共24页。试卷主要包含了化简的结果正确的是，如图，是的外接圆，等内容，欢迎下载使用。

1．你拿到的试卷满分为150分，考试时间为120分钟．
2．本试卷包括“试题卷”和“答题卷”两部分．“试题卷”共4页，“答题卷”共6页．
3．请务必在“答题卷”上答题，在“试题卷”上答题是无效的．
4．考试结束后，请将“试题卷”和“答题卷”一并交回．
一、选择题（本大题共10小题，每小题4分，满分40分）
每小题都给出A、B、C、D四个选项，其中只有一个是符合题目要求的．
1．比小4的数是（ ）
A．1B．C．D．6
2．2023年末，安徽省耕地面积约8342万亩，较上年增加约15万亩，实现连续3年净增加．数据8342万用科学记数法表示为（ ）
A．B．C．D．
3．下列运算正确的是（ ）
A．B．
C．D．
4．七个大小相同的正方体搭成的几何体如图所示，则该几何体的俯视图是（ ）
A．B．C．D．
5．化简的结果正确的是（ ）
A．2B．C．D．
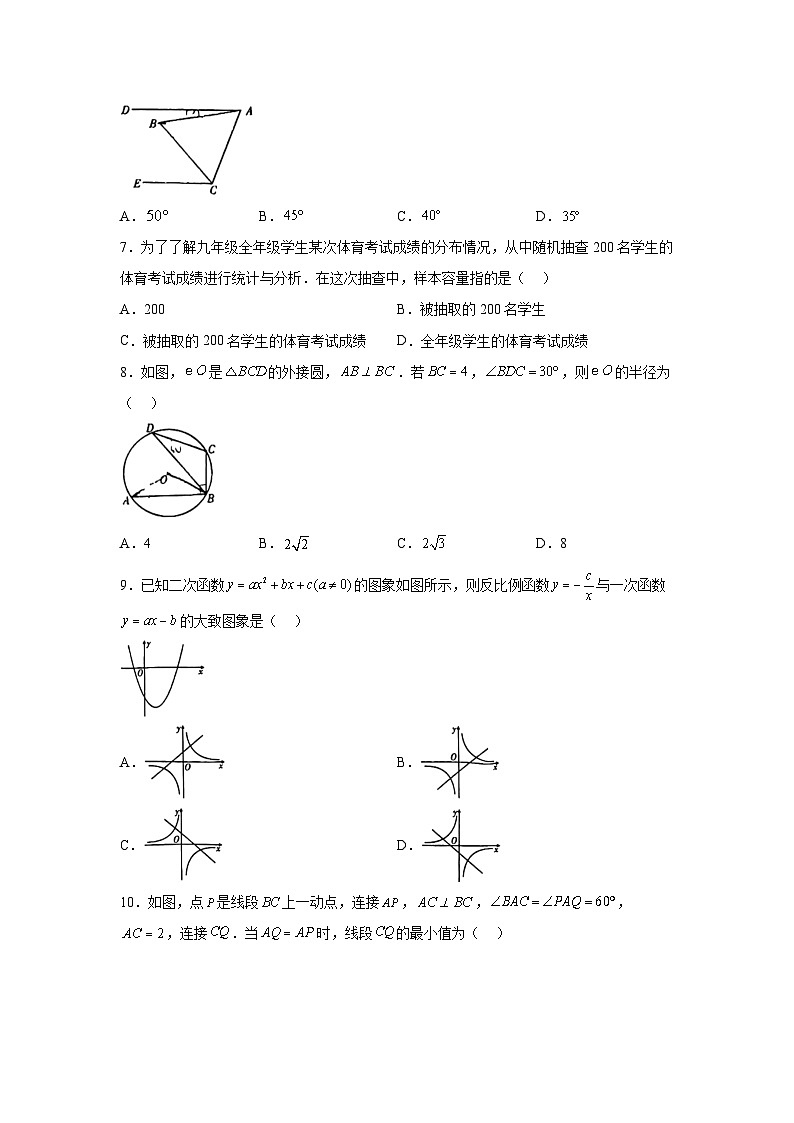
6．如图，是等边三角形，，，则的度数为（ ）
A．B．C．D．
7．为了了解九年级全年级学生某次体育考试成绩的分布情况，从中随机抽查200名学生的体育考试成绩进行统计与分析．在这次抽查中，样本容量指的是（ ）
A．200B．被抽取的200名学生
C．被抽取的200名学生的体育考试成绩D．全年级学生的体育考试成绩
8．如图，是的外接圆，．若，，则的半径为（ ）
A．4B．C．D．8
9．已知二次函数的图象如图所示，则反比例函数与一次函数的大致图象是（ ）
A．B．
C．D．
10．如图，点是线段上一动点，连接，，，，连接．当时，线段的最小值为（ ）
A．B．1C．D．2
二、填空题（本大题共4小题，每小题5分，满分20分）
11．分解因式：＝ ．
12．若关于的一元二次方程有实数根，则实数可取的最小整数值是 ．
13．如图，在四边形中，平分，点，分别是，的中点．若，，则的长为 ．

14．如图，，连接，反比例函数与分别交于，两点．
（1）当点的坐标为时，反比例函数的表达式为 ．
（2）连接，记的面积为．若，则的取值范围为 ．
三、（本大题共2小题，每小题8分，满分16分）
15．计算：．
16．某商场购进一批某品牌上衣A、两种型号共80件，其进价和售价如下表，
该商场预计获得利润不少于6000元．请问至少购进A型号上衣多少件？
四、（本大题共2小题，每小题8分，满分16分）
17．如图，在由边长为1个单位长度的小正方形组成的网格中，已知的顶点都在格点上，直线与网线重合．
(1)以直线为对称轴，画出关于对称的；
(2)将向右平移10个单位长度，再向上平移1个单位长度，得到，画出，并连接、，直接判断四边形的形状．
18．观察下列图形与等式的关系：
第1个图
第2个图
第3个图
第4个图
……
根据图形及等式的关系，解决下列问题：
(1)第5个图中空白部分小正方形的个数是______，第6个图中空白部分小正方形的个数满足的算式：______；
(2)用含的等式表示第个图中空白部分小正方形的个数反映的规律：______；
(3)运用上述规律计算：．
五、（本大题共2小题，每小题10分，满分20分）
19．如图，是的直径，，过点作的切线，交的延长线于点，连接交于点．
(1)求证：；
(2)若，，求的长．
20．光线从一种介质进入另一种介质时会发生折射现象．如图1，我们把称为折射率（法线与介质相互垂直）．操作一：如图2，在一个无水的水槽中，有一束激光恰好落在水槽点处．操作二；如图3，保持激光的角度和高度不变，在水槽中加入一定量的水，水平面为，这束光发生折射，光线与交于点，折射光线为，为法线．已知四边形是矩形，该束光从空气到水中的折射率，，入射角，求的长．（参考数据：，，）

六、（本题满分12分）
21．某校八、九年级开展了以“心理健康”为主题的知识竞赛，现随机抽取八、九年级各10名学生的测试成绩进行整理分析，收集到的数据及制成不完整的表格如下：
八年级10名学生测试成绩分别为：，，，，，，，，，．
九年级10名学生测试成绩分别为：，，，，，，，，，
根据上述信息，解答下列问题：
(1)______，______；
(2)请判断八、九年级中，学生测试成绩较稳定的是几年级？并说明理由；
(3)学校从中评选出表现突出的四名学生，其中有两名男生．现准备从表现突出的学生中随机选取两名学生分享体会，请用画树状图或列表的方法求所选学生中有男生的概率．
七、（本题满分12分）
22．如图1，矩形矩形，点是上一点，，，三点共线．
(1)已知，求的长；
(2)将矩形围绕点按逆时针方向旋转，过点作交于点，其他条件不变．
（i）如图2，求证：；
（ii）如图3，与交于点，延长交于点，求证：．
八、（本题满分14分）
23．如图1，抛物线与轴交于点与点，点位于点的左侧，与轴交于点，．
(1)求，的值；
(2)点是第一象限内且位于该抛物线上一点．
（i）如图2，连接与交于点，连接．若点与点关于抛物线的对称轴对称，求点的坐标；
（ii）如图3，点是第四象限且位于该抛物线上一点，与分别与轴交于点和点．若，则直线恒经过一点，求该点的坐标．
型号
进价（元/件）
售价（元/件）
260
340
220
280
平均数
众数
中位数
八年级
90
94
九年级
90
92.5
1．C
【分析】本题考查有理数的减法运算，正确的翻译句子，列出算式进行计算即可．
【详解】解：比小4的数是；
故选C．
2．B
【分析】本题主要考查了科学记数法，将数据表示成形式为的形式，其中，n为整数，正确确定a、n的值是解题的关键．
先将8342万写成，然后再写成其中，n为整数的形式即可．
【详解】解：8342万．
故选B．
3．D
【分析】本题主要考查了积的乘方、完全平方公式、合并同类项、同底数幂除法等知识点，熟练掌握运算法则是解答本题的关键．
根据积的乘方、完全平方公式、合并同类项、同底数幂除法逐项判断即可．
【详解】解：A. ，故选项A错误，不符合题意；
B. ，故选项B错误，不符合题意；
C. 和不是同类项，不能合并，故选项C错误，不符合题意；
D. ，故选项D正确，符合题意．
故选：D．
4．B
【分析】本题主要考查了组合体的三视图，掌握从上面看到的图形是几何体的俯视图成为解题的关键．
根据从上面看到的图形是几何体的俯视图即可解答．
【详解】解：从上面看，一共有三列，第一列有两个小正方形，第二列有两个小正方形，第三列有一个小正方形．即主视图为：
．
故选B．
5．B
【分析】本题主要考查了分式的加减运算，掌握异分母分式的加减运算法则是解题的关键．直接运用异分母分式的加减运算法则计算即可．
【详解】解：．
故选：B．
6．A
【分析】本题主要考查了等边三角形的性质、平行线的性质等知识点，灵活运用相关性质成为解题的关键．
根据等边三角形的性质可得，即，再根据平行线的性质可得，最后根据角的和差即可解得．
【详解】解：∵是等边三角形，
∴，
∴，
∵，
∴，
∴．
故选A．
7．A
【分析】本题主要考查了总体、个体与样本的定义，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．
【详解】解：在这次抽查中，样本容量指的是
故选：A．
8．A
【分析】本题考查圆周角定理，含30度角的直角三角形，连接，根据直角所对的弦为直径，以及同弧所对的圆周角相等，得到为直径，，进而求出的长即可．
【详解】解：连接，则：，
∵，
∴，
∴为的直径，
∵，，，
∴，
∴的半径为；
故选A．
9．A
【分析】本题主要考查了一次函数的图象、反比例函数的图象、二次函数的图象等知识点，根据函数图象确定相关参数的正负成为解题的关键．根据一次函数与反比例函数图象确定a、b、c的正负，再结合二次函数图象的对称轴即可解答．
【详解】解：由图可知二次函数开口向上、对称轴在轴右侧、与y轴的交点在负半轴，
则，则；
∴，则一次函数的图象过一、二、三象限；
，则反比例函数图象在一、三象限，
∴A选项的图象符合题意，
故选：A．
10．B
【分析】本题主要考查了全等三角形的判定和性质、含角的直角三角形的性质等知识点，找出点P和点F重合时，最小，最小值为的长度是解本题的关键．
如图：在上取一点E，使，连接，过点E作于F，由，证明，由全等三角形的性质得出，则当（点P和点F重合）时，最小，然后由含角的直角三角形的性质即可解答．
【详解】解：如图：在上取一点E，使，连接，过点E作于F，
∵，，
∴，
∴，
∴，
∴，
又∵，，
∴，
∴，
要使最小，则有最小，而点E是定点，点P是上的动点，
∴当（点P和点F重合）时，最小，即点P与点F重合，最小，最小值为的长度，
在中，，，
∴，
∵，
∴，
在中，，
∴，故线段长度的最小值是1，
故选：B．
11．
【分析】本题主要考查了分解因式，先提取公因式再利用公式法即可得到答案．
【详解】解：，
故答案为：．
12．
【分析】本题主要考查了一元二次方程根的判别式，，掌握一元二次方程根的判别式与根的关系成为解题的关键．
根据一元二次方程根的判别式列出不等式求解即可．
【详解】解：∵关于的一元二次方程有实数根，
∴，即，解得：
∴k的最小整数值为．
故答案为：．
13．
【分析】本题考查三角形的中位线定理，勾股定理，取的中点，连接，根据三角形的中位线定理，求出的长，得到，利用勾股定理求出的长即可．
【详解】解：∵，
∴，
∵平分，
∴，
∴，
取的中点，连接，

∵点，分别是，的中点，
∴，
∴，
∴，
∵，
∴，
∴，
∴；
故答案为：．
14．
【分析】本题考查反比例函数与一次函数的交点问题：
（1）先求出直线的解析式，进而求出点坐标，待定系数法求出反比例函数的表达式即可；
（2）根据三角形的面积公式，求出的范围，进而求出的取值范围即可．
【详解】解：（1）∵，
∴，
设直线的解析式为，把，代入，得：，
∴，
当时，，
∴，
∴，
∴；
故答案为：．
（2）∵，
∵，
∴，
∵，
∴当时，，当时，，
∴，即：；
故答案为：．
15．
【分析】本题考查了实数的混合运算，根据化简绝对值，二次根式的性质化简，特殊角的三角函数值，负整数指数幂进行计算即可求解．
【详解】解：
16．商场至少购进A型号上衣60件．
【分析】本题主要考查了一元一次不等式的应用，审清题意、找准不等关系、正确列出一元一次不等式是解题的关键．
设至少购进A型号上衣x件，则购进B型号上衣件，再根据预计获得利润不少于6000元不等式求解即可．
【详解】解：设至少购进A型号上衣x件，则购进B型号上衣件，
根据题意可得：，解得：，
答：商场至少购进A型号上衣60件．
17．(1)见解析
(2)见解析，四边形为平行四边形
【分析】（1）根据轴对称的性质画图即可；
（2）根据平移的性质画出图形，再根据平行四边形的判定，即可解答．
【详解】（1）解：如图所示．
（2）解：如图所示．
根据题意得：，
∴四边形为平行四边形．
【点睛】本题考查了作图轴对称和平移，平行四边形的判定，解题关键是掌握轴对称和平移的性质，平行四边形的判定定理．
18．(1)11，
(2)
(3)2025
【分析】本题考查图形变化的规律，有理数的混合运算等知识点，
（1）根据题图找出规律即可得解；
（2）根据题图找出规律即可得解；
（2）根据题图找出的规律计算即可得解；
能根据所给等式写出图n空白部分小正方形个数满足的等式是解题的关键．
【详解】（1）解：由图知：第5个空白小正方形的个数为，第6个空白小正方形的个数算式应为：，
故答案为：11，；
（2）解：由题图知，
图①空白部分小正方形的个数是；
图②空白部分小正方形的个数是；
图③空白部分小正方形的个数是；
…，
所以图n空白部分小正方形的个数是：，
故答案为：；
（3）解：由（2）问规律可计算得，

．
19．(1)见解析
(2)2
【分析】（1）等弧所对的圆周角相等，得到，直径，得到，根据等角的余角相等，即可得证；
（2）证明，求出的长，勾股定理求出的长，三角函数，推出，切线得到，解直角三角形，求出的长即可．
【详解】（1）证明：∵，
∴，
∵是的直径，
∴，
∴，
∴；
（2）∵，，
∴，
∴，
∴，
∴（负值舍去）；
∴，
∴，
∴，
∴，
∴，
∵过点作的切线，交的延长线于点，
∴，
∴．
【点睛】本题考查圆周角定理，切线的性质，相似三角形的判定和性质，解直角三角形等知识点，熟练掌握相关知识点，并灵活运用，是解题的关键．
20．
【分析】本题考查了解直角三角形的应用；设交于点，设，根据，入射角，得出，进而求得，根据得出，进而得出；依题意，四边形是矩形，则，进而即可求解．
【详解】解：如图所示，设交于点，

设，
，，，
∴，
，
设，则，
∵，
∴，
∴，
∵，
∴，
设，则，
∴，
∵，
∴，则；
依题意，是矩形，
∴，
∴，
∴．
21．(1)
(2)九年级，理由见解析
(3)
【分析】本题考查求众数和中位数，利用方差判断稳定性，列表法求概率；
（1）根据中位数和众数的确定方法进行求解即可；
（2）求出方差，根据方差判断稳定性即可；
（3）列出表格进行求解即可．
【详解】（1）解：八年级的十个数据排序为：，，，，，，， ，，，
∴；
九年级数据中出现次数最多的是：，
∴；
故答案为：；
（2）九年级学生的测试成绩均为稳定，理由如下：
八年级的方差为：
九年级的方差为：，
∵，
∴九年级学生的测试成绩均为稳定；
（3）由题意，列表如下：
共有12种等可能的结果，其中所选学生中有男生的结果有10种，
∴．
22．(1)
(2)（i）见解析（ii）见解析
【分析】（1）证明，列出比例式进行求解即可；
（2）（i）连接，等边对等角，得到，平行得到，证明，得到，进而得到，推出，即可得出结论；
（ii）连接，证明，得到，三角形的外角和角的和差关系，推出，得到，证明，列出比例式得到，即可得证．
【详解】（1）解：∵矩形矩形，
∴，，
∴，
∴三点共线，
∵，
∴，
∴，
∴，
∴或（舍去）；
（2）（i）连接，
∵，
∴，
∵，
∴，
∵，
∴，
∴，
∴，
∴，即：，
∴；
（ii）连接，
∵，
∴，
∴，
∵，，
∴，
∴，
∵，
∴，
∴，
∴，
∴．
【点睛】本题考查矩形的性质，全等三角形的判定和性质，等腰三角形的判定和性质，旋转的性质，相似三角形的判定和性质，掌握相关知识点，添加辅助线，构造特殊三角形，是解题的关键．
23．(1)
(2)（i）（ii）
【分析】（1）待定系数法求出，的值即可；
（2）（i）对称求出点坐标，求出直线的解析式，联立后，求出点的解析式即可；
（ii）设，求出的解析式，进而求出的坐标，利用，推出，求出的解析式，根据定点的坐标与的值无关，进行求解即可．
【详解】（1）解：∵，
∴，
把代入，得：
，解得：；
（2）（i）由（1）知，
∴，
∴对称轴为直线，
当时，，解得：，
∴，
∵关于直线的对称点为，
∴，
设直线的解析式为，
∴，解得：，
∴，
同法可得，直线的解析式为，
联立，解得：，
∴；
（ii）设，
∵，
设直线的解析式为：，
则：，解得：，
∴，
当时，，
∴，
同法可得：，
∴，
∴，
∴，
设直线的解析式为：，
则：，解得：，
∴
，
，
∴当时，，
∴直线过定点．
【点睛】本题考查二次函数的综合应用，涉及待定系数法求函数解析式，对称性求对称点的坐标，一次函数与坐标轴的交点问题，熟练掌握相关知识点，正确的求出函数解析式，利用数形结合的思想进行求解，是解题的关键，注意计算的准确性．
男1
男2
女1
女2
男1
男1男2
男1女1
男1女2
男2
男2男1
男2女1
男2女2
女1
女1男1
女1男2
女1女2
女2
女2男1
女2男2
女2女1