河南省郑州市郑州中学2023-2024学年八年级下学期期中考试数学试题（含解析）

这是一份河南省郑州市郑州中学2023-2024学年八年级下学期期中考试数学试题（含解析），共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．如图所示图形中，是中心对称图形的是（ ）
A． B． C． D．
2．如图所示的交通标志为一条公路某路段上汽车的最高时速不得超过，若某汽车的时速为，且该汽车没有超速，则下列不等式正确的是（ ）

A．B．C．D．
3．下列式子中，从左到右的变形是因式分解的是（ ）
A．B．
C．D．
4．如果把分式中的和都扩大倍，则分式的值（ ）
A．扩大倍B．扩大倍C．不变D．缩小倍
5．如图，兔子的三个洞口A、B、C构成，猎狗想捕捉兔子，必须到三个洞口的距离都相等，则猎狗应蹲守在的（ ）
A．三条边的垂直平分线的交点B．三条中线的交点
C．三个角的角平分线的交点D．三条高的交点
6．下列命题的逆命题成立的是（ ）
A．如果两个实数的积是正数，那么它们都是正数B．如果两个实数相等，那么它们的平方相等
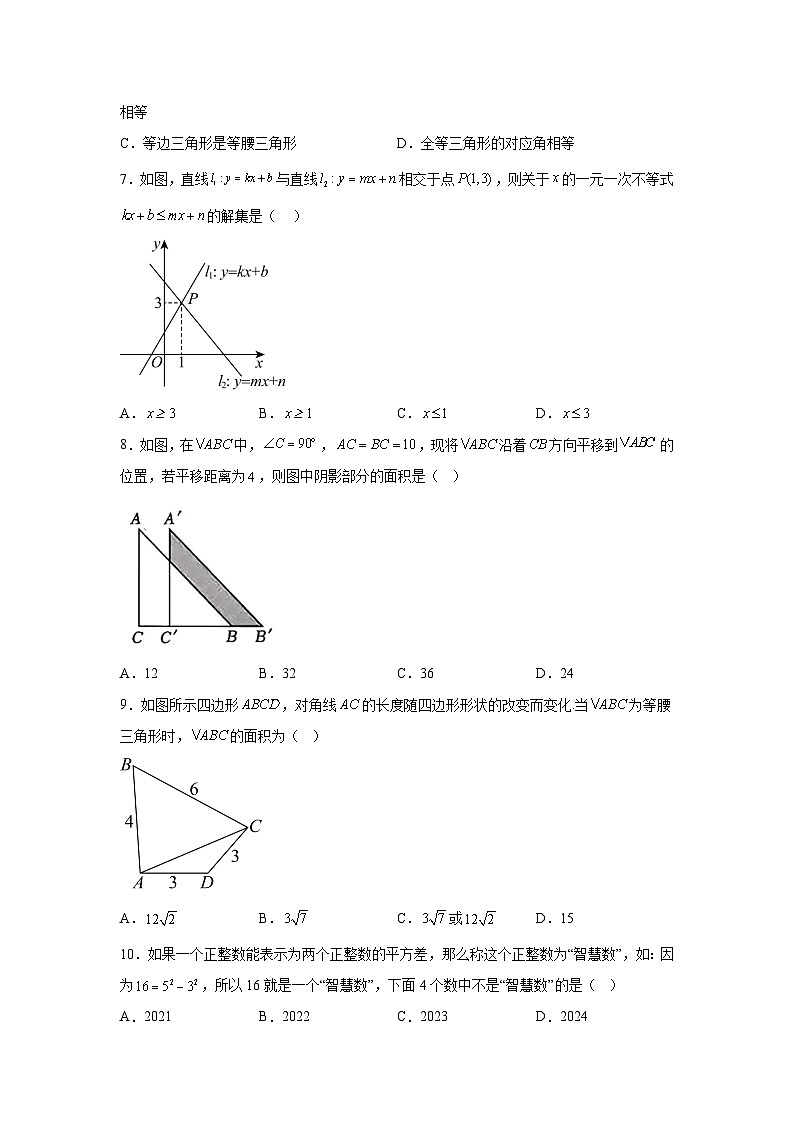
C．等边三角形是等腰三角形D．全等三角形的对应角相等
7．如图，直线与直线相交于点，则关于的一元一次不等式的解集是（ ）
A．B．C．D．
8．如图，在中，，，现将沿着方向平移到的位置，若平移距离为，则图中阴影部分的面积是（ ）
A．12B．32C．36D．24
9．如图所示四边形，对角线的长度随四边形形状的改变而变化.当为等腰三角形时，的面积为（ ）
A．B．C．或D．15
10．如果一个正整数能表示为两个正整数的平方差，那么称这个正整数为“智慧数”，如：因为，所以16就是一个“智慧数”，下面4个数中不是“智慧数”的是（ ）
A．2021B．2022C．2023D．2024
二、填空题（本题共5个小题，每小题3分，共15分）
11．把多项式分解因式的结果是 ．
12．关于x的方程3x+a＝x﹣7的根是正数，则a的取值范围是 ．
13．如图，是中的角平分线，于点E，，，，则长是 ．
14．如图，在中，边的垂直平分线交于点M，交于点P，边的垂直平分线交于点N，交于点Q．若，则的度数为 ．
15．如图，边长为2的正方形绕点逆时针旋转得到正方形，两图叠成一个“蝶形风筝”（如图所示的阴影部分），则这个风筝的面积为 ．
三、解答题（本题共8个小题，共75分）
16．将下列各式分解因式：
(1)；
(2)
17．解不等式组，把解集在数轴上表示出来；并指出它的所有整数解．
18．如图，在平面直角坐标系中，三个顶点的坐标分别为，，．
(1)①若经过平移后得到，已知，画出平移后的；
②可以看作沿的方向一次平移__________个单位长度得到；
(2)将以原点为旋转中心旋转，画出旋转后对应的．
(3)已知点，若点E满足，且，请直接写出E点的坐标__________．
19．如图，是的角平分线，，分别是和的高．，，，，求的长．

20．某大型超市从生产基地购进一批水果，运输过程中质量损失，假设不计超市其它费用
(1)如果超市在进价的基础上提高作为售价，那么请你通过计算说明超市是否亏本；
(2)如果超市至少要获得的利润，请通过计算说明这种水果的售价最低应提高百分之几？
21．阅读理解：
常用的分解因式的方法有提公因式法、公式法，但有很多的多项式只用上述方法就无法分解，如，但我们细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式了，如：
． 这种分解因式的方法叫分组分解法．
解决问题：
(1)分解因式：；
(2)三边满足，判断的形状．
22．综合与实践
问题情境：活动课上，同学们以三角形为背景探究图形变化中的数学问题，如图，中，，，，将从图的位置开始绕点顺时针旋转得到（点，的对应点分别为点，），旋转角为
操作思考：
（1）“实验”小组画出了点恰好落在边上时的图形．连接，如图．试判断的形状，并说明理由：
（2）“求知”小组经过探究发现所在的直线与所在的直线始终垂直，在图中，作直线，于点，请补全图形并证明上述结论；
拓展探究：
（3）“博学”小组继续思考：在整个旋转过程中，若在直线恰好经过的一个顶点，直接写出此时的长度为
1．C
【分析】本考查了中心对称图形的概念．把一个图形绕某一点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．根据中心对称图形的概念求解．
【详解】解：A、不是中心对称图形，不符合题意；
B、不是中心对称图形，不符合题意；
C、是中心对称图形，符合题意；
D、不是中心对称图形，不符合题意．
故选：C．
2．D
【分析】根据题意直接列不等式即可作答．
【详解】根据题意，有：，
故选：D．
【点睛】本题考查了列不等式的知识，明确题意是解答本题的关键．
3．C
【分析】根据分解因式的定义逐个判断即可．
【详解】解：A．无法分解因式，故本选项不符合题意；
B．计算错误，故本选项不符合题意；
C．，属于分解因式，故本选项符合题意；
D．，等式由左到右的变形不属于分解因式，故本选项不符合题意；
故选：C．
【点睛】本题考查了因式分解的定义，注意：把一元多项式化成几个整式的积的形式，叫因式分解，也叫分解因式．
4．B
【分析】根据分式的基本性质即可求出答案；
【详解】解：
故选：B．
【点睛】本题考查了分式的基本性质；解题的关键是熟练运用分式的基本性质进行化简比较．
5．A
【分析】此题考查了线段垂直平分线的性质，以及三角形的角平分线、中线和高，熟练掌握性质是解本题的关键．用线段垂直平分线性质判断即可．
【详解】解：猎狗到三个顶点的距离相等，则猎狗应蹲守在的三条边垂直平分线的交点．
故选：A
6．A
【分析】本题主要考查逆命题的判定，首先写出各个命题的逆命题，再进一步判断真假即可．
【详解】解：A．逆命题是如果两个数都是正数，那么它们的积是正数，真命题，符合题意；
B．逆命题是如果两个实数的平方相等，那么这两个实数相等，假命题，不符合题意；
C．逆命题是等腰三角形是等边三角形，假命题，不符合题意；
D．逆命题是如果两个三角形的三组对应角相等，那么这两个三角形全等，假命题，不符合题意；
故选：A．
7．C
【分析】本题考查了一次函数与一元一次不等式，解题关键是结合图像进行解答．结合函数图像，写出直线在直线下方所对应的自变量的范围即可．
【详解】解：∵直线与直线相交于点，
∴由图像可知，关于的一元一次不等式的解集为．
故选：C．
8．B
【分析】因为平移后的三角形和面积不变，两个三角形有重叠的公共部分为三角形，所以阴影部分的面积和梯形的面积相等．本题的关键是利用平移的性质得出小三角形的底和高．
【详解】解： 如图：
∵现将沿着方向平移到的位置， ，
∴
∴
∵若平移距离为4，
∴
∴阴影部分的面积和梯形的面积相等
∴阴影面积．
故选：B．
9．B
【分析】本题考查了勾股定理，关键是注意分类讨论．分、两种情况讨论即可求解．
【详解】解：当时，
过作，交于点，
，，
，
由勾股定理，，
，
当时，
不满足小于，
此种情况不存在，
故选：B
10．B
【分析】本题考查了平方差公式分解因式的应用，牢记是解题的关键．设k是正整数，证明除1外，所有的奇数都是智慧数；除4外，所有的能被4整除的偶数都是智慧数，即可得答案．
【详解】解：设k是正整数，
∵，
∴除1外，所有的奇数都是智慧数，所以，A，C选项都是智慧数，不符合题意；
∵，
∴除4外，所有的能被4整除的偶数都是智慧数，所以D选项是智慧数，不符合题意，
B选项2022不是奇数也不是4的倍数，不是智慧数，符合题意．
故选：B．
11．
【分析】直接利用平方差公式分解因式得出答案．
【详解】解：=．
故答案为．
【点睛】此题主要考查了公式法因式分解，正确应用公式是解题关键．
12．a＜﹣7
【分析】求出方程的解，根据方程的解是正数得出>0，求出即可．
【详解】解：3x+a=x-7
3x-x=-a-7
2x=-a-7
x=，
∵＞0，
∴a＜-7，
故答案为a＜-7
【点睛】本题考查解一元一次不等式和一元一次方程的应用，关键是求出方程的解进而得出不等式．
13．6
【分析】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．作于F，根据角平分线性质定理得到，再利用三角形面积公式求解即可．
【详解】解：作于F，如图，
∵是中的角平分线，，，
∴，
∵，
∴，
∴．
故答案为6．
14．##108度
【分析】本题考查了线段垂直平分线的性质，等腰三角形的性质，以及三角形内角和定理，熟练掌握轴对称的性质是解答本题关键．由线段垂直平分线的性质得，从而，由三角形内角和求出即可求解．
【详解】解：∵是的垂直平分线，是的垂直平分线，
∴，
∴，
∵，
∴，
∴，
∴．
故答案为：．
15．
【分析】本题考查正方形的性质，勾股定理的应用，化为最简二次根式，旋转的性质，四边形面积计算等知识，用两个正方形面积和减去重叠部分面积即可，重叠部分可看作两个全等的直角三角形．
【详解】解：设交于点，连接，

∵，，，
∴，
∴，
旋转角，
，
，
∴，
在中，，
∴，
，
．
故答案为：．
16．(1)
(2)
【分析】本题考查了因式分解，熟练掌握知识点是解题的关键．
（1）利用完全平方公式进行因式分解即可；
（2）先提取公因式，再用平方差公式进行分解即可．
【详解】（1）解：；
（2）解：.
17．，所有整数解为3，4，5，数轴见解析
【分析】本题考查的是解一元一次不等式组．先求出两个不等式的解集，再求其公共解集，然后确定这个范围内的整数解即可．
【详解】解：解不等式①，得，
解不等式②，得：，
该不等式组的解集为，
其解集在数轴上表示如图所示，
它的所有整数解为3，4，5．
18．(1)①见解析；②；
(2)见解析
(3)或
【分析】本题主要考查了坐标与图形变化—平移和中心对称，坐标与图形，勾股定理：
（1）①根据点A和点的坐标可得平移方式为向右平移4个单位长度，向上平移1个单位长度，据此求出B、C对应点的坐标，再顺次连接对应点即可得到答案；②利用勾股定理求出得长即可得到答案；
（2）根据关于原点对称的点横纵坐标都互为相反数得到A、B、C对应点的坐标，进而顺流连接对应点即可得到答案；
（3）根据B、D坐标得到轴，且，据此可得答案．
【详解】（1）解：①如图所示，即为所求；
②∵，，
∴，
∴可以看作沿的方向一次平移个单位长度得到，
故答案为：；
（2）解：如图所示，即为所求；
（3）解：∵，，
∴轴，
∵，
∴轴，且，
∵，
∴点D的坐标为或，
故答案为：或．
19．
【分析】本题考查角平分线的定义及线段垂直平分线的性质，含30度角的直角三角形的性质．证明，可得出垂直平分．利用面积法可求出的长，再根据即可解决问题．
【详解】解：平分，
．
分别是和的高，
．
在和中，
，
，
，
点和点在的垂直平分线上，
垂直平分．
，，
，
又，
．
，平分，
．
在中，
在中，
．
20．(1)超市亏本
(2)这种水果的售价最低应提高
【分析】考查了一元一次不等式的应用， 解题的关键是：
（1）假设超市购进这批水果的总量为千克，每千克进价为元，表示出超市最终的销售额，然后总进价比较即可；
（2）设这种水果的售价最低应提高，根据关系式：总售价-总进价进价进行计算即可．
【详解】（1）解：假设超市购进这批水果的总量为千克，每千克进价为元，
超市最终的销售额为（元）．
，
这一次销售中，超市亏本．
（2）解：假设超市购进这批水果的总量为千克，每千克进价为元，
设这种水果的售价最低应提高，
依题意，得：，
解得：．
答：这种水果的售价最低应提高．
21．(1)
(2)等腰三角形
【分析】本题考查分组分解法分解因式，因式分解的应用，等腰三角形的定义．
（1）先将三项分一个组，运用完全正确平方公式分解，再运用平方差公式分解即可；
（2）先运用因式分解，将等式变形为，从而得出，再根据等腰三角形的定义，即可求解．
【详解】（1）解：
；
（2）的形状为等腰三角形．
理由：，
．
，
，
是三边长
．
．
的形状为等腰三角形．
22．（1）等边三角形，理由见解析（2）见解析（3）或
【分析】本题主要考查了旋转的性质、等腰三角形的判定与性质、等边三角形的判定与性质、含30度角的直角三角形的性质、勾股定理等知识，理解并掌握旋转的性质是解题关键．
（1）首先证明为等边三角形，易得，进而可得，结合即可证明结论．
（2）根据题意作出图形；设与交于点，结合旋转的性质可得，，再证明，进而可得，，因为，所以，即可证明即；
（3）分直线经过点和直线经过点两种情况，分别求解即可．
【详解】解：（1）是等边三角形
由旋转得：，，，
在中，，
是等边三角形，
，
，
，
是等边三角形．
（2）由旋转可知，，，，
∴，
作直线，于点，设与交于点，如图所示：
在中，，
在中，，
∵，
∴，
即．
（3）∵，，，
∴，，
∴，
由旋转的性质可得，，，，，，
分两种情况讨论：
如下图，当直线经过点时，过点作，交延长线于点，
∵，，
∴为等边三角形，
∴，，
∴，
∵，
∴，
∴，
∴，，
∴在中，；
如下图，当直线经过点时，
∵，
∴，
∴，
∴，
∴．
综上所述，的的长度为或．
故答案为：或．