2024 浙江省 温州市 中考 数学 模拟 练习 试卷（解析版）

这是一份2024 浙江省 温州市 中考 数学 模拟 练习 试卷（解析版），文件包含2024浙江省温州市中考数学模拟练习试卷解析版doc、2024浙江省温州市中考数学模拟练习试卷doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
1．2024的倒数是（ ）
A．B．2024C．D．
【答案】A
【分析】本题主要考查了倒数，解题的关键是熟练掌握倒数的定义，“乘积为1的两个数互为倒数”．
【详解】解：2024的倒数．
故选：A．
2. 直六棱柱如图所示，它的俯视图是（ ）

A．B．C． D．
【答案】C
【分析】直接从上往下看，得到的是一个六边形，即可选出正确选项．
【详解】解:从上往下看直六棱柱，看到的是个六边形；
故选：C．
在2023年春节假期，全国国内旅游出游超过308000000人次．
数据308000000用科学记数法表示为（ ）
A．B．C．D．
【答案】C
【分析】308000000用科学记数法表示成的形式，其中，，代入可得结果．
【详解】解：308000000的绝对值大于表示成的形式，
∵，，
∴308000000表示成，
故选C．
4 . 如图是某校七年级学生参加课外兴趣小组的扇形统计图（每人只参加一项），
若参加书法兴趣小组的人数是30人，则参加绘画兴趣小组的人数是（ ）
A．36人B．40人C．60人D．200人
【答案】C
【分析】先求出参加书法兴趣小组的人数所占的百分比，可求出总人数，
再用总人数乘以参加绘画兴趣小组的人数所占的百分比，即可求解．
【详解】解：根据题意得：参加书法兴趣小组的人数所占的百分比为，
∴总人数为人，
∴参加绘画兴趣小组的人数是人．
故选：C
5. 下列运算正确的是（ ）
A．B．
C．D．
【答案】C
【分析】根据合并同类项、单项式除法、积的乘方、单项式乘法的运算法则逐项计算判断即可．
【详解】A.3a与2b不是同类项，不能合并，故本选项错误；
B.，故本选项错误；
C.，故本选项正确；
D.，故本选项错误．
故选：C．
6 .在践行“安全在我心中，你我一起行动”主题手抄报评比活动中，
共设置“交通安全、消防安全、饮食安全、防疫安全”四个主题内容，推荐两名学生参加评比，
若他们每人从以上四个主题内容中随机选取一个，则两人恰好选中同一主题的概率是（ ）
A．B．C．D．
【答案】D
【分析】设“交通安全、消防安全、饮食安全、防疫安全”四个主题内容分别为A、B、C、D，画出树状图进行求解即可．
【详解】解：设“交通安全、消防安全、饮食安全、防疫安全”四个主题内容分别为A、B、C、D，画树状图如下：
共有16种等可能的结果，两人恰好选中同一主题的结果有4种，
则两人恰好选中同一主题的概率为．
故选：D．
7.一次函数中，随的增大而增大，且，则此函数的图象大致为（ ）
A．B．C．D．
【答案】D
【分析】先根据一次函数的增减性可得，再根据可得，由此即可得出答案．
【详解】解：一次函数中，随着的增大而增大，
，且可排除选项A和B，
又，
，
函数图象与轴的交点在轴下方，
故选：D．
小亮的妈妈用30元买了甲、乙两种水果，甲种水果每千克3元，乙种水果每千克5元，
且乙种水果比甲种水果少买了2kg．小亮妈妈两种水果各买了多少千克？
设小亮妈妈买了甲种水果xkg，乙种水果y kg，则可列方程组为（ ）
A．B．C．D．
【答案】B
如图，四边形内接于，，．
若，，则的度数与的长分别为（ ）

A. 10°，1B. 10°，C. 15°，1D. 15°，
【答案】C
【解析】
【分析】过点O作于点E，由题意易得，然后可得，，，进而可得，最后问题可求解．
【详解】解：过点O作于点E，如图所示：

∵，
∴，
∵，
∴，
∵，
∴，
∴，
∵，，，
∴，，，
∴，，，
∴，
∴，
∴；
故选C．
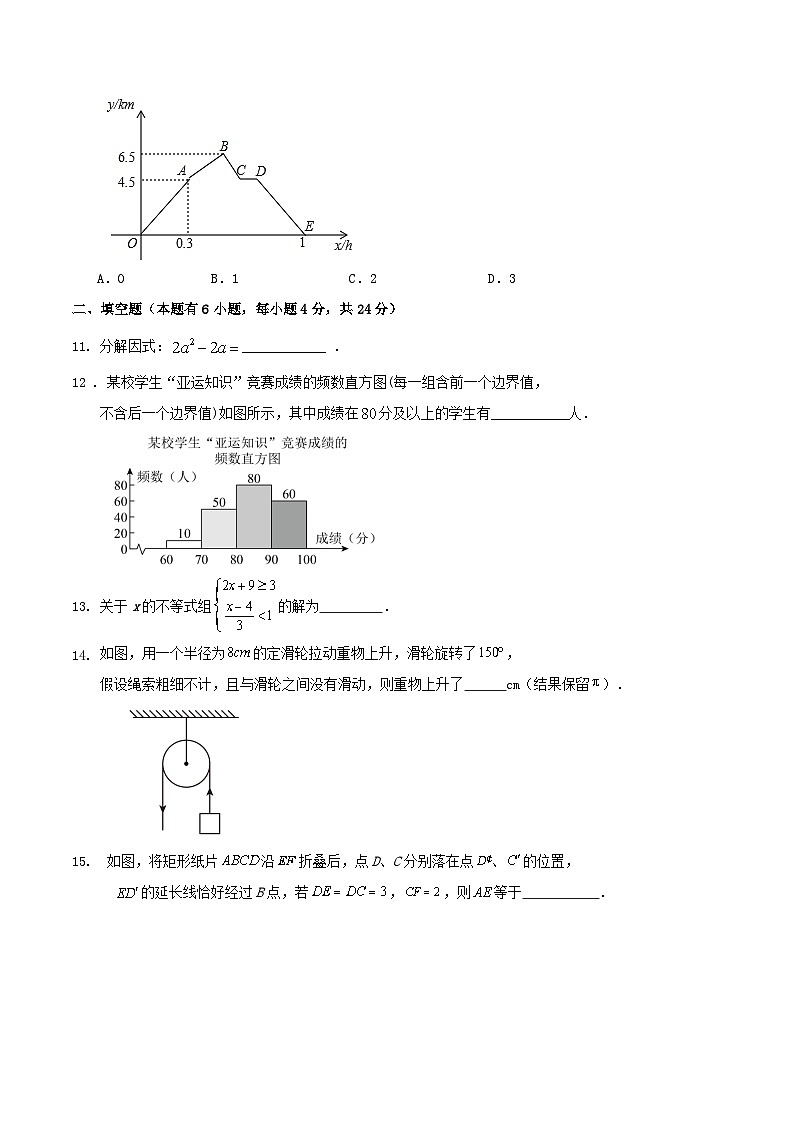
从甲地到乙地，先是一段平路，然后是一段上坡路，小明骑车从甲地出发，到达乙地后立即返回甲地，
途中休息了一段时间，假设小明骑车在平路、上坡、下坡时分别保持匀速前进，
已知小明骑车上坡的速度比在平路上的速度每小时少5km，
下坡的速度比在平路上的速度每小时多5km．设小明出发xh后，到达离甲地ykm的地方，
图中的折线OABCDE表示y与x之间的函数关系．
①小明骑车在平路上的速度为15km/h
②小明途中休息了0.1h；
③小明从甲地去乙地来回过程中，两次经过距离甲地5.5km的地方的时间间隔为0.15h
则以上说法中正确的个数为（ ）

A．0B．1C．2D．3
【答案】D
【分析】①由函数图象可知平路路段的路程为4.5千米，行驶的时间为0.3小时，从而可求得行驶的速度；
②由速度＝路程÷时间就可以求出小明在平路上的速度，就可以求出返回的时间，进而得出途中休息的时间；
③两次的时间间隔就是：去乙地时距离甲地5.5千米剩下的路程的时间加上返回时到达距离甲地5.5km时用的时间，根据路程和速度算出时间即可．
【详解】解：①小明骑车在平路上的速度为：4.5÷0.3＝15（km/h），故①正确；
②小明骑车在上坡路的速度为：15﹣5＝10（km/h），
小明骑车在下坡路的速度为：15+5＝20（km/h）．
∴小明在AB段上坡的时间为：（6.5﹣4.5）÷10＝0.2（h），
BC段下坡的时间为：（6.5﹣4.5）÷20＝0.1（h），
DE段平路的时间和OA段平路的时间相等为0.3h，
∴小明途中休息的时间为：1﹣0.3﹣0.2﹣0.1﹣0.3＝0.1（h），故②正确；
③小明第一次经过距离甲地5.5km的地方时是上坡，其距离乙地还需骑车：（6.5﹣5.5）÷10＝0.1h，
小明第二次经过距离甲地5.5km的地方时是下坡：（6.5﹣5.5）÷20＝0.05h，
则两次的时间间隔是：0.1+0.05＝0.15h，故③正确；
综上所述：①②③都正确；
故选D．
二、填空题（本题有6小题，每小题4分，共24分）
11. 分解因式：____________ ．
【答案】
【解析】
【分析】利用提公因式法进行解题，即可得到答案．
【详解】解：．
故答案为：．
12 . 某校学生“亚运知识”竞赛成绩的频数直方图(每一组含前一个边界值，
不含后一个边界值)如图所示，其中成绩在分及以上的学生有___________人．

【答案】
【解析】
【分析】根据频数直方图，直接可得结论．
【详解】解：依题意，其中成绩在分及以上的学生有人，
故答案为：．
13. 关于x的不等式组的解为 ．
【答案】
【分析】分别求出每一个不等式的解集，根据口诀：
同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集即可．
【详解】解：
解不等式①得，
解不等式②得，
所以，不等式组的解集为：
故答案为：
如图，用一个半径为的定滑轮拉动重物上升，滑轮旋转了，
假设绳索粗细不计，且与滑轮之间没有滑动，则重物上升了 cm（结果保留）．

【答案】
【分析】根据弧长的计算方法计算半径为，圆心角为的弧长即可．
【详解】解：由题意得，重物上升的距离是半径为，圆心角为所对应的弧长，
即，
故答案为：．
15. 如图，将矩形纸片沿折叠后，点D、C分别落在点、的位置，
的延长线恰好经过B点，若，，则等于 ．

【答案】4
【分析】根据矩形及折叠的性质可知，，，则，设，则，，利用勾股定理可得：，即：，求出即可求得的长度．
【详解】解：∵四边形是矩形，，
∴，，，
∴，
由折叠可知，，，
∴，
∴，
设，则，，
则由勾股定理可得：，即：，
解得：，
则，
故答案为：4．
如图，在中，为坐标原点，，，
点，都在反比例函数的图象上．
若点横坐标为1，则的值为_______

【答案】
【分析】作轴，轴，且线段和线段的延长线交于点M．根据题意易证，又可用k表示出A点坐标．从而即可求出用k表示的B点坐标，代入反比例函数解析式，解出k即可．
【详解】如图，作轴，轴，且线段和线段的延长线交于点M．
∵，，
∴，
∴在和中，
∴．
根据题意可知A点坐标为，
∴，，
∴B点坐标为，
又∵点B在该函数图象上，
∴，
解得：．
经检验都是原方程的根．
∵函数图象在第一象限，即，
∴舍去，
故．
故答案为．
三、解答题（本题有8小题，共66分．解答需写出必要的文字说明、演算步骤或证明过程）
17. 计算：
(1)
(2)．
【答案】(1)
(2)
【分析】（1）根据负指数幂、绝对值化简及特殊角三角函数直接求解即可得到答案；
（2）先通分化简括号里的分式，再约分化简，化到最简即可得到答案；
【详解】（1）解：原式
；
（2）解：原式
；
如图，在的方格纸中，每个小方格的边长为1．
已知格点P，请按要求画格点三角形（顶点均在格点上）．

在图中画一个等腰三角形，使底边长为，点E在上，点F在上，
再画出该三角形绕矩形的中心旋转180°后的图形．
在图中画一个，使，点Q在上，点R在上，
再画出该三角形向右平移1个单位后的图形．
【答案】（1）见解析 （2）见解析
【解析】
【分析】（1）底边长为即底边为小方格的对角线，根据要求画出底边，再在其底边的垂直平分线找到在格点上的顶点即可得到等腰，然后根据中心旋转性质作出绕矩形的中心旋转180°后的图形．
（2）根据网格特点，按要求构造等腰直角三角形，然后按平移的规律作出平移后图形即可．
【小问1详解】
（1）画法不唯一，如图1（ ，），或图2（）．

【小问2详解】
画法不唯一，如图3或图4．

19 .随着春天气温变暖，某校组织同学们分别到A，B，C，D四个景点进行春游活动，
学校把学生前往四个地方的人数做了统计，得到下列两幅不完整的统计图，如图所示．

本次参加春游活动学生总人数有 人，
在扇形统计图中，去D景点活动的人数对应扇形的圆心角的度数是 度．
请你将条形统计图补充完整．
本次春游活动中，学校分配给九年级学生甲、乙、丙三辆车，
小明与小华都可以从这三辆车中任选一辆搭乘．求小明与小华同车的概率（要求画树状图或列表）．
【答案】(1)，
(2)补图见解析
(3)列表见解析，
【分析】（1）根据，计算求解本次参加春游活动学生总人数；根据，计算求解D景点活动的人数对应扇形的圆心角的度数即可；
（2）由题意知，D景点活动的人数为（人），然后补全统计图即可；
（3）根据题意列表，然后求概率即可．
【详解】（1）解：由题意知，本次参加春游活动学生总人数有（人），
D景点活动的人数对应扇形的圆心角的度数为，
故答案为：400，108；
（2）解：由题意知，D景点活动的人数为（人），补图如下：
（3）解：根据题意列表如下：
由表可知，小明与小华共有9种等可能的选择情况，其中小明与小华同车共有3种等可能的情况，
∴小明与小华同车的概率为，
∴小明与小华同车的概率为．
20. 如图，直线与双曲线相交于，B两点，与x轴相交于点．

分别求一次函数与反比例函数的解析式；
(2) 连接，则的面积__________；
【答案】(1)，
(2)
【分析】将已知点坐标代入函数表达式，即可求解;
两函数解析式联立成方程组，求出点B的坐标，然后根据即可以解决问题；
根据图象即可解决问题.
【详解】（1）将代入,
得
解得：，
∴一次函数的解析式为，
将代入
得,
∴反比例的解析式为
（2）∵直线的解析式为与轴交点,
∴点的坐标为,
由 解得 或，
∴点的坐标为,
∴
如图，在中，，D是上一点，，
过点D作于点F，过点C作交的延长线于点E．

求证：四边形是平行四边形．
(2 若，，求的长．
【答案】(1)见解析
(2)9
【分析】（1）根据垂直的定义可得，再结合即可证明四边形BDCE是平行四边形；
（2）根据平行线的性质可得，再根据平行四边形的性质可得，运用正弦的定义可得，由勾股定理可得；设、则、，然后根据勾股定理列方程求得x即可解答．
【详解】（1）解：∵，
∴，
∵，
∴，
∴
∵，
∴四边形BDCE是平行四边形．
（2）解：∵，
∴，
∵四边形是平行四边形，
∴
∵，
∴，
∴,
∴,
设，则，，
∴,即，
∴，即．
22. 如图，已知抛物线的顶点为A，与x轴的一个交点为，与y轴的交点为C．

(1)求m的值，并确定抛物线的顶点A的坐标．
(2)在抛物线上有一点P，使得的面积是3，求点P的坐标．
【答案】(1)；；
(2)或．
【分析】（1）把点B坐标代入二次函数解析式即可求出m的值，然后利用配方法求出顶点的坐标；
（2）先设点，然后根据的面积是3，列式求解即可得出答案．
【详解】（1）解：抛物线与x轴的一个交点为，
，
，
，
，
故m的值为，抛物线的顶点A的坐标；
（2）解：当时，，
，
，
点P在抛物线上，设点，
的面积是3，
，
，
当时，，即；
当时，，即；
故点P的坐标为：或．
如图，一艘游轮在处测得北偏东的方向上有一灯塔B，
游轮以海里/时的速度向正东方向航行2小时到达处，
此时测得灯塔在处北偏东的方向上．

(1)求到直线的距离；
(2)求游轮继续向正东方向航行过程中与灯塔的最小距离是多少海里？
（结果精确到1海里，参考数据：，，，，）
【答案】(1)40海里
(2)77海里
【分析】（1）过点C作于点E，在中，，
证得是等腰三角形，根据等腰三角形的性质即可解得；
（2）由题意可得，，求出，
作于点F，在中，根据即可解得．
【详解】（1）如图，由题意可得，，
过点C作于点E，
在中，，
∴是等腰直角三角形，
由题意得： ，
∴，
即点C到线段的距离为40海里；
（2）由题意可得，，
则，
∵，
∴，
∵在中，
，
∴，
∴
作于点F，
在中，
∴
答：与灯塔B的最小距离是77海里．
（1）如图1，在正方形ABCD中，点E，F分别是AB，AD上的两点，
连接DE，CF，DE⊥CF，则的值为____；

（2）如图2，在矩形ABCD中，AD=5，CD=3，点E是AD上的一点，
连接CE，BD，且CE⊥BD，则的值为______；

如图3，在四边形ABCD中，∠A=∠B=90°，点E为AB上一点，
连接DE，过点C作DE的垂线交ED的延长线于点G，交AD的延长线于点F，求证：；

如图4，在Rt△ABD中，∠BAD=90°，AB=3，AD=9，将△ABD沿BD翻折，
点A落在点C处得△CBD，点E，F分别在边AB，AD上，连接DE，CF，DE⊥CF．
请问是定值吗?若是，直接写出这个定值，若不是，请说明理由．

【答案】（1）1；（2）；（3）见解析；（4）是定值，且这个定值为．
【分析】（1）证明△AED≌△DFC，根据全等三角形的性质得到DE＝CF，得到答案；
（2）证明△DEC∽△ABD，根据相似三角形的性质计算即可；
（3）过点C作CH⊥AF交AF的延长线于点H，证明△DEA∽△CFH，列出比例式，证明结论；
（4）连接AC交BD于H，CF与DE交于G，CF与DB交于P，证明△ACF∽△BDE，根据勾股定理算出BD的长，根据直角三角形ABD的面积算出AH的长，可以得出AC的长，计算即可．
【详解】解：（1）∵四边形ABCD为正方形，
∴AD=DC，∠A=∠FDC=90°，
∵DE⊥CF，
∴∠ADE+∠DFC=90°，∠DFC+∠DCF=90°，
∴∠ADE=∠DCF，
在△ADE和△DCF中，
，
∴△ADE≌△DCF（ASA），
∴DE=CF，
∴，
故答案为1．
（2）∵四边形ABCD为矩形，
∴∠A=∠EDC=90°，
∵CE⊥BD，
∴∠ADB+∠CED=90°，∠CED+∠DCE=90°，
∴∠ADB=∠DCE，
∴△ADB∽△DCE，
∴，
故答案为：．
（3）过点C作CH⊥AD，交AD延长线于H，如图所示：
∵∠H=∠A=∠B=90°，
∴四边形ABCH为矩形，
∴CH=AB，
∵CG⊥EG，
∴∠G=90°=∠A=∠H，
∵∠ADE=∠GDF，
∴△ADE∽△GDF，
∵∠GFD=∠HFC，
∴△GDF∽△HCF，
∴△ADE∽△HCF，
∴．
（4）是定值；理由如下：
连接AC交BD于H，CF与DE交于G，CF与DB交于P，如图所示：
∵将△ABD沿BD翻折，点A落在点C处，得到△CBD，
∴AC⊥BD，
∴∠BAH+∠CAF=90°，∠BAH+∠EBD=90°，∠CHP=90°，
∴∠CAF=∠DBE，
∵CF⊥DE，
∴∠PGD=90°=∠CHP，
∵∠HPC=∠GPD，
∴∠ACF=∠BDE，
∴△ACF ∽△BDE，
，
∵AB=3，AD=9，
根据勾股定理，
，
，
．
甲
乙
丙
甲
（甲，甲）
（甲，乙）
（甲，丙）
乙
（乙，甲）
（乙，乙）
（乙，丙）
丙
（丙，甲）
（丙，乙）
（丙，丙）