2024年浙江省嘉兴市中考数学模拟练习试卷（解析卷）

这是一份2024年浙江省嘉兴市中考数学模拟练习试卷（解析卷），文件包含2024年浙江省嘉兴市中考数学模拟练习试卷解析卷doc、2024年浙江省嘉兴市中考数学模拟练习试卷doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
第I卷（选择题共30分）
一、选择题（本题有10小题，每小题3分，共30分．）
1．计算的结果是（ ）
A．B．C．2D．
【答案】A
【分析】根据有理数的乘法法则进行计算，有理数乘法法则即两数相乘，同号得正，异号得负，并把绝对值相乘．
【详解】．
故选A
2．由四个相同的小正方体搭成的几何体如图所示，它的俯视图是（ ）
A．B．C．D．
【答案】D
【分析】根据俯视图的意义画图即可．
【详解】 俯视图是，
故选D．
3．下列问题中，采用的调查方式合适的是（ ）
A．了解一批袋装食品是否含有防腐剂，采用普查方式
B．调查鞋厂生产的鞋底能承受的弯折次数，采用普查方式
C．了解某班学生“跑”的成绩，采用抽样调查方式
D．了解中央电视台新闻联播的收视率，采用抽样调查方式
【答案】D
【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似即可解答．
【详解】解：对于A，了解一批袋装食品是否含有防腐剂，采用抽样调查方式较为合适，故A选项不符题意；
对于B，调查鞋厂生产的鞋底能承受的弯折次数，采用抽样调查方式较为合适，故B选项不符题意；
对于C，了解某班学生“跑”的成绩，采用普查方式较为合适，故C选项不符题意；
对于D，了解中央电视台新闻联播的收视率，采用抽样调查方式较为合适，故D选项符合题意；
故选：D．
4．下列计算正确的是（ ）
A．B．
C．D．
【答案】B
【分析】运用幂的乘除运算法则可判断A、B选项，运用完全平方公式可判断C选项，运用同类项合并可判断D选项，即可选出答案．
【详解】解：A．，故选项错误，不符合题意；
B．，故选项正确，符合题意；
C．，故选项错误，不符合题意；
D．，故选项错误，不符合题意；
故选：B．
5 . 实数，在数轴上对应点的位置如图所示，则下列结论正确的是（ ）

A．B．
C．D．
【答案】D
【分析】根据题意可得，然后根据数的乘法和加法法则以及不等式的性质进行判断即可.
【详解】解：由题意可得：，所以，
∴，
观察四个选项可知：只有选项D的结论是正确的；
故选：D.
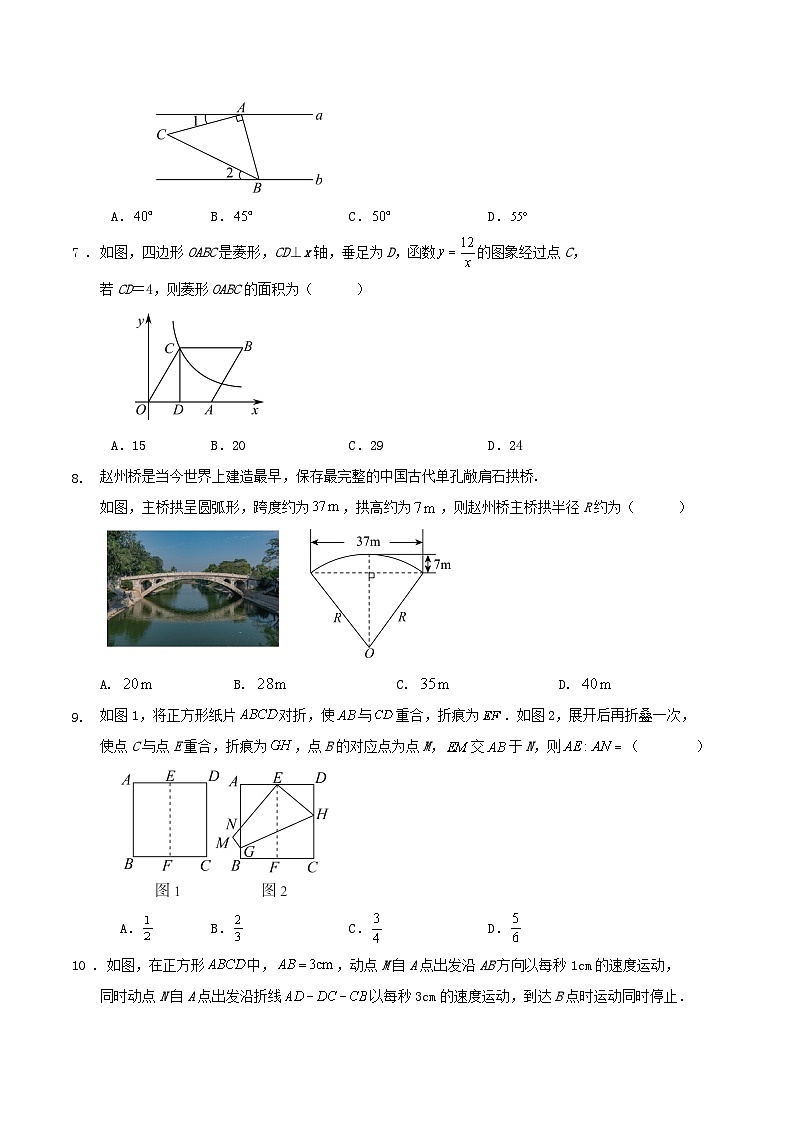
6. 如图，直线，的直角顶点A落在直线上，点B落在直线上，
若，，则的大小为（ ）

A．B．C．D．
【答案】C
【分析】根据两直线平行，同旁内角互补，进行求解即可.
【详解】解：∵，
∴，
∵，，，
∴.
故选：C
7 .如图，四边形OABC是菱形，CD⊥x轴，垂足为D，函数的图象经过点C，
若CD＝4，则菱形OABC的面积为（ ）

A．15B．20C．29D．24
【答案】B
【分析】根据反比例函数系数k的几何意义得到S△COD＝×12＝6，得到OD＝3，根据勾股定理得到OC＝＝5，根据菱形的性质得到OC＝OA＝5，则可求解菱形OABC的面积．
【详解】解：∵函数的图象经过点C，CD⊥x轴，
∴S△COD＝×12＝6．
∵CD＝4，
∴OD＝3．
∴由勾股定理得OC＝＝5．
∵四边形OABC是菱形，
∴OC＝OA＝5．
∴S菱形OABC＝OA•CD＝5×4＝20．
故选：B．
赵州桥是当今世界上建造最早，保存最完整的中国古代单孔敞肩石拱桥.
如图，主桥拱呈圆弧形，跨度约为，拱高约为，则赵州桥主桥拱半径R约为（ ）

A. B. C. D.
【答案】B
【解析】
【分析】由题意可知，，，主桥拱半径R，根据垂径定理，得到，
再利用勾股定理列方程求解，即可得到答案．
【详解】解：如图，

由题意可知，，，主桥拱半径R，
，
是半径，且，
，
在中，，
，
解得：，
故选B
如图1，将正方形纸片对折，使与重合，折痕为．如图2，展开后再折叠一次，
使点C与点E重合，折痕为，点B的对应点为点M，交于N，则（ ）

A．B．C．D．
【答案】C
【分析】设正方形的边长为，，表示出，再根据翻折变换的性质表示出、，然后利用勾股定理列出方程求出，再根据同角的余角相等求出，然后根据锐角的正切值等于对边比邻边列式计算即可得解．
【详解】解：设正方形的边长为，，
则，
由翻折的性质，可得：，
．
在中，，
即，
解得：．
∵，
∴．
∵，
∴，
∴，
∴．
故选：C
10 . 如图，在正方形中，，动点M自A点出发沿AB方向以每秒1cm的速度运动，
同时动点N自A点出发沿折线以每秒3cm的速度运动，到达B点时运动同时停止．
设的面积为y（cm2）．运动时间为x（秒），
则下列图象中能大致反映y与x之间函数关系的是（ ）

A． B． C． D．
【答案】B
【分析】根据题意，分三段（，，）分别求解与的解析式，从而求解．
【详解】解：当时，分别在线段，

此时，
，为二次函数，图象为开口向上的抛物线；
当时，分别在线段，
此时，底边上的高为，
，为一次函数，图象为直线；
当时，分别在线段，
此时，底边上的高为，
，为二次函数，图象为开口向下的抛物线；
结合选项，只有B选项符合题意，
故选：B
第Ⅱ卷（非选择题 共90分）
二、填空题（本题有6小题，每小题4分，共24分）
11．若，则 ．
【答案】7或
【分析】根据绝对值的性质即可作答．
【详解】解：∵，
∴或
故答案为：7或
12．如图，已知△ABC中，点D在AB上，点E在AC上，DE∥BC．AD＝2，DB＝3，AE＝4，则EC＝ ；
【答案】6
【分析】根据平行线分线段成比例定理得到，于是得到答案．
【详解】解：∵DE∥BC，
∴，
∴，
∴EC=6，
故答案为：6．
13．连续投掷两枚质地均匀的硬币，两枚硬币恰好是一正一反的概率是
【答案】/0.5
【分析】本题考查列表法或树状图求概率、概率公式；画树状图可得共有4种等可能的结果，其中两枚硬币恰好是一正一反有2种等可能的结果，再利用概率公式求解即可．
【详解】解：画树状图如下：
共有4种等可能的结果，其中两枚硬币恰好是一正一反有2种等可能的结果，
∴两枚硬币恰好是一正一反的概率是，
故答案为：．
14． 2024年元旦期间，小华和家人到汾河公园景区游玩，湖边有大小两种游船，小华发现：
2艘大船与3艘小船一次共可以满载游客人，1艘大船与1艘小船一次共可以满载游客人．
则1艘大船可以满载游客的人数为 ．

【答案】人
【分析】设1艘大船可以满载游客x人，1艘小船可以满载游客y人，由题意：2艘大船与3艘小船一次共可以满载游客人，1艘大船与1艘小船一次共可以满载游客人．列出二元一次方程组，解方程组即可．
【详解】解：设1艘大船可以满载游客x人，1艘小船可以满载游客y人，
依题意得：，
解得：，
即1艘大船可以满载游客的人数为人，
故答案为：人．
15．如图，正五边形的边长为，以为圆心，以为半径作弧，则阴影部分的面积为 （结果保留）．

【答案】
【分析】根据正多边形内角和公式求出正五边形的内角和，再求出的度数，利用扇形面积公式计算即可．
【详解】解：正五边形的内角和，
，
，
故答案为：．
16．如图，在正方形中，为的中点，为的中点，的延长线与的延长线交于点，与相交于点．若，则的长为 ．

【答案】
【分析】根据正方形的性质可求出，，则有点为的中点，是的中线，再证，根据三角形相似的性质可求出的长，由此即可求解．
【详解】解：∵正方形中，为的中点，为的中点，
∴，，，
∴，
∴，
∵，
∴，即，
∵为的中点，即，，，
∴，
∴，
∴点为的中点，
在，中，是的中线，
∴，
∵，即，，
∴，且，，
∴，即，
∴，
∴，
∵，
∴，
故答案为：．
解答题（本题有8小题，第17~19题每题6分，第20、21题每题8分，
第22、23题每题10分，第24题12分，共66分）
17．（1）分解因式：．
（2）解不等式：．
【答案】（1）；（2）．
【分析】（1）利用提取公因式法分解因式即可；
（2）按照解不等式的一般步骤求解即可．
【详解】解：（1）；
（2）
去括号，得，
移项合并，得．
18．小明解方程的过程如图．
(1)请指出他解答过程中的错误，并写出正确的解答过程;
(2)解方程，请写出正确的解答过程．
【答案】（1）见解析；（2）见解析
【详解】解：（1）小明的解法有三处错误，步骤①去分母有误；步骤②去括号有误；步骤⑥少检验；
正确解法为：方程两边乘以x，得，
去括号，得，
移项，合并同类项，得，
解得，
经检验是分式方程的解，
则原分式方程的解为；
（2）去分母得：，
解得，
经检验是分式方程的解．
19．如图，在中，．
（1）用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E，再连接BD
（保留作图痕迹，不要求写作法和证明）；
（2）在（1）题的基础上，求证：．
【答案】（1）见解析；（2）见解析
【分析】（1）直接利用线段垂直平分线的作法得出答案；
（2）直接利用中垂线的性质结合角平分线的性质得出DC=DE．
【详解】（1）解：如图所示：DE就是要求作的AB边上的中垂线；
（2）证明：∵DE是AB边上的中垂线，∠A=30°，
∴AD=BD，
∴∠ABD=∠A=30°，
∵∠C=90°，
∴∠ABC=90°-∠A=90°-30°=60°，
∴∠CBD=∠ABC-∠ABC=60°-30°=30°，
∴∠ABD=∠CBD，
∵DC⊥CB，DE⊥EB，
∴CD=DE．
20．阅读下面的文字，完成解答过程．
(1) ，，，
挍照等号右边的形式直接写出结果：__________．
尝试并计算：；
根据上述方法计算：；
[拓展]观察：，，，
计算：；
【答案】(1)
(2)
(3)
(4)
【分析】本题主要考查有理数的混合运算，
（1）分析所给的等式的形式，从而可求解即可；
（2）利用所给的式子的形式，把各项进行拆项，从而可求解；
（3）仿照所给的式子的形式进行求解即可；
（4）根据所给的式子的形式进行求解即可．解答的关键是对相应的运算法则的掌握．
【详解】（1）由题意得：，
故答案为：；
（2）
；
（3）
；
（4）
．
校团委招聘学生会干部，根据实际需要，对应聘者分别从经验、能力、态度三个方面进行了测试．
其中甲、乙、丙三名应聘者的测试成绩如表．（单位：分）三名应聘者测试成绩

如果将经验、能力和态度三项得分按的比例确定最后的得分，请你算出甲的最终得分．
如果学生会较看重学生的能力、将经验、能力和态度三项得分按的比例确定最后的得分，
请算出甲的最终得分．
校团委按照（2）中的成绩计算方法，将每位应聘者的最后成绩绘制成如图所示的频数分布直方图
（每组分数段均包含左端数值，不包含右端数值、最右边一组分数为：），
并决定录用最终得分在80分及以上的应聘者，问甲、乙、丙三人能否被录用、请说明理由，
并求出本次招聘学生会干部的录用率．
【答案】(1)甲的最终得分为分
(2)甲的最终得分为分
(3)乙和丙都能被录用，见解析，本次招聘学生会干部的录用率为
【分析】（1）根据加权平均数进行计算即可求解；
（2）根据加权平均数进行计算即可求解；
（3）按照（2）的权数，根据加权平均数计算乙和丙的成绩，结合题意可得乙和丙都能被录用，根据条形统计图得出大于80分的人数，除以总人数即可求解．
【详解】（1）解：（分），
答：甲的最终得分为76分；
（2）解：（分），
答：甲的最终得分为73.25分；
（3）乙和丙都能被录用，理由如下：
乙的最终得分为（分），
丙的最终得分为（分），
．
答：乙和丙都能被录用，本次招聘学生会干部的录用率为．
消防车是救援火灾的主要装备，图①是一辆登高云梯消防车的实物图，
图②是其工作示意图，起重臂（20米30米）是可伸缩的，
且起重臂可绕点A在一定范围内上下转动张角，
转动点A距离地面的高度为4米．

当起重臂的长度为24米，张角时，
云梯消防车最高点C距离地面的高度的长为__________米．
某日一栋大楼突发火灾，着火点距离地面的高度为26米，该消防车在这栋楼下能否实施有效救援？
请说明理由（参考数据：）
（提示：当起重臂伸到最长且张角最大时，云梯顶端C可以达到最大高度）
【答案】(1)16
(2)能
【分析】（1）过点作，在中求出的长度，然后计算即可；
（2）当起重臂最长，转动张角最大时，同样求出的长度，与26米比较即可.
【详解】（1）解：如图，过点作，
由题意的：，，
，
，
在中，
，
，
米．
故答案为：16；
（2）解：当起重臂最长，转动张角最大时，
即：米，，
，
，
米．
，
能实施有效救援．
23．如图，在平面直角坐标系中，二次函数的图象与x轴交于，两点，与y轴交于C点，点P是直线下方抛物线上一动点．

求这个二次函数的解析式；
当动点P运动到什么位置时，使四边形的面积最大，
求出此时四边形的面积最大值和P的坐标．
【答案】(1)；
(2)当时，四边形ABCP的最大值是，．
【分析】对于（1），直接将点A，B的坐标代入关系式，即可求出答案；
对于（2），分别求出各线段的长，再表示出点P的坐标，然后根据列出二次函数，整理为顶点式，再讨论极值即可得出答案．
【详解】（1）∵二次函数的图象与x轴交于两点，

∴，
解得：，
∴这个二次函数的表达式为：；
（2）当时，，
∴点．
∵，，
∴，，．
设点P的坐标为，
，
．
∵，
∴当时，四边形的最大值是，
此时点P的坐标为．
24 .小贺在复习浙教版教材九上第81页第5题后，进行变式、探究与思考：
如图1，的直径垂直弦AB于点E，且，．

复习回顾：求的长．
探究拓展：如图2，连接，点G是上一动点，连接，延长交的延长线于点F．
① 当点G是的中点时，求证：；
② 设，，请写出y关于x的函数关系式，并说明理由；
③ 如图3，连接，当为等腰三角形时，请计算的长．
【答案】(1)；
(2)①见解析；②；③的长为或．
【分析】（1）先求得的直径为10，再利用垂径定理求得，在中，利用勾股定理即可求解；
（2）①连接，由点G是的中点，推出，根据等角的余角相等即可证明结论成立；
②利用勾股定理求得，利用垂径定理得到，推出，证明，利用相似三角形的性质即可求解；
③分两种情况讨论，当和时，证明，利用相似三角形的性质求解即可.
【详解】（1）解：连接，

∵的直径垂直弦AB于点E，且，，
∴，，
∴，，
在中，，
∴；
（2）解：①连接，

∵点G是的中点，
∴，
∴，
∵的直径垂直弦AB于点E，
∴，
∴，
∴；
②∵，，，
∴，

∵的直径垂直弦AB于点E，
∴，
∴，
∵，
∴，
∴，即，
∴；
③当时，

在中，，
∴，
∵，
∴，
∴，即，
∴；
当时，

在中，，
在中，，
∴，
同理，
∴，即，
∴；
综上，的长为或．
解：方程两边同乘x得 ①
去括号得 ②
合并同类项得 ③
移项得 ④
解得 ⑤
原方程的解为： ⑥
项目
应聘者
甲
乙
丙
经验
能力
态度