




微重点08 立体几何中的动态问题(3大考点+强化训练)-2024年高考数学重难点培优精讲
展开一、注意基础知识的整合、巩固。二轮复习要注意回归课本,课本是考试内容的载体,是高考命题的依据。浓缩课本知识,进一步夯实基础,提高解题的准确性和速度
二、查漏补缺,保强攻弱。在二轮复习中,对自己的薄弱环节要加强学习,平衡发展,加强各章节知识之间的横向联系,针对“一模”考试中的问题要很好的解决,根据自己的实际情况作出合理的安排。
三、提高运算能力,规范解答过程。在高考中运算占很大比例,一定要重视运算技巧粗中有细,提高运算准确性和速度,同时,要规范解答过程及书写。
四、强化数学思维,构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结,以便于同学们在刷题时做到思路清晰,迅速准确。
五、解题快慢结合,改错反思。审题制定解题方案要慢,不要急于解题,要适当地选择好的方案,一旦方法选定,解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确,还要优化解题过程,提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
微重点08 立体几何中的动态问题(3大考点+强化训练)
“动态”问题是高考立体几何问题最具创新意识的题型,它渗透了一些“动态”的点、线、面等元素,给静态的立体几何题赋予了活力,题型更新颖.同时,由于“动态”的存在,也使立体几何题更趋多元化,将立体几何问题与平面几何中的解三角形问题、多边形面积问题以及解析几何问题之间建立桥梁,使得它们之间灵活转化.
知识导图
考点分类讲解
考点一:动点轨迹问题
规律方法 解决与几何体有关的动点轨迹问题的方法
(1)几何法:根据平面的性质进行判定.
(2)定义法:转化为平面轨迹问题,用圆锥曲线的定义判定或用代数法进行计算.
(3)特殊值法:根据空间图形线段长度关系取特殊值或位置进行排除.
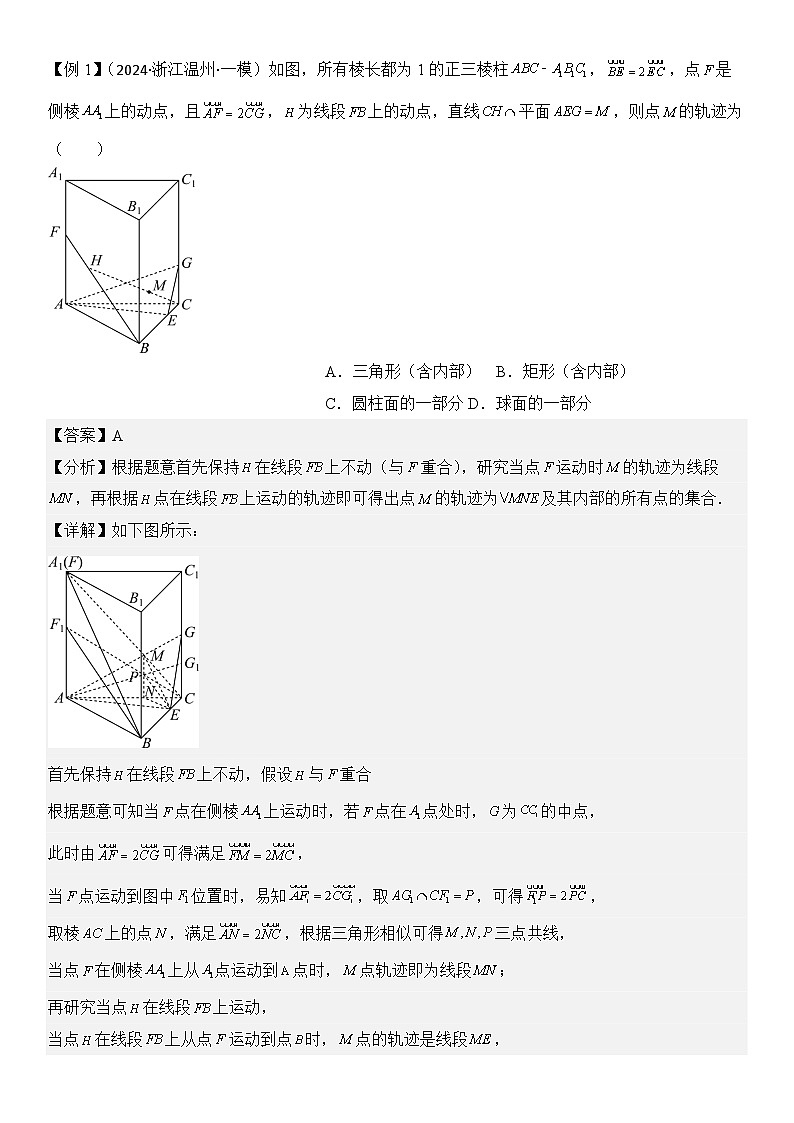
【例1】(2024·浙江温州·一模)如图,所有棱长都为1的正三棱柱,,点是侧棱上的动点,且,为线段上的动点,直线平面,则点的轨迹为( )
A.三角形(含内部)B.矩形(含内部)
C.圆柱面的一部分D.球面的一部分
【变式1】(多选)(23-24高三上·贵州安顺·期末)如图,在棱长为2的正方体中,点E、F、G、H分别为棱、、、的中点,点M为棱上动点,则( )
A.点E、F、G、H共面B.的最小值为
C.点B到平面的距离为D.
【变式2】(2023·贵州·一模)如图,已知正方体的棱长为2,M,N,P分别为棱的中点,Q为该正方体表面上的点,若M,N,P,Q四点共面,则点Q的轨迹围成图形的面积为 .
【变式3】(2023·宁波联考)正方体ABCD-A1B1C1D1的棱长为1,点P满足eq \(BP,\s\up6(→))=λeq \(BC,\s\up6(→))+μeq \(BB1,\s\up6(—→))(λ,μ∈R),则下列说法正确的有( )
A.若λ+μ=1,则A1P⊥AD1
B.若λ+μ=1,则三棱锥A1-PDC1的体积为定值
C.若点P总满足PA⊥BD1,则动点P的轨迹是一条直线
D.若点P到点A的距离为eq \r(3),则动点P的轨迹是一个面积为π的圆
考点二:折叠、展开问题
规律方法 画好折叠、展开前后的平面图形与立体图形,抓住两个关键点:不变的线线关系、不变的数量关系.
【例2】(2024·河南·模拟预测)为体现市民参与城市建设、共建共享公园城市的热情,同时搭建城市共建共享平台,彰显城市的发展温度,某市在中心公园开放长椅赠送点位,接受市民赠送的休闲长椅.其中观景草坪上一架长椅因其造型简单别致,颇受人们喜欢(如图1).已知和是圆的两条互相垂直的直径,将平面沿翻折至平面,使得平面平面(如图2)此时直线与平面所成角的正弦值为( )
A.B.C.D.
【变式1】(22-23高三上·浙江·开学考试)如图,矩形中,,将沿直线翻折成,若为线段的点,满足,则在翻折过程中(点不在平面内),下面四个选项中正确的是( )
A.平面
B.点在某个圆上运动
C.存在某个位置,使
D.线段的长的取值范围是
【变式2】(2024高三·全国·专题练习)如图1,在等边中,点分别为边上的动点且满足,记.将沿DE翻折到的位置,使得平面平面DECB,连接MB,MC,如图2,N为MC的中点.
(1)当平面MBD时,求的值.
(2)随着的值的变化,二面角的大小是否改变?若是,请说明理由;若不是,请求出二面角的正弦值.
【变式3】(2023·邵阳模拟)如图所示,在矩形ABCD中,AB=eq \r(3),AD=1,AF⊥平面ABCD,且AF=3,点E为线段CD(除端点外)上的动点,沿直线AE将△DAE翻折到△D′AE,则下列说法中正确的是( )
A.当点E固定在线段CD的某位置时,点D′的运动轨迹为球面
B.存在点E,使AB⊥平面D′AE
C.点A到平面BCF的距离为eq \f(\r(3),2)
D.异面直线EF与BC所成角的余弦值的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(13),13),\f(\r(10),10)))
考点三:最值、范围问题
规律方法 在动态变化过程中产生的体积最大、距离最大(小)、角的范围等问题,常用的解题思路是
(1)直观判断:在变化过程中判断点、线、面在何位置时,所求的量有相应最大、最小值.
(2)函数思想:通过建系或引入变量,把这类动态问题转化为目标函数,从而利用代数方法求目标函数的最值.
【例3】(多选)(2023·鞍山模拟)如图,正方体ABCD-A1B1C1D1的棱长为1,P是线段BC1上的动点,则下列结论正确的是( )
A.四面体PA1D1A的体积为定值
B.AP+PC的最小值为2eq \r(2)
C.A1P∥平面ACD1
D.直线A1P与AC所成的角的取值范围是eq \b\lc\[\rc\](\a\vs4\al\c1(0,\f(π,3)))
【变式1】(2023·青岛模拟)三面角是立体几何的基本概念之一,而三面角余弦定理是解决三面角问题的重要依据.三面角P-ABC是由有公共端点P且不共面的三条射线PA,PB,PC以及相邻两射线间的平面部分所组成的图形,设∠APC=α,∠BPC=β,∠APB=γ,二面角A-PC-B为θ,由三面角余弦定理得cs θ=eq \f(cs γ-cs α·cs β,sin α·sin β).在三棱锥P-ABC中,PA=6,∠APC=60°,∠BPC=45°,∠APB=90°,PB+PC=6,则三棱锥P-ABC体积的最大值为( )
A.eq \f(27\r(2),4) B.eq \f(27,4) C.eq \f(9,2) D.eq \f(9,4)
【变式2】(23-24高三下·北京·开学考试)正方体的棱长为1,动点在线段上,动点在平面上,且平面.线段长度的取值范围是( )
A.B.C.D.
【变式3】(2023·黑龙江哈尔滨·三模)已知四棱锥的底面为正方形,底面,点是线段上的动点,则直线与平面所成角的最大值为( )
A.B.C.D.
强化训练
一、单选题
1.(2023·云南保山·二模)已知正方体,Q为上底面所在平面内的动点,当直线与的所成角为45°时,点Q的轨迹为( )
A.圆B.直线C.抛物线D.椭圆
2.(2023·全国·三模)在平面直角坐标系中,为圆上的动点,定点.现将轴左侧半圆所在坐标平面沿轴翻折,与轴右侧半圆所在平面成的二面角,使点翻折至,仍在右侧半圆和折起的左侧半圆上运动,则,两点间距离的取值范围是( )
A.B.C.D.
3.(2024·全国·模拟预测)如图,已知矩形ABCD中,E为线段CD上一动点(不含端点),记,现将沿直线AE翻折到的位置,记直线CP与直线AE所成的角为,则( )
A.B.C.D.
4.(2023·上海宝山·二模)在空间直角坐标系中,已知定点,和动点.若的面积为,以为顶点的锥体的体积为,则的最大值为( )
A.B.C.D.
5.(23-24高三上·河北衡水·阶段练习)正三棱柱中,为的中点,为棱上的动点,为棱上的动点,且,则线段长度的取值范围为( )
A.B.
C.D.
6.(23-24高三下·山西·阶段练习)在棱长为4的正方体中,是的中点,是上的动点,则三棱锥外接球半径的最小值为( )
A.3B.C.D.
7.(2023·陕西咸阳·模拟预测)如图,点是棱长为2的正方体的表面上一个动点,则以下不正确的是( )
A.当在平面上运动时,四棱锥的体积不变
B.当在线段上运动时,与所成角的取值范围是
C.使直线与平面所成的角为的点的轨迹长度为
D.若是的中点,当在底面上运动,且满足平面时,长度的最小值是
8.(2023·吉林长春·模拟预测)四棱柱中,侧棱底面,,,,侧面为正方形,设点O为四棱锥外接球的球心,E为上的动点,则直线与所成的最小角的正弦值为( )
A.B.C.D.
二、多选题
1.(23-24高三下·江苏苏州·开学考试)在正方体中, 点为棱上的动点, 则( )
A.平面平面
B.平面平面
C.与所成角的取值范围为
D.与平面所成角的取值范围为
2.(2023·全国·模拟预测)如图①,四边形ABCD是两个直角三角形拼接而成,,,,.现沿着BD进行翻折,使平面平面BCD,连接AC,得到三棱锥(如图②),则下列选项中正确的是( )
A.平面平面ACD
B.二面角的大小为60°
C.异面直线AD与BC所成角的余弦值为
D.三棱锥外接球的表面积为
3.(2023·全国·模拟预测)如图1,矩形由正方形与拼接而成.现将图形沿对折成直二面角,如图2.点(不与重合)是线段上的一个动点,点在线段上,点在线段上,且满足,,则( )
图1 图2
A.B.
C.的最大值为D.多面体的体积为定值
三、填空题
1.(2023·河南·模拟预测)如图,在棱长为1 的正方体中,是棱 (不包含端点)上一动点,则三棱锥 的体积的取值范围为 .
2.(2023·江苏淮安·模拟预测)某同学参加课外航模兴趣小组活动,学习模型制作.将一张菱形铁片进行翻折,菱形的边长为1,,E是边上一点,将沿着DE翻折到位置,使平面面,则点A与之间距离最小值是 .
3.(23-24高三上·河北保定·期末)如图,在棱长为8的正方体中,是棱上的一个动点,给出下列三个结论:①若为上的动点,则的最小值为;②到平面的距离的最大值为;③为的中点,为空间中一点,且与平面所成的角为,与平面所成的角为,则在平面上射影的轨迹长度为,其中所有正确结论的序号是 .
四、解答题
1.(2023·河南·二模)如图所示,正六棱柱的底面边长为1,高为,为线段上的动点.
(1)求证:平面;
(2)设直线与平面所成的角为,求的取值范围.
2.(2024高三·全国·专题练习)如图,在正方体中,分别是、的中点.
(1)求与所成的角;
(2)设,在正方形内(或上),是否存在点使得三棱锥的体积为1?若存在,求出动点的轨迹;若不存在,说明理由.
3.(2023·广西南宁·模拟预测)如图,在矩形中,,,点是边上的动点,沿将翻折至,使二面角为直二面角.
(1)当时,求证:;
(2)当时,求二面角的正弦值.
4.(22-23高三下·安徽·阶段练习)如图,在四棱锥中,所有棱长都相等,,分别是棱,的中点,是棱上的动点,且.
(1)若,证明:平面.
(2)求平面与平面夹角余弦值的最大值.
5.(2023·全国·模拟预测)如图,在直三棱柱中,,,垂直于平面.点,,分别为边,,上的动点(不包括顶点),且满足.
(1)求三棱锥的体积的最大值;
(2)记平面与平面所成的锐二面角为,当最小时,求的值,并说明点所处的位置.
微重点09 截面、交线问题(3大考点+强化训练)-2024年高考数学重难点培优精讲(新高考专用): 这是一份微重点09 截面、交线问题(3大考点+强化训练)-2024年高考数学重难点培优精讲(新高考专用),文件包含微重点09截面交线问题3大考点+强化训练原卷版docx、微重点09截面交线问题3大考点+强化训练解析版docx等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
微重点07 球的切接问题(2大考点+强化训练)-2024年高考数学重难点培优精讲(新高考专用): 这是一份微重点07 球的切接问题(2大考点+强化训练)-2024年高考数学重难点培优精讲(新高考专用),文件包含微重点07球的切接问题2大考点+强化训练原卷版docx、微重点07球的切接问题2大考点+强化训练解析版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
微重点06子数列与增减项问题(3大考点+强化训练)-2024年高考数学重难点培优精讲(新高考专用): 这是一份微重点06子数列与增减项问题(3大考点+强化训练)-2024年高考数学重难点培优精讲(新高考专用),文件包含微重点06子数列与增减项问题3大考点+强化训练原卷版docx、微重点06子数列与增减项问题3大考点+强化训练解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。












