




所属成套资源:2021年新高考数学名校地市选填压轴题好题汇编
2021年新高考数学名校地市选填压轴题好题汇编(二十)(原卷版+解析版)
展开
这是一份2021年新高考数学名校地市选填压轴题好题汇编(二十)(原卷版+解析版),文件包含2021年新高考数学名校地市选填压轴题好题汇编二十原卷版docx、2021年新高考数学名校地市选填压轴题好题汇编二十解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
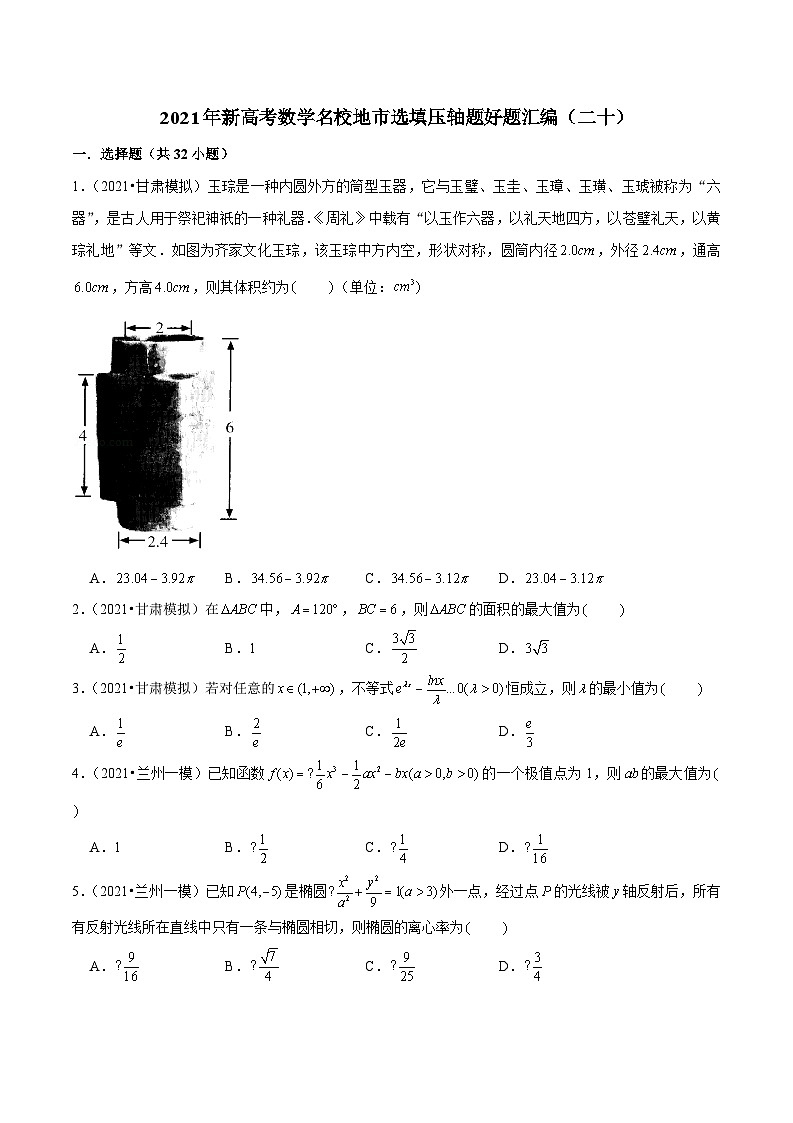
1.(2021•甘肃模拟)玉琮是一种内圆外方的筒型玉器,它与玉璧、玉圭、玉璋、玉璜、玉琥被称为“六器”,是古人用于祭祀神祇的一种礼器.《周礼》中载有“以玉作六器,以礼天地四方,以苍璧礼天,以黄琮礼地”等文.如图为齐家文化玉琮,该玉琮中方内空,形状对称,圆筒内径,外径,通高,方高,则其体积约为 (单位:
A.B.C.D.
2.(2021•甘肃模拟)在中,,,则的面积的最大值为
A.B.1C.D.
3.(2021•甘肃模拟)若对任意的,不等式恒成立,则的最小值为
A.B.C.D.
4.(2021•兰州一模)已知函数的一个极值点为1,则的最大值为
A.1B.C.D.
5.(2021•兰州一模)已知是椭圆外一点,经过点的光线被轴反射后,所有有反射光线所在直线中只有一条与椭圆相切,则椭圆的离心率为
A.B.C.D.
6.(2021•甘肃模拟)设,是双曲线的左、右焦点,一条渐近线方程为,为双曲线上一点,且,则△的面积等于
A.6B.12C.D.
7.(2021•甘肃模拟)若函数为定义在上的偶函数,当时,,则不等式的解集为
A.B.
C.,,D.,,
8.(2021•甘肃模拟)下列四个命题:
①命题“,”的否定是“,”
②,是两个不同的平面,,,,则.
③函数为上的增函数.
④.
其中真命题的个数是
A.0个B.1个C.2个D.3个
9.(2021•巴宜区校级一模)已知是上可导的图象不间断的偶函数,导函数为,且当时,满足,则不等式的解集为
A.B.C.D.
10.(2021•新疆模拟)已知函数.若存在实数,且,使得,则实数的取值范围为
A.,B.,,
C.,D.,,
11.(2021•新疆模拟)已知点为双曲线的左焦点.直线与双曲线的左支交于点,且为坐标原点),则此双曲线的离心率为
A.B.C.D.
12.(2021•乌鲁木齐模拟)四面体的所有棱长都相等,其顶点都在球的球面上,过点,,作平面,平面截此四面体所得截面面积为,则球的表面积为
A.B.C.D.
13.(2021•乌鲁木齐模拟)设点,分别是双曲线的两个焦点,若双曲线上存在点,使,且,则双曲线的离心率为
A.B.2C.D.
14.(2021•贵州模拟)已知函数,有如下四个结论:
①函数的图象关于点对称;
②函数的图象的一条对称轴为;
③,都有,则的最小值为3;
④,使得,则的最大值为.
其中所有正确结论的编号是
A.①②B.①③C.①④D.②③
15.(2021•贵州模拟)已知函数有如下四个结论:
①函数的图象关于点对称;
②函数的图象的一条对称轴为;
③,都有,则的最小值为3;
④,使得,则的最大值为,其中所有正确结论的编号是
A.①③B.②④C.①②③D.②③④
16.(2021•遵义一模)双曲线上一点到右焦点距离为6,为左焦点,则的角平分线与轴交点坐标为
A.B.C.D.
17.(2021•遵义一模),不等式恒成立,则的最大值为
A.B.0C.D.
18.(2021•贵州模拟)我们学过用角度制与弧度制度量角,最近,有学者提出用“面度制”度量角,因为在半径不同的同心圆中,同样的圆心角所对扇形的面积与半径平方之比是常数,从而称这个常数为该角的面度数,这种用面度作为单位来度量角的单位制,叫做面度制.在面度制下,角的面度数为,则
A.B.C.D.
19.(2021•榆林模拟)阳马,中国古代算数中的一种几何体,它是底面为长方形,两个三角面与底面垂直的四棱锥.已知在阳马中,平面,,且阳马的体积为9,则阳马外接球表面积的最小值是
A.B.C.D.
20.(2021•贵州模拟)已知,,,则
A.B.C.D.
21.(2021•贵州模拟)如图,在正方体中,点在棱上,且,是线段上一动点,现给出下列结论:
①;
②存在一点,使得;
③三棱锥的体积与点的位置无关.
其中正确结论的个数为
A.0B.1C.2D.3
22.(2021•贵州模拟)已知函数是定义在上的奇函数,其导函数为,且对任意实数都有,则不等式的解集为
A.B.C.D.
23.(2021•新乡二模)在四面体中,平面,且,.若四面体外接球的半径为.则与平面所成角的正切值为
A.B.C.2D.3
24.(2021•昆明一模)饮酒驾车、醉酒驾车是严重危害《道路交通安全法》的违法行为,将受到法律处罚.检测标准:“饮酒驾车:车辆驾驶人员血液中的酒精含量大于或者等于,小于的驾驶行为;醉酒驾车:车辆驾驶人员血液中的酒精含量大于或者等于的驾驶行为.”据统计,停止饮酒后,血液中的酒精含量平均每小时比上小时降低.某人饮酒后测得血液中的酒精含量为,若经过小时,该人血液中的酒精含量小于,则的最小值为 (参考数据:
A.7B.8C.9D.10
25.(2021•昆明一模)已知函数,,的一个零点是,图象的一条对称轴是直线,下列四个结论:
①;
②;
③;
④直线是图象的一条对称轴.
其中所有正确结论的编号是
A.①②B.①③C.②④D.③④
26.(2021•大理州二模)已知四面体所有顶点都在球的球面上,且平面,若,,,则球的表面积为
A.B.C.D.
27.(2021•大理州二模)设抛物线的焦点为,过的直线与抛物线交于点,,与圆交于点,,其中点,在第一象限,则的最小值为
A.B.C.D.
28.(2021•大理州二模)已知函数,,若对任意的,,存在唯一的,,使得,则实数的取值范围是
A.,B.,C.,D.,
29.(2021•云南一模)已知双曲线的中心在坐标原点,焦点在轴上,点,在双曲线的一条渐近线上.若以双曲线的实轴为直径作圆,该圆经过点,则双曲线的方程为
A.B.C.D.
30.(2021•云南一模)已知是自然对数的底数,当,时,若关于的不等式的解集非空,则实数的取值范围为
A.,B.,C.,D.,
31.(2021•云南一模)的三内角,,对的边分别为,,.若,则
A.B.C.D.
32.(2021•海南三模)直四棱柱的所有棱长均相等,,是上一动点,当取得最小值时,直线与所成角的余弦值为
A.B.C.D.
二.多选题(共1小题)
33.(2021•海南三模)如图所示,“嫦娥五号”月球探测器飞行到月球附近时,首先在以月球球心为圆心的圆形轨道Ⅰ上绕月飞行,然后在点处变轨进入以为一个焦点的椭圆轨道Ⅱ上绕月飞行,最后在点处变轨进入以为圆心的圆形轨道Ⅲ绕月飞行,设圆形轨道Ⅰ的半径为,圆形轨道Ⅲ的半径为,则
A.椭圆轨道Ⅱ上任意两点距离最大为
B.椭圆轨道Ⅱ的焦距为
C.若不变,则越大,椭圆轨道Ⅱ的短轴越短
D.若不变,则越小椭圆轨道Ⅱ的离心率越大
三.填空题(共17小题)
34.(2021•甘肃模拟)函数,,有下列命题:
①的表达式可改写为;
②直线是函数图象的一条对称轴;
③函数的图象可以由函数的图象向右平移个单位长度得到;
④满足的的取值范围是,.
其中正确的命题序号是 (注把你认为正确的命题序号都填上)
35.(2021•兰州一模)如图,正方体的棱长为1,点是棱的中点,过的平面与平面平行,且与正方体各面相交得到截面多边形,则该截面多边形的周长为 .
36.(2021•兰州一模)如图,正方体的棱长为1,点在棱上,,过的平面与平面平行,且与正方体各面相交得到截面多边形,则该截面多边形的周长为 .
37.(2021•巴宜区校级一模)已知为抛物线的焦点,弦经过,且,为坐标原点,当的倾斜角等于时, .
38.(2021•新疆模拟)在棱长为2的正方体中,点是棱的中点,点是底面上的动点,且,则下列说法正确的是 .
①与所成角的大小为;
②四面体的体积为定值;
③△的面积有最小值;
④平面截正方体所得截面面积为定值.
39.(2021•乌鲁木齐模拟)已知函数在上是增函数,且存在垂直于轴的切线,则的取值范围是 .
40.(2021•贵州模拟)过圆外一点,作圆的切线,切点分别为,,我们可以把线段叫做圆的切点弦,其所在直线方程为.现过点作圆的切线,切点分别为,,则切点弦所在直线的方程为 ;若点是直线上的动点,过点作圆的切线,切点分别为,,则切点弦所在直线恒过定点 .
41.(2021•贵州模拟)卵形线是由法田天文家引入的.卵形线的定义是:线上的任何点到两个固定点,的距离的乘积等于常数,是正常数,设,的距离为,如果,就得到一个没有自交点的卵形线;如果,就得到一个双纽线;如果,就得到两个卵形线.若,.动点满足.则动点的轨迹的方程为 ;若和是轨迹与轴交点中距离最远的两点,则面积的最大值为 .
42.(2021•遵义一模)如图,正方形中,,点为中点,现将沿折起形成四棱锥,则下列命题中为真命题的是 .
①设点为中点,若,则在折起过程中,、、、四点可能共面;
②设与交于点,则在折起过程中与可能垂直;
③四棱锥体积的最大值为.
43.(2021•贵州模拟)已知圆,动圆过点,且圆与圆外切,则动圆的圆心的轨迹方程是 .
44.(2021•贵州模拟)已知函数,若函数有4个零点,则的取值范围是 .
45.(2021•黔东南州模拟)关于函数有如下四个命题:
①的定义域为,;②的最小值为;
③存在单调递减区间;④,.
其中所有真命题的序号是 .
46.(2021•昆明一模)已知中,,满足,,则的面积为 .
47.(2021•昆明一模)由正三棱锥截得的三棱台的高为,,.若三棱台的各顶点都在球的球面上,则球的表面积为 .
48.(2021•大理州二模)我们把叫“费马数”(费马是十七世纪法国数学家),设,表示数列的前项之和,则使不等式成立的最大正整数的值是 .
49.(2021•云南一模)的三内角,,对的边分别为,,.若,则 .
50.(2021•云南一模)已知是自然对数的底数,当时,关于的不等式的解集非空,则实数的取值范围为 .
相关试卷
这是一份2021年新高考数学名校地市选填压轴题好题汇编(二十五)(原卷版+解析版),文件包含2021年新高考数学名校地市选填压轴题好题汇编二十五原卷版docx、2021年新高考数学名校地市选填压轴题好题汇编二十五解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
这是一份2021年新高考数学名校地市选填压轴题好题汇编(二十二)(原卷版+解析版),文件包含2021年新高考数学名校地市选填压轴题好题汇编二十二原卷版docx、2021年新高考数学名校地市选填压轴题好题汇编二十二解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
这是一份2021年新高考数学名校地市选填压轴题好题汇编(二十三)(原卷版+解析版),文件包含2021年新高考数学名校地市选填压轴题好题汇编二十三原卷版docx、2021年新高考数学名校地市选填压轴题好题汇编二十三解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。









