2024年中考数学考前20天终极冲刺专题之几何综合练习附解析

这是一份2024年中考数学考前20天终极冲刺专题之几何综合练习附解析，共71页。试卷主要包含了解答题，实践探究题，综合题等内容，欢迎下载使用。
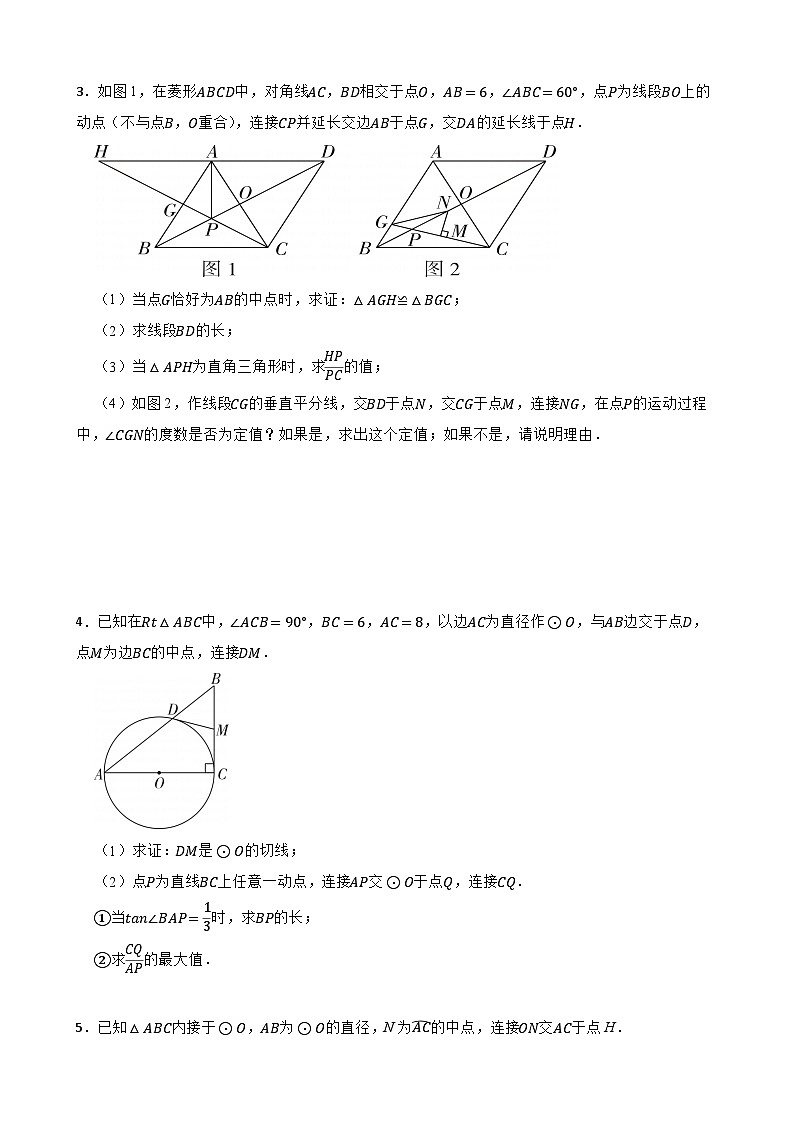
1．
（1）如图1，BP平分∠ABC,M,N分别在射线BA,BC上，若BM=BN，求证：PM=PN；
（2）如图2，在△ABC中，CP⊥CB交边AB于点P,PH⊥AC于点H．已知∠ACP=∠B,CH=2,AB=5，求△ABC的面积；
（3）如图3，在等边△ABC中，点D在边AB上，P为BA延长线上一点，E为边AC上一点，已知CA平分∠PCD,∠ADE=∠CPD,AE=2,AD=3，求PA的长．
2．已知Rt△ABC，∠ACB=90°，∠BAC=30°，点D是AC边上一点，过点D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．
（1）如图①，线段EF，CF之间的数量关系为 ，∠EFC的度数为 ；
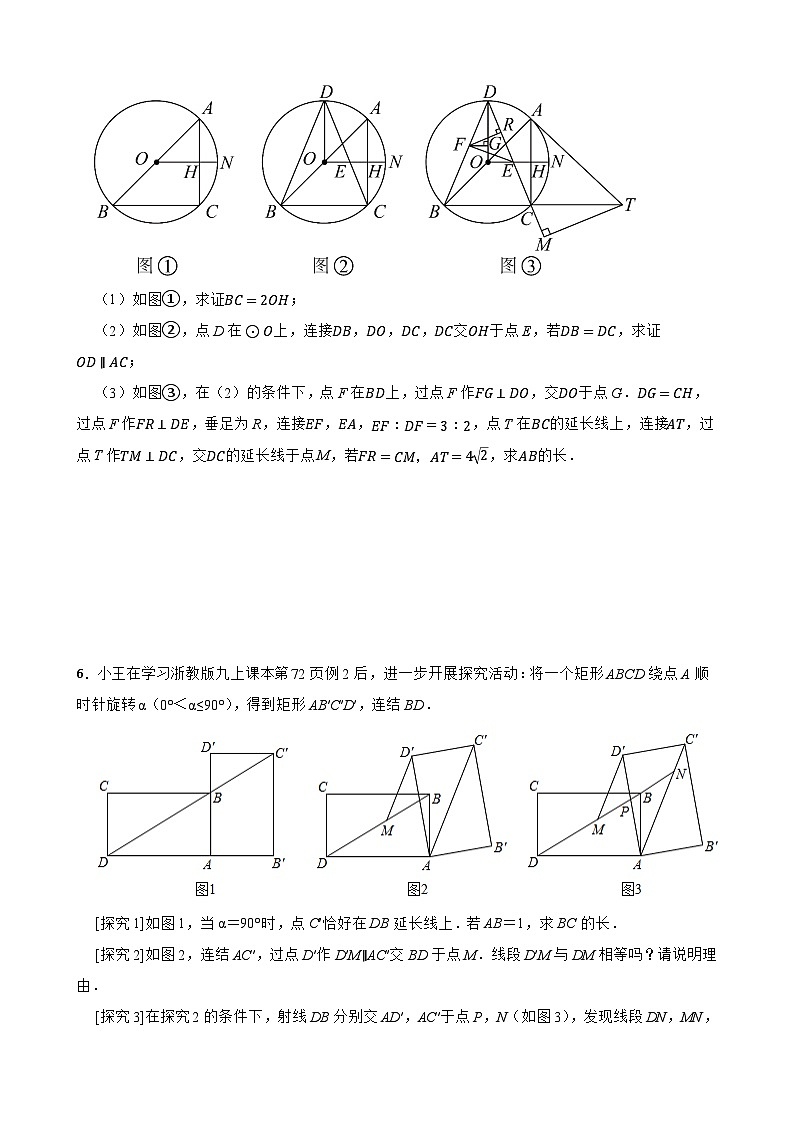
（2）如图②，将△AED绕点A按顺时针方向旋转α(0°0，
∴抛物线开口向上， ∴当x=6时，PB2+PC2的最小值是200.
故答案为：200.
【分析】【探究发现】作AE⊥BC于点E，作DF⊥BC交BC的延长线于点F，由平行四边形的性质可得AB=DC=a，AD∥BC，AD=BC=b，利用HL证明Rt△ABE≌Rt△DCF，得到BE=CF，然后根据勾股定理进行证明；
【拓展提升】延长BO到点C，使OD=BO，由中线的概念可得OA=CO，则四边形ABCD是平行四边形，由【探究发现】可知AC2+BD2=2(AB2+BC2)，即c2+(2BO)2=2(a2+b2)，化简即可；
【尝试应用】根据矩形的性质可得AB=CD=8，BC=AD=12，∠A=∠D=90°，设AP=x，则PD=12-x，PB2+PC2=AP2+AB2+PD2+CD2=2(x-6)2+200，据此求解.
14．【答案】（1）解：AE＝EP，
理由如下：取AB的中点F，连接EF，
∵F、E分别为AB、BC的中点，
∴AF＝BF＝BE＝CE，
∴∠BFE＝45°，
∴∠AFE＝135°，
∵CP平分∠DCG，
∴∠DCP＝45°，
∴∠ECP＝135°，
∴∠AFE＝∠ECP，
∵AE⊥PE，
∴∠AEP＝90°，
∴∠AEB+∠PEC＝90°，
∵∠AEB+∠BAE＝90°，
∴∠PEC＝∠BAE，
∴△AFE≌△ECP（ASA），
∴AE＝EP；
（2）解：在AB上取AF＝EC，连接EF，
由（1）同理可得∠CEP＝∠FAE，
∵AF＝EC，AE＝EP，
∴△FAE≌△CEP（SAS），
∴∠ECP＝∠AFE，
∵AF＝EC，AB＝BC，
∴BF＝BE，
∴∠BEF＝∠BFE＝45°，
∴∠AFE＝135°，
∴∠ECP＝135°，
∴∠DCP＝45°；
（3）解：作DG⊥CP，交BC的延长线于G，交CP于O，连接AG，
由（2）知，∠DCP＝45°，
∴∠CDG＝45°，
∴△DCG是等腰直角三角形，
∴点D与G关于CP对称，
∴AP+DP的最小值为AG的长，
∵AB＝4，
∴BG＝8，
由勾股定理得AG＝ 45 ，
∴△ADP周长的最小值为AD+AG＝ 4+45 ．
【解析】【分析】（1）取AB的中点F，连接EF，根据正方形的性质以及中点的概念可得AF＝BF＝BE＝CE，则∠BFE＝45°，∠AFE＝135°，根据角平分线的概念可得∠DCP＝45°，则∠ECP＝135°，推出∠AFE＝∠ECP，根据同角的余角相等可得∠PEC＝∠BAE，利用ASA证明△AFE≌△ECP，据此可得结论；
（2）AB上取AF＝EC，连接EF，由（1）同理得∠CEP＝∠FAE，证△FAE≌△CEP，得∠ECP＝∠AFE，根据线段的和差关系得BF＝BE，由等腰三角形的性质可得∠BEF＝∠BFE＝45°，则∠AFE=∠ECP＝135°，然后根据∠DCP=∠ECP-∠DCE进行计算；
（3）作DG⊥CP，交BC的延长线于G，交CP于O，连接AG，则△DCG是等腰直角三角形，点D与G关于CP对称，AP+DP的最小值为AG的长，然后利用勾股定理计算即可.
15．【答案】（1）解：∵将ΔAEB沿BE翻折到ΔBEF处，四边形ABCD是正方形，
∴AB=BF，∠BFE=∠A=90°，
∴∠BFG=90°=∠C，
∵AB=BC=BF，BG=BG，
∴Rt△BFG≌Rt△BCG(HL)；
（2）解：延长BH，AD交于Q，如图：
设FH=HC=x，
在Rt△BCH中，BC2+CH2=BH2，
∴82+x2=(6+x)2，
解得x=73，
∴DH=DC−HC=113，
∵∠BFG=∠BCH=90°，∠HBC=∠FBG，
∴ΔBFG∽ΔBCH，
∴BFBC=BGBH=FGHC，即68=BG6+73=FG73，
∴BG=254，FG=74，
∵EQ//GB，DQ//CB，
∴ΔEFQ∽ΔGFB，ΔDHQ∽ΔCHB，
∴BCDQ=CHDH，即8DQ=736−73，
∴DQ=887，
设AE=EF=m，则DE=8−m，
∴EQ=DE+DQ=8−m+887=1447−m，
∵ΔEFQ∽ΔGFB，
∴EQBG=EFFG，即1447−m254=m74，
解得m=92，
∴AE的长为92；
（3）解：（Ⅰ）当DE=13DC=2时，延长FE交AD于Q，过Q作QH⊥CD于H，如图：
设DQ=x，QE=y，则AQ=6−x，
∵CP//DQ，
∴ΔCPE∽ΔQDE，
∴CPDQ=CEDE=2，
∴CP=2x，
∵ΔADE沿AE翻折得到ΔAFE，
∴EF=DE=2，AF=AD=6，∠QAE=∠FAE，
∴AE是ΔAQF的角平分线，
∴AQAF=QEEF，即6−x6=y2①，
∵∠D=60°，
∴DH=12DQ=12x，HE=DE−DH=2−12x，HQ=3DH=32x，
在Rt△HQE中，HE2+HQ2=EQ2，
∴(1−12x)2+(32x)2=y2②，
联立①②可解得x=34，
∴CP=2x=32；
（Ⅱ）当CE=13DC=2时，延长FE交AD延长线于Q'，过D作DN⊥AB交BA延长线于N，如图：
同理∠Q'AE=∠EAF，
∴AQ'AF=Q'EEF，即6+x6=y4，
由HQ'2+HD2=Q'D2得：(32x)2+(12x+4)2=y2，
可解得x=125，
∴CP=12x=65，
综上所述，CP的长为32或65．
【解析】【分析】（1）利用全等三角形的判定方法证明即可；
（2）利用勾股定理和相似三角形的判定与性质计算求解即可；
（3）分类讨论，利用相似三角形的性质和勾股定理计算求解即可。
16．【答案】（1）解：EGFH=1，理由为：
过点A作AM∥HF交BC于点M，作AN∥EG交CD的延长线于点N，
∵四边形ABCD是正方形，
∴AB∥CD，AD∥BC，
∴四边形AMFH是平行四边形，四边形AEGN是平行四边形，
∴AM＝HF，AN＝EG，
在正方形ABCD中，AB＝AD，∠ABM＝∠BAD＝∠ADN＝90°
∵EG⊥FH，
∴∠NAM＝90°，
∴∠BAM＝∠DAN，
在△ABM和△ADN中，∠BAM＝∠DAN，AB＝AD，∠ABM＝∠ADN
∴△ABM≌△ADN
∴AM＝AN，即EG＝FH，
∴EGFH=1；
（2）nm
（3）解：∵∠ABC=60°，AB=BC，
∴ΔABC是等边三角形，
∴设AB=BC=AC=a，
过点CN⊥AB，垂足为N，交BF于点M，
则AN=BN=12a，
在RtΔBCN中，CN=BC2−BN2=a2−(12a)2=32a，
∵CN⊥AB，CE⊥BF，
∴∠ABF+∠BMN=90°，∠ECN+∠CMF=90°，
又∵∠CMF=∠BMN，
∴∠ABF=∠ECN，
∵CN⊥AB，∠DAB=90°，
∴∠DAB=∠CNE=90°，
∴ΔNCE∽ΔABF，
∴CEBF=CNAB，即CEBF=32aa=32.
【解析】【解答】解：（2）过点A作AM∥HF交BC于点M，作AN∥EC交CD的延长线于点N，
∵四边形ABCD是矩形，
∴AB∥CD，AD∥BC，
∴四边形AMFH是平行四边形，四边形AEGN是平行四边形，
∴AM＝HF，AN＝EG，
在矩形ABCD中，BC＝AD，∠ABM＝∠BAD＝∠ADN＝90°，
∵EG⊥FH，
∴∠NAM＝90°，
∴∠BAM＝∠DAN.
∴△ABM∽△ADN，
∴AMAN=ABAD，
∵AB=m，BC=AD=n，AM＝HF，AN＝EG，
∴HFEG=mn，
∴EGFH=nm；
故答案为：nm；
【分析】（1）过点A作AM∥HF交BC于点M，作AN∥EG交CD的延长线于点N，根据正方形的性质可得AB∥CD，AD∥BC，推出四边形AMFH、AEGN是平行四边形，得到AM＝HF，AN＝EG，根据同角的余角相等可得∠BAM＝∠DAN，证明△ABM≌△ADN，据此求解；
（2）过点A作AM∥HF交BC于点M，作AN∥EC交CD的延长线于点N，根据矩形的对边平行可得AB∥CD，AD∥BC，推出四边形AMFH、AEGN是平行四边形，得到AM＝HF，AN＝EG，根据同角的余角相等可得∠BAM＝∠DAN，证明△ABM∽△ADN，然后根据相似三角形的性质进行求解；
（3）易得△ABC是等边三角形，设AB=BC=AC=a，作CN⊥AB，垂足为N，交BF于点M，根据等边三角形的性质可得AN=BN=12a，利用勾股定理可得CN，根据等角的余角相等可得∠ABF=∠ECN，证明△NCE∽△ABF，然后根据相似三角形的性质进行求解.
17．【答案】（1）证明：∵DE∥BC，
∴△ADG∽△ABF，△AEG∽△ACF．
∴DGBF=AGAF，EGCF=AGAF
∴DGBF=EGCF
∵BF=CF，
∴DG= EG．
（2）解：由(1)得DG=EG，
∵CG⊥DE，
∴CE=CD=6．
∵AE=3，
∴AC=AE+CE=9．
∵DE∥BC，
∴△ADE∽△ABC．
∴DEBC=AEAC=13
（3）解：如图，延长GE交AB于点M，连结FM，作MN⊥BC，垂足为N．
在▱ABCD中，
BO=DO，∠ABC=∠ADC=45°．
∵EG∥BD，
∴由(1)得ME=GE，
∵EF⊥EG，
∴FM=FG=10，
∴∠EFM=∠EFG．
∵∠EGF=40° ，
∴∠EFG=50°．
∵FG平分∠EFC，
∴∠EFG=∠CFG=50° ，
∴∠BFM= 180°-∠EFM-∠EFG-∠CFG=30°．
∴在Rt△FMN中，MN=FMsin30°=5，FN=FMcs30°=5 3 ，
∵∠MBN=45°，MN⊥BN，
∴BN= MN=5，
∴BF=BN+FN=5+ 53．
【解析】【分析】(1)由DE∥BC，证明△ADG~ △ABF，△AEG~△ACF，根据相似比的性质列出比例式，结合BF=CF，即可得出结论；
(2)由(1)得DG=EG，CG⊥DE，求出△DCE是等腰三角形，得出EC的长，则可求出AC长，由DE∥BC，证明△ADE∽△ABC．利用三角形相似比的性质，即可求出DEBC 的值；
(3)延长GE交AB于点M，连结FM，作MN⊥BC，垂足为N，根据（1）的方法求出ME=GE，构造出等腰三角形MFG，求出MF的长，根据直角三角形的性质求出∠EFG的度数，则可求出∠CFG，然后根据平角的定义求出∠BFM=30°，最后根据含30°、45°角的特殊直角三角形，求出BN、FN的值，即可得出BF的长.
18．【答案】（1）证明：如图1，
∵△BFE 由 △BCE 折叠得到，
∴BE⊥CF ，
∴∠ECF+∠BEC=90° .
又 ∵ 四边形ABCD是正方形，
∴∠D=∠BCE=90° ，
∴∠ECF+∠CGD=90° ，
∴∠BEC=∠CGD ，
又 ∵ 正方形 ABCD，
∴BC=CD， ，
∴△BCE≌△CDG(AAS)
（2）解：如图，连接 EH ，
由（1）得 △BCE≌△CDG ，
∴CE=DG=9 ，
由折叠得 BC=BF ， CE=FE=9 ，
∴∠BCF=∠BFC .
∵ 四边形 ABCD 是正方形，
∴AD//BC ，
∴∠BCG=∠HGF ，
又 ∵∠BFC=∠HFG ，
∴∠HFG=∠HGF ，
∴HF=HG .
∵HDHF=45 ， DG=9 ，
∴HD=4 ， HF=HG=5 .
∵∠D=∠HFE=90°
∴HF2+FE2=DH2+DE2 ，
∴52+92=42+DE2 ，
∴DE=310 （ DE=−310 舍去）
（3）解：如图，连结HE，
由已知 HDHF=45 可设 DH=4m ， HG=5m ，可令 DEEC=x ，
①当点H在D点左边时，如图，
同（2）可得， HF=HG ，
∴DG=9m ，
由折叠得 BE⊥CF ，
∴∠ECF+∠BEC=90° ，
又 ∵∠D=90° ，
∴∠ECF+∠CGD=90° ，
∴∠BEC=∠CGD ，
又 ∵∠BCE=∠D=90° ，
∴△CDG∽△BCE ，
∴DGCE=CDBC ，
∵CDBC=ABBC=k ，
∴9mCE=k1 ，
∴CE=9mk=FE ，
∴DE=9mxk .
∵∠D=∠HFE=90° ，
∴HF2+FE2=DH2+DE2 ，
∴(5m)2+(9mk)2=(4m)2+(9mxk)2 ，
∴x=k2+93 （ x=−k2+93 舍去）.
∴DEEC=k2+93
②当点 H 在 D 点右边时，如图，
同理得 HG=HF ， ∴DG=m ，
同理可得 △BCE∽△CDG ，
可得 CE=mk=FE ， ∴DE=mxk ，
∵HF2+FE2=DH2+DE2 ，
∴(5m)2+(mk)2=(4m)2+(mxk)2 ，
∴x=9k2+1 （ x=−9k2+1 舍去）.
∴DEEC=9k2+1
【解析】【分析】（1）利用折叠的性质可证得BE⊥CF，利用正方形的性质可得到BC=CD，∠D=∠BCE，利用余角的性质可得到∠BEC=∠CGD；然后利用AAS可证得结论.
（2）利用全等三角形的性质可求出DG的长，利用折叠的性质可得到BC=BF，CE=EF=9；再证明∠HFG=∠HGF，利用等角对等边可证得HF=HG，结合已知条件可求出HD，HF的长；再利用勾股定理建立关于DE的方程，解方程求出DE的长.
（3）连结HE， 设DH=4m，HG=5m， DEEC=x ，①当点H在D点左边时，同理可证得HF=HG，可得到DG=9，利用折叠的性质及余角的性质可推出∠BEC=∠CGD，利用有两组对应角相等的两三角形相似，可证得△CDG∽△BCE，利用相似三角形的性质，可表示出CE的长，即可得到DE的长；然后利用勾股定理，可求出x的值，即可得到DE与EC的比值；②当点 H 在 D 点右边时，如图，同理可证得△CDG∽△BCE，利用相似三角形的性质，可表示出CE的长，即可得到DE的长；然后利用勾股定理，可求出x的值，即可得到DE与EC的比值.
19．【答案】（1）解： ∵∠ACD=∠B，∠A=∠A
∴△ADC∽△ACB
∴ADAC=ACAB
∴AC2=AD·AB
（2）解：∵四边形ABCD是平行四边形，
∴AD=BC，∠A=∠C，
又∵∠BFE=∠A，
∴∠BFE=∠C，---6分
又∵∠FBE=∠CBF，
∴△BFE∽△BCF，
∴BF2=BE·BC，
∴BC= BF2BE=163
∴AD= 163
（3）解：如图，分别延长EF，DC相交于点G，
∵四边形ABCD是菱形，
∴AB∥DC，∠BAC= 12 ∠BAD，
∵AC∥EF，
∴四边形A EGC为平行四边形，
∴AC=EG，CG=AE，∠EAC=∠G，
∵∠EDF= 12 ∠BAD，
∴∠EDF=∠BAC，
∴∠EDF=∠G，
又∵∠DEF=∠GED，
∴△EDF∽△EGD，
∴DE2=EF·EG，
又∵EG=AC=2EF，
∴DE2=2EF²，
∴DE= 2 EF，
又∵DGDF=DEEF
∴DG= 2 DF=5 2 ，
∴DC=DG-CG=5 2 -2
【解析】【分析】（1）利用两个角相等的两个三角形相似，再根据相似三角形的性质列比例式即可得出结果；
（2）由平行四边形的性质得出AD=BC，∠A=∠C，再根据两个角分别相等的两个三角形相似求出△BFE∽△BCF，于是由对应边成比例可得BF2=BE·BC，则BC的长可求，AD的长也可知；
（3）分别延长EF，DC相交于点G，由两组对边分别平行可得四边形A EGC为平行四边形，可得△EDF∽△EGD，于是由相似三角形的性质得出DE2=EF·EG，结合EG=AC=2EF， 可得DE=2EF，再根据相似三角形的性质列式，两者结合可得求得DG的长，则DC的长可求.
20．【答案】（1）解：①连接DM、MC，如图1．
∵OM是⊙P的直径，
∴∠MDO=∠MCO=90°．
∵∠AOB=90°，
∴四边形OCMD是矩形，
∴MD∥OA，MC∥OB，
∴BDDO=BMAM ， ACOC=AMBM ．
∵点M是AB的中点，即BM=AM，
∴BD=DO，AC=OC．
∵点M的坐标为（3，4），
∴OB=2OD=8，OA=2OC=6，
∴点B的坐标为（0，8），点A的坐标为（6，0）；
②在Rt△AOB中，OA=6，OB=8，
∴AB= OB2+OA2 =10．
∴BM= 12 AB=5．
∵∠OBM=∠EBD，∠BOM=∠BED，
∴△OBM∽△EBD，
∴BMBD = BOBE ，
∴54 = 8BE ，
∴BE= 325 ，
∴ME=BE﹣BM= 325 ﹣5= 75
（2）解：连接DP、PE，如图2．
∵OKMK =3，
∴OK=3MK，
∴OM=4MK，PM=2MK，
∴PK=MK．
∵OD=BD，OP=MP，
∴DP∥BM，
∴∠PDK=∠MEK，∠DPK=∠EMK．
在△DPK和△EMK中，
∠PDK=∠MEK∠DPK=∠EMKPK=MK ，
∴△DPK≌△EMK，
∴DK=EK．
∵PD=PE，
∴PK⊥DE，
∴cs∠DPK= PKPD = 12 ，
∴∠DPK=60°，
∴∠DOM=30°．
∵∠AOB=90°，AM=BM，
∴OM=BM，
∴∠OBA=∠DOM=30°
（3）解：y关于x的函数解析式为y= 21−x2 ．
提示：连接PD、OE，如图3．
设MK=t，则有OK=yt，OM=（y+1）t，
BM=OM=（y+1）t，DP=PM= (y+1)t2 ，
PK= (y+1)t2 ﹣t= (y−1)t2 ．
由DP∥BM可得△DKP∽△EKM，
则有 DPME = PKMK ，可得ME= y+1y−1 t．
∵OM是⊙P的直径，
∴∠OEM=90°，
∴OE2=OM2﹣ME2=[（y+1）t]2﹣[ y+1y−1 t]2= (y+1)2t2(y−1)2 •（y2﹣2y），
即OE= (y+1)ty−1 • y2−2y ，
BE=BM+ME=（y+1）t+ y+1y−1 t= (y+1)yty−1 ，
∴x=tan∠OBA= OEBE = y2−2yy ，
∴x2= y2−2yy2 =1﹣ 2y ，
整理得：y= 21−x2 ．
【解析】【分析】（1）①连接DM、MC，如图1，易证四边形OCMD是矩形，从而得到MD∥OA，MC∥OB，由点M是AB的中点即可得到BD=DO，AC=OC，然后利用点M的坐标就可解决问题；②根据勾股定理可求出AB的长，从而得到BM的长，要求ME的长，只需求BE的长，只需证△OBM∽△EBD，然后运用相似三角形的性质即可；（2）连接DP、PE，如图2，由 OKMK =3可得OK=3MK，进而得到OM=4MK，PM=2MK，PK=MK．易证△DPK≌△EMK，则有DK=EK．由PD=PE可得PK⊥DE，从而可得cs∠DPK= PKPD = 12 ，则有∠DPK=60°，根据圆周角定理可得∠DOM=30°．由∠AOB=90°，AM=BM可得OM=BM，即可得到∠OBA=∠DOM=30°；（3）连接PD、OE，如图3，设MK=t，则有OK=yt，OM=（y+1）t，BM=OM=（y+1）t，DP=PM= (y+1)t2 ，PK= (y−1)t2 ．由DP∥BM可得△DKP∽△EKM，则有 DPME = PKMK ，由此可得ME= y+1y−1 t，从而可求得OE= (y+1)ty−1 • y2−2y ，BE= (y+1)yty−1 ，则有x=tan∠OBA= OEBE = y2−2yy ，即x2= y2−2yy2 =1﹣ 2y ，整理得y= 21−x2 ．
21．【答案】（1）①证明：∵四边形ABCD是正方形，
∴CD = CB，∠DCA= ∠BCA= 45°，
∵CP=CP，
∴△DCP≌△BCP，
∴PD = PB；
②∠DPQ的大小不发生变化，∠DPQ=90°；
理由如下：如图所示：作PM⊥AB，PN⊥AD，垂足分别为点M、N，
∵四边形ABCD是正方形，
∴∠DAC = ∠BAC =45°，∠DAB= 90°，
∴四边形AMPN是矩形，PM= PN，
∴∠MPN = 90°，
∵PD=PQ，PM =PN，
∴Rt△DPN≌Rt△QPM(HL)，
∴∠DPN= ∠QPM，
∴∠QPN + ∠QPM = 90°，
∴∠QPN +∠DPN = 90°，
∴∠DPQ =90°；
③AQ=2OP；
理由如下：如图所示：作PE⊥AO交AB于点E，作EF⊥OB于点F，作PM⊥AE于点M，
∵四边形ABCD是正方形，
∴∠BAC=45°，∠AOB=90°，
∴∠AEP=45°，四边形OPEF是矩形，
∴PAE = ∠PEA= 45°，EF= OP，
∴PA=PE，
∵PD = PB，PD = PQ，
∴PQ= PB，
∵PM⊥AE，
∴QM=BM，AM=EM，
∴AQ= BE，
∵∠EFB= 90°，∠EBF = 45°，
∴BE=EFsin45°=2EF，
∴AQ=2OP.
（2）解：AQ=CP；
证明：∵四边形ABCD是菱形，∠ABC=60°，
∴AB=BC，AC⊥BD，DO=BO，
∴△ABC是等边三角形，AC垂直平分BD，
∴∠BAC=60°，PD=PB，
∵PD=PQ，
∴PQ=PB，
作PE∥BC交AB于点E，EG∥AC交BC于点G，如图，
则四边形PEGC是平行四边形，∠GEB=∠BAC=60°，∠AEP=∠ABC=60°，
∴EG=PC，△APE，△BEG都是等边三角形，
∴BE=EG=PC，
作PM⊥AB于点M，则QM=MB，AM=EM，
∴QA=BE，
∴AQ=CP．
【解析】【分析】（1）①利用正方形的性质求出CD = CB，∠DCA= ∠BCA= 45°，再利用全等三角形的判定与性质证明求解即可；
②利用矩形的判定与性质，全等三角形的判定与性质证明求解即可；
③利用正方形的性质求出∠BAC=45°，∠AOB=90°，再利用锐角三角函数计算求解即可；
（2）利用菱形的性质求出 AB=BC，AC⊥BD，DO=BO， 再求出 BE=EG=PC， 最后证明即可。
22．【答案】（1）证明：如图1，延长BG交AC于点H，连接AD，
∵△ABC是等边三角形，G是重心，点D为BC边的中点，
∴中线AD过点G，即A、G、D三点共线，∠BAC=∠ABC=60°，AB=AC=BC，
∴AD⟂BC，DB=DC，
∵DO=DG，
∴四边形BOCG是平行四边形，
∵AD⟂BC，
∴四边形BOCG为菱形；
（2）解：①解：直线AB是⊙O的切线，理由如下：延长BG交AC于点H，连接AD，
∵△ABC是等边三角形，G是重心，点D为BC边的中点，
∴中线AD过点G，即A、G、D三点共线，∠BAC=∠ABC=∠ACB=60°，AB=AC=BC，AH=CH，
∴BG为∠ABC的角平分线，
∴∠ABG=∠GBO=30°，
∵四边形BOCG是菱形，
∴∠CBO=∠GBC=30°，
∴∠ABO=∠ABG+∠GBC+∠CBO=90°，
∴AB⊥OB，
∴直线AB是⊙O的切线；
②证明：在优弧BC上取一点N，连接BN、CN，
由①得∠OBC=30°，
∵OB=OC，
∴∠OBC=∠OCB=30°，
∴∠BOC=180°−∠OBC−∠OCB=120°，
∴∠N=12∠BOC=60°，
∵四边形BNCM内接于⊙O，
∴∠BMC=180°−∠N=120°，
∴∠CBE+∠BCM=180°−∠BMC=60°，
∵∠ACB=∠ACF+∠BCM=60°，
∴∠ACF+∠BCM=∠CBE+∠BCM，
∴∠ACF=∠CBE，
∵BC=AC，∠BCE=∠A=60°，
∴△BEC≌△CFA(ASA)
∴AF=CE
∵AE+CE=AC
∴AE+AF=AE+CE=AC，即AE+AF为定值．
【解析】【分析】（1）延长BG交AC于点H，连接AD，先根据等边三角形的性质、重心的性质即可得到中线AD过点G，即A、G、D三点共线，∠BAC=∠ABC=60°，AB=AC=BC，进而结合题意运用平行四边形的判定即可得到四边形BOCG是平行四边形，再根据菱形的判定即可求解；
（2）①延长BG交AC于点H，连接AD，先根据等边三角形的性质、重心的性质即可得到中线AD过点G，即A、G、D三点共线，∠BAC=∠ABC=60°，AB=AC=BC，进而根据角平分线的性质得到∠ABG=∠GBO=30°，再根据菱形的性质得到∠CBO=∠GBC=30°，从而结合题意即可证明AB⊥OB，然后结合切线的判定即可求解；
②在优弧BC上取一点N，连接BN、CN，由①得∠OBC=30°，进而根据等腰三角形的性质结合三角形内角和定理即可得到∠BOC=180°−∠OBC−∠OCB=120°，从而得到∠N=12∠BOC=60°，再根据圆内接四边形的性质得到∠BMC=180°−∠N=120°，进而结合题意证明∠ACF=∠CBE，然后根据三角形全等的判定与性质即可证明△BEC≌△CFA(ASA)得到AF=CE，再结合题意即可求证。
23．【答案】（1）72；1−x
（2）证明：∵∠BDC=72°=∠C，
∴BD=BC=x，
∵∠A=∠CBD=36°，∠C=∠C，
∴△BDC∽△ABC，
∴BCAC=CDBC，
∵∠ABD=∠CBD=∠A=36°，
∴AD=BD=BC=x，
∴CD=1−x，
∴x1=1−xx，
整理，得：x2+x−1=0，
解得：x=5−12（负值已舍掉）；
经检验x=5−12是原分式方程的解．
∴底BC腰AC=5−12；
（3）解：如图，连接AC，延长AD至点E，使AE=AC，连接CE，
∵在菱形ABCD中，∠BAD=72°，AB=1，
∴∠CAD=∠ACD=36°，CD=AD=1，
∴∠EDC=∠DAC+∠ACD=72°，∠ACE=∠AEC=12(180°−∠DAC)=72°，
∴∠EDC=∠AEC，
∴CE=CD=1，
∴△ACE为黄金三角形，
∴CEAC=5−12，
∴AC=25−1=5+12．即菱形的较长的对角线的长为5+12．
【解析】【分析】（1）首先求出 ∠ABC与∠C，再根据折叠，可知∠EBD=∠CBD=12∠ABC，即可根据三角形内角和求∠BDE；由题意可知，AB=AC，由折叠可知BE=BC，即可求出AE；
（2）首先证明△BDC∽△ABC，即可知BCAC=CDBC，求出AC、BC、CD，即可证明结论；
（3）拓展应用：连接AC，延长AD至点E，使AE=AC，连接CE，首先证明△ACE为黄金三角形，即可求出AC.
24．【答案】（1）90°；1：1
（2）45°；1：2
（3）解：①解：连接BF、CE，延长CE交MN于点P，交BF于点O．
在等边△ABC中AB=AC，又∵AD⊥BC于点D，
∴D为BC的中点，
又∵M为EF的中点，N为BE的中点，
∴MN、ND分别是△BEF、△BCE的中位线，
∴MN=12BF，DN=11EC．
∵∠FAE=∠BAC=60°，
∴∠FAE+∠EAB=∠BAC+∠EAB．
∴∠FAB=∠EAC．
在△ACE和△ABF中，
AF=AE∠FAB=∠EACAB=AC，
∴△ACE≌△ABF(SAS)．
∴BF=EC．
∴MN=DN．
∴△MND为等腰三角形．
②∵△ACE≌△ABF，
∴∠ACE=∠ABF，
由(1)(2)规律可知：∠BOC=60°，
∴∠FOC=180°−∠BOC=180°−60°=120°，
又∵BF//MN，CP//DN，
∴∠MND=∠MPE=∠FOC=120°．
【解析】【解答】解：（1）①如图1所示，∵∠BAC=∠DAE，∴∠BAD=∠CAE，又∵BA=CA，DA=EA，∴△BAD≌△CAE，∴∠ABD=∠ACE，∴∠ACE+∠CBD=∠ABD+∠CBD=45°，又∵∠ACB=45°，∴∠BOC=180°-∠ACB-（ACE+∠CBD）=90°；②又△BAD≌△CAE，∴BD=CE；∴BD∶CE=1∶1；
故第1空答案为：90°；第2空答案为：1∶1；
（2）①如图2所示，∵∠ACB=∠DCE=45°，∴∠BCE=∠ACD，又∵△ACB和△DCE都是等腰直角三角形，∴ACBC=DCEC=12，∴△CAD∽△CBE，∴∠CAD=∠CBE，∴∠CAD+∠ABE=∠CBE+∠ABE=45°，∴∠A0B180°-∠BOC-（∠CAD+∠ABE）=45°；②∵△CAD∽△CBE，∴AD∶BE=AC∶BC=1∶2；
故第1空答案为：45°；第2空答案为：1∶2；
【分析】（1）可证明△BAD和△CAE全等，得出全等三角形的对应角∠ABD=∠ACE，从而得出∠OBC+∠ACO=45°，由三角形内角和定理得出∠BOC=90°；得出对应边BD=CE，∴BD∶CE=1∶1；
（2）可证明△CAD和△CBE相似，得出相似三角形的对应角∠CAD=∠CBE，从而得出∠OBA+∠CAD=45°，由三角形内角和定理得出∠AOB=45°；得出对应边AD∶BE=AC∶BC=1∶2；
（3）要证△MND是等腰三角形，可证MN=DN，由题意知MN、DN分别是△BEF、△BCE的中位线，所以只需证明BF=CE，通过证明△ACE和△ABF全等，即可证明BF=CE，所以结论得证；由（1）（2）的规律易知∠BOC=60°，所以∠FOC=120°，根据三角形中位线的性质定理，可得到NN∥BF，DN∥CE，所以可得：∠MND=∠MPE=∠FOC=120°。2.如图，在正方形ABCD中，CE⊥DF.求证：CE=DF.
证明：设CE与DF交于点O，
∵四边形ABCD是正方形，
∴∠B=∠DCF=90°，BC=CD.
∴∠BCE+∠DCE=90°.
∵CE⊥DF，
∴∠COD=90°.
∴∠CDF+∠DCE=90°.
∴∠CDF=∠BCE.
∴△CBE≌△DFC.
∴CE=DF.