2024年河北省邯郸市邱县中考数学一模试卷（含详细答案解析）

这是一份2024年河北省邯郸市邱县中考数学一模试卷（含详细答案解析），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.−a(a是有理数)表示的数是( )
A. 正数B. 负数C. 正数或负数D. 任意有理数
2.嘉嘉一家去观看杭州亚运会比赛，嘉嘉站在杭州奥体中心大门的南偏西30∘方向150m处，则( )
A. 杭州奥体中心大门在嘉嘉的南偏西30∘方向150m处
B. 杭州奥体中心大门在嘉嘉的北偏东30∘方向150m处
C. 杭州奥体中心大门在嘉嘉的北偏东60∘方向150m处
D. 杭州奥体中心大门在嘉嘉的南偏西60∘方向150m处
3.若分式x2x−1□xx−1运算结果为x，则在“□”中添加的运算符号为( )
A. +B. -C. -或÷D. +或×
4.有8张红心、m张黑桃扑克牌，背面朝上放在桌子上，从中任意摸出一张，若摸到红心的可能性比摸到黑桃的可能性大，则m的值不可能是( )
A. 10B. 5C. 3D. 1
5.四边形ABCD的边长如图所示，对角线AC的长度随四边形的形状改变而变化.当△ABC是直角三角形时，对角线AC的长为( )
A. 5
B. 2 3
C. 7
D. 4
6.对于任何整数a，多项式(3a+5)2−4都能( )
A. 被9整除B. 被a整除C. 被a+1整除D. 被a−1整除
7.已知a= 2+1，b= 2−1，则 ab+7的值为( )
A. 2B. 2 2C. 3D. 3
8.综合实践课上，嘉嘉设计的“利用直角三角形作矩形”的尺规作图过程如下：
根据嘉嘉尺规作图痕迹，完成下面的证明.
证明：∵OA=①_____，OD=OB，
∴四边形ABCD是平行四边形(②_____)(填推理依据).
又∵∠ABC=90∘，
∴四边形ABCD是矩形(③_____)(填推理依据).
①②③应该填的内容分别是( )
A. OB、对角线互相平分的四边形是平行四边形、有一个角是直角的平行四边形是矩形
B. OC、对角线互相平分的四边形是平行四边形、有一个角是直角的平行四边形是矩形
C. OD、对角线互相平分的四边形是平行四边形、有一个角是直角的平行四边形是矩形
D. OC、有一个角是直角的平行四边形是矩形、对角线互相平分的四边形是平行四边形
9.如图，点P1∼P6是⊙O的六等分点.若△P1P5P6，△P2P3P5的周长分别为C1，C2，面积分别为S1，S2，则下列正确的是( )
A. C1=C2
B. C2=2C1
C. S1=S2
D. S2=2S1
10.航天员翟志刚以7.9km/s的第一宇宙速度行走了19分35秒，由此成为“走”得最快的中国人，那么翟志刚在太空漫步的距离用科学记数法表示约为( )
A. 92.8×107mB. 9.28×108mC. 9.28×106mD. 9.29×106m
11.已知PA=3 2,PB=8，以AB为一边作正方形ABCD，使P、D两点落在直线AB的两侧.当∠APB=45∘时，PD的长是( )
A. 4 5
B. 3 6
C. 10
D. 6 2
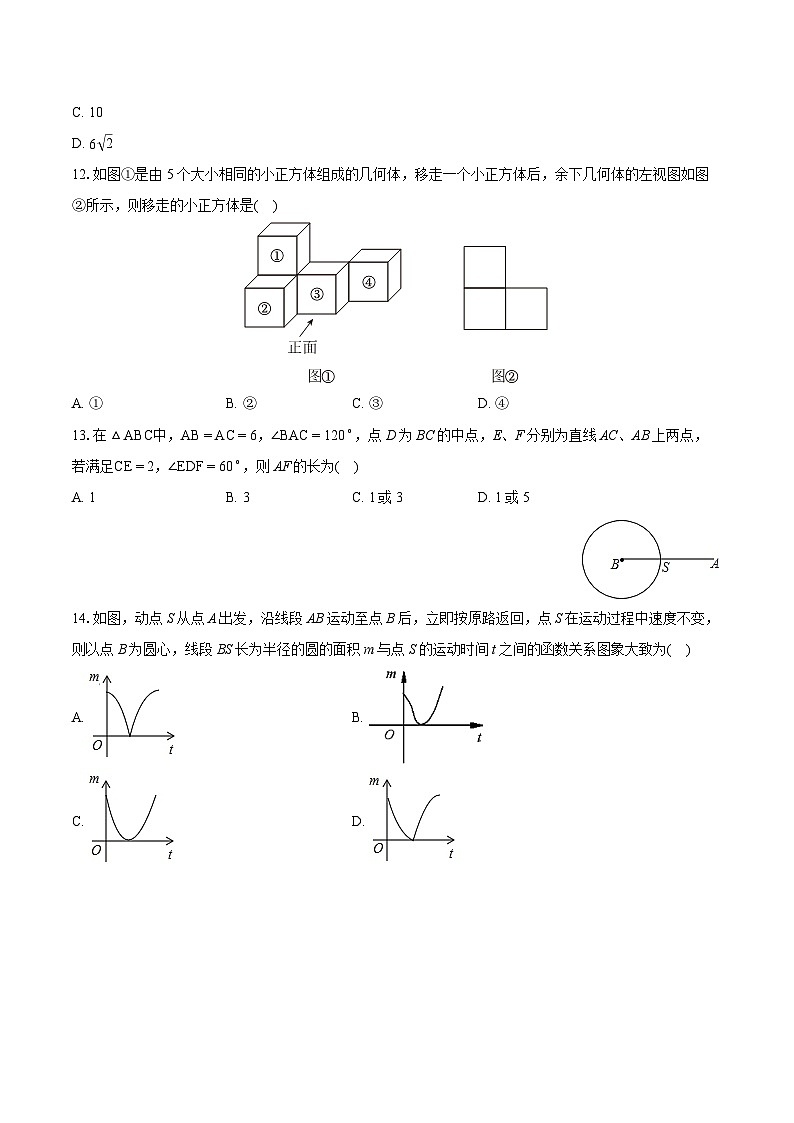
12.如图①是由5个大小相同的小正方体组成的几何体，移走一个小正方体后，余下几何体的左视图如图②所示，则移走的小正方体是( )
A. ①B. ②C. ③D. ④
13.在△ABC中，AB=AC=6，∠BAC=120∘，点D为BC的中点，E、F分别为直线AC、AB上两点，若满足CE=2，∠EDF=60∘，则AF的长为( )
A. 1B. 3C. 1或3D. 1或5
14.如图，动点S从点A出发，沿线段AB运动至点B后，立即按原路返回，点S在运动过程中速度不变，则以点B为圆心，线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )
A. B.
C. D.
15.夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示，顶点A、F分别在两条平行线上．若A、D、F在一条直线上，则∠1与∠2的数量关系是( )
A. ∠1+∠2=60∘B. ∠2−∠1=30∘C. ∠1=2∠2.D. ∠1+2∠2=90∘
16.对于一个函数：当自变量x取a时，其函数值y也等于a，我们称a为这个函数的不动点．若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点，则c的取值范围是( )
A. c<−3B. −3−14
二、填空题：本题共3小题，共10分。
17.如图，平面直角坐标系中，已知A(3,3)，B(0,−1)，将线段AB绕点A顺时针旋转90∘得到线段AB′，点B′恰好在反比例函数y=kx(k≠0)的图象上，则k值为______.
18.根据右表中的数据，写出a的值为______， b的值为______.
19.如图，过正六边形ABCDEF的顶点D作一条直线l⊥AD于点D，分别延长AB、AF交直线l于点M.N，则∠AMN=__________；若正六边形ABCDEF的面积为6，则△AMN的面积为__________.
三、解答题：本题共7小题，共72分。解答应写出文字说明，证明过程或演算步骤。
20.(本小题9分)
在伦敦奥运会举办前夕，国家足球协会举办了一次足球热身赛，其计分规则及奖励方案(每人)如下表：
当比赛进行到每队各比赛12场时，A队(11名队员)共积20分，并且没有负一场．
(1)试判断A队胜、平各几场？
(2)若每赛一场每名队员均得出场费500元，那么A队的某一名队员所得奖金与出场费的和是多少？
21.(本小题9分)
嘉嘉和琪琪玩纸片拼图游戏，他们利用图1中的三种类型的纸片可以拼出一些图形来解释某些等式，例如，由图2，我们可以得到(a+2b)(a+b)=a2+3ab+2b2.
(1)用边长为a的正方形卡片1张，边长分别为a，b的长方形卡片6张，边长为b的正方形卡片9张，拼成一个正方形，则这个正方形的边长为______；
(2)琪琪用5个长为b，宽为a的长方形按照图3方式不重叠地放在大长方形ABCD内；大长方形中未被覆盖的两个部分，设左上角的面积为S1，右下角的面积为S2，当BC的长变化时，S2−S1的值始终保持不变，求a与b的数量关系.
22.(本小题9分)
某市举办的青年冰雪体验营活动共有140人参加，为了解参加活动的人员对本次活动的满意度，随机调查了部分参加者，为本次活动打分(打分按从高到低分为5个分值：5分、4分、3分、2分、1分)，并将调查结果绘制成不完整的条形统计图(如图1)和扇形统计图(如图2).
根据以上信息，回答下列问题：
(1)本次共调查了______名参加者，并补全条形统计图；
(2)若再增补调查5位参加者，他们的打分分别为4，4，4，3，3，则增加调查人数前、后本次活动打分情况的众数是否发生改变？若改变，求这个众数；若未改变，请说明理由；
(3)在(2)的基础上，又增加了3位参加者进行打分，此时被调查的参加者打分的众数发生了改变，且唯一，求这个众数及这3位参加者的打分情况.
23.(本小题10分)
嘉嘉和淇淇在玩排球.某同学借此情境编制了一道数学题，请解答这道题.
如图，嘉嘉站在点O处练习发球(球每次出手后的运动轨迹都是形状相同的抛物线)，将球从点O正上方的点B处发出.球出手后的运动路径为抛物线，抛物线的最高点C到y轴的距离为6m，竖直高度比出手点B高出1m.已知OB=mm，排球场的边界点A到点O的水平距离OA=18m，球网高度EF=2.4m，且OE=12OA.
(1)当m=2时，排球能否越过球网？请说明理由；
(2)若嘉嘉调整起跳高度，使球在点A处落地，此时形成的抛物线记为L1，球落地后立即向右弹起，形成另一条与L1形状相同的抛物线L2，且此时排球运行的最大高度为1m，球场外有一个吉祥物玩偶MN高89m.排球向右反弹后沿L2的路径运动，若在下落的过程中，正好砸中玩偶的头部点M，求玩偶所处的位置点N与点A的距离.
24.(本小题10分)
如图，是一个半圆形桥洞的截面示意图，圆心为O，直径AB是河底截线，弦CD是水位线，CD//AB，AB=20米，OE⊥CD于点E，此时测得sin∠ODE=12.
(1)求CD的长；
(2)如图，阴影矩形是漂浮的箱子露出水面的截面图，若其长NP为10米，高PQ为2米，当点E恰在NP中点时.①画出半圆O最高点H，并直接写出点H到线段MQ的距离；
②若该箱子随水面上升1米，请判断此木箱能否通过该桥洞，并说明理由.
25.(本小题12分)
下面表格中的两组对应值满足一次函数y=kx+b，现画出了它的图象为直线l，如图1.琪琪为观察k，b对图象的影响，将上面函数中的k与b交换位置后得到另一个一次函数，设其图象为直线l′.
(1)求直线l的解析式；
(2)求直线l′的解析式，并在图中画出直线l′；
(3)若P(a,0)是x轴上的一个动点，过点P作y轴的平行线，分别交直线l，l′于点M，N.当MN=3时，求出a的值；
(4)若Q(0,m)是y轴上的一个动点，过点Q作x轴的平行线，分别与直线l，l′及y轴有三个不同的交点，且其中两点关于第三点对称，直接写出m的值.
26.(本小题13分)
在Rt△ABC中，∠ACB=90∘，AB=10，csA=45，将△ABC绕点B顺时针旋转得到△A′BC′，其中点A，C的对应点分别为点A′，C′.
(1)如图1，当点A″落在AC的延长线上时，求AA′的长；
(2)如图2，当点C′落在AB的延长线上时，连接CC′，交A′B于点M，求BM的长；
(3)如图3，连接AA′，直线CC′交AA′于点D，点E为AC的中点，连接DE.在旋转过程中，DE是否存在最大值？若存在，直接写出DE的最大值；若不存在，请说明理由.
答案和解析
1.【答案】D
【解析】解：因为a可以表示任意有理数，则−a表示的数是任意有理数．故选D.
根据字母表示数的含义即可求得，a是有理数即a可以为正有理数，也可为负有理数，也可为零．
对于未确定范围的字母取值，可以是任意有理数．
2.【答案】B
【解析】解：∵嘉嘉站在杭州奥体中心大门的南偏西30∘方向150m处，
∴杭州奥体中心大门在嘉嘉的北偏东30∘方向150m处．
故选：B.
根据方向角的定义即可解答．
本题考查方向角，理解方向角的定义是正确解答的前提．
3.【答案】C
【解析】解：当“□”中添加的运算符号为-时，
原式=x2x−1−xx−1=x2−xx−1=x
“□”中添加的运算符号为÷时，
原式=x2x−1÷xx−1=x2x−1⋅x−1x=x，
故选：C.
分式的混合运算，要注意运算顺序，式与数有相同的混合运算顺序；先乘方，再乘除，然后加减，有括号的先算括号里面的．
本题考查了分式的混合运算，熟练运用分式加减运算法则是解题的关键．
4.【答案】A
【解析】解：∵有8张红心、m张黑桃扑克牌，
∴摸到红心的可能性为88+m；
摸到黑球的可能性为m8+m，
∵摸到红心的可能性比摸到黑桃的可能性大，
∴88+m>m8+m，
∴m<8.
故m的值不可能是10.
故选：A.
分别求出摸到红球和黑球的概率，再根据摸到红球的可能性比摸到黑球的可能性大即可得出结论．
本是题考查的是可能性的大小，熟记概率公式是解题的关键．
5.【答案】C
【解析】解：当∠BAC=90∘时，
AC= BC2−AB2= 42−32= 7，2+ 7>3，符合题意；
当∠ABC=90∘时，
AC= 32+42=5，2+3=5，此时线段AD、CD、AC不能组成三角形，不符合题意；
故选：C.
利用分类讨论的方法和勾股定理，可以求得AC的长，还要考虑求出的AC的长是否使得线段AD、CD、AC能组成三角形．
本题考查勾股定理，解答本题的关键是明确题意，利用数形结合的思想解答．
6.【答案】C
【解析】解：原式=(3a+5+2)(3a+5−2)=3(3a+7)(a+1)，
则对于任何整数a，多项式(3a+5)2−4都能被a+1整除．
故选C
多项式利用平方差公式分解，即可做出判断．
此题考查了因式分解-运用公式法，熟练掌握平方差公式是解本题的关键．
7.【答案】B
【解析】解：∵a= 2+1，b= 2−1，
∴ab=( 2+1)( 2−1)
=2−1
=1，
∴ ab+7= 8=2 2.
故选：B.
先根据平方差公式计算ab=1，再化简 ab+7即可．
本题考查了二次根式的混合运算，平方差公式，熟练掌握二次根式的运算法则是解题的关键．
8.【答案】B
【解析】解：∵OA=OC，OD=OB，
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).
又∵∠ABC=90∘，
∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形).
故选：B.
先证明四边形ABCD是平行四边形，再由有一个角是直角的平行四边形是矩形，即可得出结论．
本题考查了矩形的判定以及平行四边形的判定与性质等知识，熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键．
9.【答案】D
【解析】解：连接OP1，OP6，P3P4，
∵点P1∼P6是⊙O的六等分点，
∴P1P6//P2P5//P3P4，P1P6=P5P6=P2P3，P1P5=P3P5，∠P1OP6=60∘，
∴△P1OP6是等边三角形，
∴P2P5=2P1P6，
∴S2=2S△P1OP6=2S1，故D正确，C不正确；
∴两个三角形有两条边相等，一条边是2倍关系，
∴C2≠C1≠2C1，故A、B不正确．
故选：D.
连接OP1，OP6，P3P4，由于点P1∼P6是⊙O的六等分点，可得P1P6//P2P5//P3P4，P1P6=P5P6=P2P3，P1P5=P3P5，进而得出两个三角形面积之间的关系和周长之间的关系．
本题考查了正多边形和圆，解题的关键是添加辅助线得出P2P5与P1P6的数量关系．
10.【答案】C
【解析】解：7.9×(19×60+35)=9282.5(km)=9282500(m)≈9.28×106(m)，
故选：C.
根据题意列式计算后利用科学记数法表示即可．
本题考查科学记数法，结合已知条件列得正确的算式是解题的关键．
11.【答案】C
【解析】解：过P作PB的垂线，过A作PA的垂线，两条垂线相交于E，连接BE，
∵∠APB=45∘，EP⊥PB，
∴∠EPA=45∘，
∵EA⊥PA，
∴△PAE是等腰直角三角形，
∴PA=AE，
∵PA=3 2，
∴PE= AP2+AE2= (3 2)2+(3 2)2=6，
∵四边形ABCD是正方形，
∴∠EAP=∠DAB=90∘，
∴∠EAP+∠EAD=∠DAB+∠EAD，
即∠PAD=∠EAB，
∵AD=AB，PA=AE，
∴△PAD≌△EAB，
∵PB=8，PE=6，
∴PD=BE= PE2+PB2= 62+82=10，
故选：C.
过P作PB的垂线，过A作PA的垂线，两条垂线相于与E，连接BE，由∠APB=45∘可得∠EPA=45∘，可得△PAE是等腰直角三角形，即可求出PE的长，根据角的和差关系可得∠EAB=∠PAD，利用SAS可证明△PAD≌△EAB，可得BE=PD，利用勾股定理求出BE的长即可得PD的长．
本题考查正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质及勾股定理，熟练掌握相关性质并正确作出辅助线是解题关键．
12.【答案】D
【解析】解：单独移开④，
从左边看得到的图形可得：
故选：D.
根据左视图是从左边看得到的图形，可得答案．
本题考查了简单组合体的三视图，解题的关键是掌握从左边看得到的图形是左视图．
13.【答案】D
【解析】解：当点E在线段AC上时，
如图1，取AC的中点H，连接DH，此时F在BA的延长线上，
∵AB=AC，点D为BC的中点，
∴AD⊥BC，
∵∠BAC=120∘，
∴∠CAD=∠BAD=60∘，
∴∠DAF=120∘，
∵H为AC中点，
∴AH=CH=DH，
∴△ADH为等边三角形，
∴∠AHD=60∘，
∴∠DHC=120∘=∠DAF，∠ADF+∠FDH=60∘，
∵∠EDF=60∘，即∠FDH+∠EDH=60∘，
∴∠ADF=∠EDH，
在△ADF和△HDE中，
∠DAF=∠DHEAD=DH∠ADF=∠EDH，
∴△ADF≌△HDE(ASA)，
∴AF=EH，
∵AC=6，CE=2，
∴AE=4，
∵H是AC中点，
∴CH=12AC=3，
∴AF=EH=1；
当点E在AC延长线上时，如图2，
同理可得：AF=HE=CH+CE=3+2=5；
综上：AF的长为1或5，
故选：D.
分两种情况：当点E在线段AC上时或当点E在AC延长线上时，取AC的中点H，连接DH，同理证明△ADF≌△HDE，得到AF=HE，从而求解．
本题考查了等腰三角形的性质，全等三角形的判定和性质，等边三角形的判定和性质，解题的关键是适当添加辅助线，构造全等三角形，从而得到线段之间的关系．
14.【答案】C
【解析】解：设线段AB的长为b，点S的速度为a，
则S=π(b−at)2=a2πt2−2abπt+b2π=a2π(t−ba)2，
∵a2π>0，
∴在点P从A到B的运动过程中，S随t的增大而减小，此时对应的函数图象开口向上，顶点坐标为(ba,0)，
当点P从点B向点A运动时，S随着t的增大而减小，此时对应的函数图象开口向上，顶点坐标为(ba,0)，
故选C.
根据题意可以得到S与t的函数解析式，然后根据t的变化讨论S与t的函数图象，从而可以解答本题．
本题考查动点问题的函数图象，解答此类问题的关键是明确题意，找出S与t的函数解析式，利用二次函数的性质和分类讨论的数学思想解答．
15.【答案】B
【解析】【分析】
此题考查正方形的性质，等边三角形的性质，平行线的性质的有关知识.
根据正方形的性质和等边三角形的性质以及平行线的性质解答即可.
【解答】
解：∵正方形ABCD、等边三角形DEF，
∴∠BAD=90∘，∠DFE=60∘，
∵l1//l2，A、D、F在一条直线上，
∴∠1+∠BAD=∠2+∠DFE，
即∠1+90∘=∠2+60∘，
可得：∠2−∠1=30∘，
故选B.
16.【答案】C
【解析】解：由题意知二次函数y=x2+2x+c有两个相异的不动点x1、x2是方程x2+2x+c=x的两个不相等实数根，且x1、x2都小于1，
整理，得：x2+x+c=0，
由x2+x+c=0有两个不相等的实数根知：△>0，即1−4c>0①，
令y=x2+x+c，画出该二次函数的草图如下：
而x1、x2(设x2在x1的右侧)都小于1，即当x=1时，y=x2+x+c=2+c>0②，
联立①②并解得：−2故选：C.
由函数的不动点概念得出x1、x2是方程x2+2x+c=x的两个实数根，由x1<10且x=1时y>0，即可求解．
本题主要考查二次函数图象与系数的关系，解题的关键是理解并掌握不动点的概念，并据此得出关于c的不等式．
17.【答案】−6
【解析】解：作AC⊥y轴于点C，B′D⊥AC于D，如图所示，
∵∠BAB′=90∘，∠ACB=90∘，AB=AB′，
∴∠BAC+∠ABC=90∘，∠BAC+∠B′AD=90∘，
∴∠ABC=∠B′AD，
∴△ABC≌△B′AD，
∴AC=B′D，BC=AD，
∵A(3,3)，B(0,−1)，
∴BC=AD=4，AC=B′D=3，
∴CD=4−3=1，
∴B′(−1,6)，
∵点B′恰好在反比例函数y=kx(k≠0)的图象上，
∴k=−1×6=−6，
故答案为：−6.
根据题意可以求得点B′的横坐标，然后根据点B′恰好在反比例函数y=kx(k≠0)的图象上，从而可以求得k的值．
本题考查反比例函数图象上点的坐标特征、旋转的性质，解答本题的关键是明确题意，利用数形结合的思想解答．
18.【答案】8−1
【解析】解：由题意得，a=22+2×2=8，b=2n+1，n2+2n=−1，
解得n=−1，b=−1，a=8，
故答案为：8，−1.
根据表格中的对应值，得到a=22+2×2，b=2n+1，n2+2n=−1，再进行计算即可．
本题考查代数式求值，由表格中的对应值得到a=22+2×2，b=2n+1，n2+2n=−1是正确解答的关键．
19.【答案】30∘
16

【解析】【分析】
本题考查正多边形，三角形的面积等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
连接BE，CF交于点O.根据正六边形的性质，推出∠MAD=∠NAD=60∘，推出∠AMN=∠ANM=30∘，根据S△ANM=12⋅MN⋅AD=12×2×2 3OA×2OA=4 3OA2，求出OA2即可解决问题．
【解答】
解：连接BE，CF交于点O，
∵ABCDEF是正六边形，
∴∠MAD=∠NAD=60∘，
∵AD⊥MN，
∴∠ADM=∠ADN=90∘，
∴∠AMN=∠ANM=30∘
∵ABCDEF是正六边形，面积为6，
∴点O在AD上，OA=OB，△AOB的面积=1，
∴ 34⋅OA2=1，
∴OA2=4 3，
∵AD⊥MN，DM=DN= 3AD=2 3OA，
∴S△ANM=12⋅MN⋅AD=12×2×2 3OA×2OA=4 3OA2=16，
故答案为30∘，16.
20.【答案】解：(1)设A队胜利x场，
∵一共打了12场，
∴平了12−x场，
∴3x+(12−x)=20，
解得：x=4；
(2)∵每场比赛出场费500元，12场比赛出场费共6000元，
赢了4场，奖金为1500×4=6000元，
平了8场，奖金为700×8=5600元，
∴奖金加出场费一共17600元；
答：一共赢了4场，出场费加奖金一共17600元．
【解析】(1)设A队胜利x场，则平了12−x场，根据总积分为20分列出方程即可求解；
(2)根据(1)中求得胜场数和平场数计算每名队员的奖金和出场费的总和即可解题．
本题考查了一元一次方程的应用，本题中根据总场数和总积分不变，设A队胜利x场，列出方程求解是解题的关键．
21.【答案】a+3b
【解析】解：(1)边长为a的正方形卡片1张，边长分别为a，b的长方形卡片6张，边长为b的正方形卡片9张，
用这16张卡片拼成一个正方形，
∴正方形的面积为a2+6ab+9b2，
∴设正方形的边长为x，则
x2=a2+6ab+9b2，
x2=(a+3b)2，
∴x=a+3b；
故答案为：a+3b；
(2)设AD=x，
∴S1=b(x−3a)，S2=2a(x−b)，
∴S2−S1=2a(x−b)−b(x−3a)
=(2a−b)x+ab，
当2a−b=0时，S2−S1不变，
即2a=b.
(1)利用面积法求解即可；
(2)根据已知求得两部分的面积，根据题意作差，进而求得a，b关系式．
本题考查的是多项式乘以多项式，以及完全平方公式，解题的关键是熟练掌握多项式乘多项式法则，以及完全平方公式的特点．
22.【答案】20
【解析】解：(1)被调查的总人数是10÷50%=20(名)，
则得4分的人数为20−(10+2+1+1)=6(名)，
补全条形图如下：
故答案为：20；
(2)众数没有发生改变．理由如下：
增加5位参加者的打分后，统计结果是：得5分的有10人，得4分的有9人，得3分的有4人，得2分的有1人，得1分的有1人，
这组数据的众数是5，原数据的众数也是5，
由此表可知，众数没有发生改变；
(3)再增加了3位参加者之前数据的众数是5，得4分的人数比得5分的人数少1人，
则若再增加了3位参加者，众数发生改变，且唯一，
则现在的众数只能是4分，且至少有两人打分为4分，而另外一人的打分不可能是5分，可能是4，3，2，1中的任意一个，
所以这3位参加者的打分情况是4，4，4或4，4，3或4，4，2或4，4，1.
(1)由5分的人数及其所占百分比可得被调查的总人数，总人数减去其它分数度的人数求出得4分的人数即可补全图形；
(2)根据众数的定义求解即可；
(3)根据再增加了3位参加者进行打分，此时众数发生了改变，且唯一得出现在的众数只能是4分，且至少有两人打分为4分，而另外一人的打分不可能是5分，进而求解即可．
此题考查了扇形统计图和条形统计图，解题的关键是读懂统计图，获得有关信息，在获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
23.【答案】(1)球能越过球网，球不会出界，理由如下：
∵抛物线的最高点C到y轴总是保持6米的水平距离，竖直高度总是比出手点B高出1米OB=m米，
∴C(6,m+1)，
当m=2时，
则C(6,3)，B(0,2)，
∴设抛物线的表达式为y=a(x−6)2+3，
∴将点B(0,2)代入，得2=a(0−6)2+3，
解得：a=−136，
∴抛物线的表达式为y=−136(x−6)2+3；
当m=2时，抛物线的表达式为y=−136(x−6)2+3；
∵OA=18米，OE=12OA，
∴OE=9(米)，
∵球网EF高度为2.4米，
∴F(9,2.4)，
当x=9时，y=−136(9−6)2+3=2.75，
∵2.75>2.4，
∴球能越过球网；
(2)∵球每次出手后的运动轨迹都是形状相同的抛物线，且抛物线的最高点C到y轴总是保持6米的水平距离，
又∵L2是与L1形状相同的抛物线，此时排球运行的最大高度为1米，
设L2的表达式为y=−136(x−h)2+1，
将点A(18,0)代入得：0=−136(18−h)2+1，
解得：h1=12(舍去)，h2=24，
∴L2的表达式为y=−136(x−24)2+1，
当y=89时，89=−136(x−24)2+1，
解得：t1=24，t2=20(舍去)，
∴24−18=6(米).
∴玩偶所处的位置点N与点A的距离为6米．
【解析】(1)根据题意可设抛物线的表达式为y=a(a−6)2+3，再将点B的坐标代入表达式中求出函数解析式，易得F(9,2.4)，将x=9代入抛物线表达式中求出对应y值，和2.4比较即可判断球能否越过球网界；
(2)根据题意可设L2的表达式为y=−136(x−h)2+1，将点A坐标代入求得L2：y=−136(x−24)2+1，求出当y=89时x的值即可求解．
本题主要考查二次函数的应用、二次函数的图象与性质、用待定系数法求函数解析式，熟练掌握二次函数的图象与性质是解题的关键．
24.【答案】解：(1)∵AB=20米，圆心为O，
∴OA=OB=10米，
∴OD=10米，
∵OE⊥CD，CD为弦，
∴OE垂直平分CD，CE=DE，
∵sin∠ODE=12，
∴∠ODE=30∘，
∴cs∠ODE= 32，
在Rt△ODE中，DE=OD⋅cs∠ODE=10× 32=5 3(米)，
∴CD=2DE=10 3(米).
(2)①如图，延长OE交MQ于点F，交半圆O于点H，
则点H为半圆O的最高点，OH=10米，
在Rt△ODE中，∠ODE=30∘，则OE=12OD=5(米)，
∵四边形MNPQ为矩形，
∴MQ//NP，
∵OH⊥NP，
∴OH⊥MQ，
∴四边形EFQP为矩形，
∴EF=PQ=2米，
∴HF=OH−OE−EF=10−5−2=3(米)，即点H到线段MQ的距离为3米；
②此木箱能通过该桥洞，理由如下：
由②可知，若该箱子随水面上升1米，则此时点H到线段MQ的距离为2米，
当木箱的顶端MQ刚好通过该桥洞时，如图，连接OM，
则MF=QF=5米，ON=10米，
∴OF= OM2−MF2= 102−52=5 3(米)，
∴HF=(10−5 3)米，
∵10−5 3<2，
∴此木箱能通过该桥洞．
【解析】(1)易得OA=OB=OD=10米，由垂径定理可知CE=DE，由特殊角的三角函数值得∠ODE=30∘，于是DE=OD⋅cs∠ODE=5 3(米)，则CD=2DE.
(2)①延长OE交MQ于点F，交半圆O于点H，则点H为半圆O的最高点，OH=10米，易得OE=5米，OH⊥MQ，EF=PQ=2米，则点H到线段MQ的距离HF=OH−OE−EF；
②当箱子随水面上升1米，点H到线段MQ的距离为2米，求出当木箱刚好通过该桥洞时，HF的长度，若该长度小于2，则此木箱能通过该桥洞，否则不能．
本题主要考查垂径定理、勾股定理、特殊角的三角函数值、含30度角的直角三角形性质、矩形的判定与性质，熟练掌握垂径定理是解题关键．
25.【答案】解：(1)∵直线l：y=kx+b中，当x=−1时，y=−2；当x=0时，y=1，
∴−k+b=−2b=1，
解得k=3b=1，
∴直线l的解析式为y=3x+1；
(2)依题意可得直线l′的解析式为y=x+3，
画出直线l′如图：
(3)把x=a代入y=3x+1得，y=3a+1；
把x=a代入y=x+3得，y=a+3，
∵MN=3，
∴|3a+1−a−3|=3，
解得a=52或−12，
故答案为：52或−12；
(4)把y=m代入y=3x+1得，m=3x+1，解得x=m−13；
把y=m代入y=x+3得，m=x+3，解得x=m−3；
分三种情况：①当第三点在y轴上时，m−3+m−13=0，
解得m=52；
②当第三点在直线l上时，2×m−13=m−3，
解得m=7；
③当第三点在直线l′上时，2×(m−3)=m−13，
解得m=175；
∴直线y=m与直线l，l′及y轴有三个不同的交点，且其中两点关于第三点对称，则m的值为52或7或175，
故答案为：52或7或175.
【解析】(1)根据待定系数法求得即可；
(2)根据k、b的值，直接得到直线l′的表达式；
(3)求得两条直线与直线x=m的交点纵坐标，根据题意得到|3a+1−a−3|=3，解得即可；
(4)求得两条直线与直线y=m的交点横坐标，分三种情况讨论求得即可．
本题考查了一次函数图象与几何变换，两直线相交问题，待定系数法求一次函数的解析式，分类讨论是解题的关键．
26.【答案】解：(1)∵∠ACB=90∘，AB=10，csA=45，
∴AC=8，
∵∠ACB=90∘，△ABC绕点B顺时针旋转得到△A′BC′，
∴A′C=AC=8，
∵点A′落在AC的延长线上，
∴AA′=AC+A′C=16；
(2)过C作CF⊥AB于F，过M作MN⊥C′B于N，如图2：
∵∠ACB=90∘，AB=10，AC=8，
∴BC=6，
∵△ABC绕点B顺时针旋转得到△A′BC′，
∴∠A′BC=∠ABC，BC′=BC=6，
∵CF⊥AB，
∴Rt△ABC中，S△ABC=12AC⋅BC=12AB⋅CF，
∴CF=AC⋅BCAB=4.8，
Rt△CBF中，FB= CB2−CF2= 62−4.82=3.6，
∴C′F=FB+BC′=9.6，
由旋转性质可得：∠A′C′B=90∘，∠A′=∠A，
∵MN⊥AC′，∠A′C′B=90∘，
∴A′C′//MN，
∴∠BMN=∠A′，
∴cs∠BMN=csA=45，
∴MNBM=45，
∴NM=45MB，BN=35BM，
∴C′N=6−35BM，
∵△C′MN∽△C′CF，
∴C′NC′F=MNCF，
即6−35BM9.6=45BM4.8，
∴BM=3011；
(3)DE存在最大值4，理由如下：
过A作AP//A′C′交C′C于P，连接A′C，如图：
∵△ABC绕点B顺时针旋转得到△A′BC′，
∴BC=BC′，∠ACB=∠A′C′B=90∘，AC=A′C′，
∴∠BCC′=∠BC′C，
∴∠APC=180∘−∠APD，∠ACP=90∘−∠BCC′=90∘−∠BC′C=180∘−∠A′C′D，
∵AP//A′C′，
∴∠APD=∠A′C′D，
∴∠APC=∠ACP，
∴AP=AC，
∴AP=A′C′，
在△APD和△A′C′D中，
∠P=∠A′C′D∠PDA=∠A′DC′AP=A′C′，
∴△APD≌△A′C′D(AAS)，
∴AD=A′D，即D是AA′中点，
∵点E为AC的中点，
∴DE是△AA′C的中位线，
∴DE=12A′C.
当A′C的值最大时，DE的值最大，
∵A′C≤BC+BA′=8，
∴当C，B，A′三点共线时，DE存在最大值．
∴DE=12×8=4，
即DE的最大值为4.
【解析】(1)先利用余弦求出AC=8，再利用旋转对称得到A′C=AC=8，进而可得AA′=16；
(2)过C作CF⊥AB于F，过C作CD⊥AB于D，过M作MN⊥C′B于N，利用勾股定理得到BC=6，利用等面积法得到CF=AC⋅BCAB=4.8，再利用勾股定理求得FB=3.6，于是C′F=FB+BC′=9.6，利用cs∠BMN=csA=45，得到NM=45MB，BN=35BM以及C′N=6−35BM，最后利用△C′MN∽△C′CF得出C′NC′F=MNCF，即6−35BM9.6=45BM4.8，从而得解；
(3)过A作AP//A′C′交C′C于P，连接A′C，证明△APD≌△A′C′D(AAS)，由全等三角形的性质得出AD=A′D，由三角形中位线定理可得出DE=12A′C.要使DE最大，只需A′C最大，此时C，B，A′三点共线，A′C的最大值为A′B+BC=AB+BC，进一步解答则可求出答案．
本题考查直角三角形的旋转变换，涉及勾股定理、平行线分线段成比例、等腰三角形判定、全等三角形判定与性质等知识，综合性较强，解题的关键是作辅助线，构造全等三角形．分别以点A，C为圆心，以大于12AC长为半径作弧，两弧相交于点E，F，作直线EF，直线EF交AC于点O；
作射线BO，在BO上截取OD，使得OD=OB；
连接AD，CD，则四边形ABCD就是所求作的矩形.
x
结果代数式
2
n
2x+1
5
b
x2+2x
a
−1
胜一场
平一场
负一场
积分
3
1
0
奖金
(元/人)
1500
700
0
x
−1
0
y
−2
1
x
−3
0
y
0
3