

湖北省武汉市湖北华宜寄宿学校2023-2024学年八年级下学期期中考试数学试卷
展开一、单选题(共10小题,每小题3分,共30分)
1.(3分)下列二次根式是最简二次根式的是( )
A.B.C.D.
2.(3分)下列各组数中,是勾股数的是( )
A.9,16,25B.1,1,C.1,,2D.8,15,17
3.(3分)在式子5,x=2,a,a+b,,m+n>0,中,属于代数式的有( )
A.3B.4C.5D.6
4.(3分)在下列给出的条件中,能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BCB.∠A=∠B,∠C=∠D
C.AD∥BC,AD=BCD.AB=AD,CD=BC
5.(3分)下列各命题的逆命题成立的是( )
A.菱形四条边相等
B.如果两个实数相等,那么它们的绝对值相等
C.等边三角形是锐角三角形
D.全等三角形的对应角相等
6.(3分)已知,那么a应满足什么条件( )
A.a>0B.a≥0C.a=0D.a任何实数
7.(3分)矩形和菱形都一定具有的性质是( )
A.对角线互相垂直B.对角线互相平分
C.对角线长度相等D.对角线平分一组对角
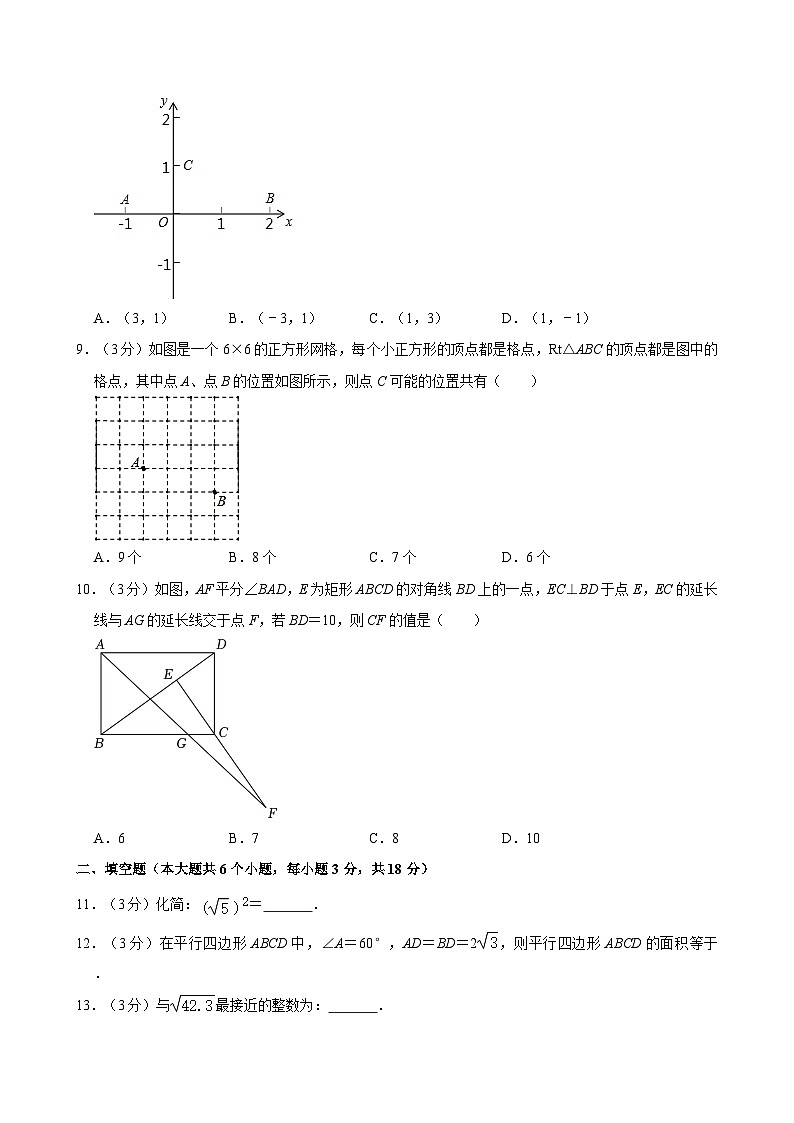
8.(3分)如图所示,平面直角坐标系中,已知三点A(﹣1,0),B(2,0),C(0,1),若以A、B、C、D为顶点的四边形是平行四边形,则D点的坐标不可能是( )
A.(3,1)B.(﹣3,1)C.(1,3)D.(1,﹣1)
9.(3分)如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )
A.9个B.8个C.7个D.6个
10.(3分)如图,AF平分∠BAD,E为矩形ABCD的对角线BD上的一点,EC⊥BD于点E,EC的延长线与AG的延长线交于点F,若BD=10,则CF的值是( )
A.6B.7C.8D.10
二、填空题(本大题共6个小题,每小题3分,共18分)
11.(3分)化简:= .
12.(3分)在平行四边形ABCD中,∠A=60°,AD=BD=2,则平行四边形ABCD的面积等于 .
13.(3分)与最接近的整数为: .
14.(3分)如图,四边形ABCD中,AB∥DC,∠A=90°,AB=AE=4,CD=DE=3.点F为BC的中点,则EF的长度为 .
15.(3分)2023年暑假,我校顺利完成了大门改造,新大门气势磅礴,宏伟壮观,彰显着非凡的尊贵气息.小蓝为了测量大门的高度AB,采取了以下方法:在校门口D点处测得大门顶A点处的仰角为45°,步行过马路后,马路宽度约为12米,在马路对面的F点处测得大门顶A点处的仰角为30°,已知小蓝的眼睛距离地面高度为CD=EF=1.6米,则大门高度AB约为 米.(仰角:是从低处向高处观察目标时,视线与水平线所形成的角度.结果保留2位小数,参考数据:≈1.732)
16.(3分)如图,在△ABC中,∠ABC=15°,∠ACB=37.5°,点D是边BC上的一点,且∠BAD=52.5°,S△ACD=3,则S△ABD= .
三、解答题(共8小题,共72分)
17.计算:
(1)2﹣6+3;
(2)(+3)(﹣5).
18.已知a=2+,b=2﹣,求值:a2+b2.
19.如图,将▱ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF.求证:四边形AECF是平行四边形.
20.如图是由边长为1的小正方形构成的8×8格,每个小正方形的点叫做格点.四边形ABDC的顶点是格点,点M是边AB与格线的交点,仅用无刻度的直尺在给定网格中按步骤完成下列画图,画图过程用虚线表示,画图结果用实线表示.
(1)过点C画线段CE,使CE∥AB,且CE=AB;
(2)在边AB上画一点F,使直线DF平分四边形ABEC的面积;
(3)过点M画线段MN,使MN∥CD,且MN=CD.
21.把一张长方形的纸片ABCD沿对角线BD折叠,折叠后,边BC的对应边BE交AD于F.
(1)求证:BF=DF;(长方形各内角均为90°)
(2)若AB=6,BC=8.求DF的长.
22.如图,在△ABC中,∠C=90°,∠BAC,∠ABC的角平分线交于点G,GE⊥BC于点E,GF⊥AC于点F.
(1)求证:四边形GECF是正方形;
(2)若AC=4,BC=3,求四边形GECF的面积.
23.(1)问题背景:小刚遇到一个这样问题:如图1,两条相等的线段AB,CD交于点O,∠AOC=60°,连接AC,BD,求证:AC+BD≥CD.通过尝试他发现通过平移可以解决这个问题.
证明:过点C作AB∥CE且使AB=CE,连接BE,
∴四边形ABEC为平行四边形,则AC= ,
∵AB∥CE、
∴∠DCE=∠ =60°,
又∵CD=AB=CE,
∴△DCE为等边三角形,
∴CD= ,
∴AC+BD=BE+BD≥DE=CD,即AC+BD≥CD.
请完成证明中的三个填空.并参考小刚同学思考的方法,解决下列问题:
(2)类比运用:如图2,AB与CD相交于点O,AC=3,BD=4,AB=5,∠AOC=30°,∠ACD+∠ABD=240°,求线段CD的长;
(3)联系拓展:如图3,△ABC的三条中线分别为AD,BE,CF.三条中线的交点为G.若△BDG的面积为3,则以AD,BE,CF的长度为三边长的三角形的面积等于 (请直接写出答案).
24.在平面直角坐标系中,四边形OABC为矩形,A(a,0),C(0,c),且.点E从B点出发沿BC运动,点F从B点出发沿BA运动,点G从O点出发沿OC运动.
(1)如图1,将△AOF沿OF折叠,点A恰好落在点E处,则E点的坐标为 ,F点的坐标为 ;
(2)如图2,若E,F两点以相同的速度同时出发运动,使∠EOF=45°,求OC+CE的值;
(3)如图3,已知点D为AO的中点,若F,G两点以相同的速度同时出发运动,连接FG,作AH⊥FG于H,直接写出DH的最大值.
参考答案与试题解析
一、单选题(共10小题,每小题3分,共30分)
1.(3分)下列二次根式是最简二次根式的是( )
A.B.C.D.
【解答】解:(A)原式=2,故A不选;
(C)原式=2,故C不选;
(D)原式=,故D不选;
故选:B.
2.(3分)下列各组数中,是勾股数的是( )
A.9,16,25B.1,1,C.1,,2D.8,15,17
【解答】解:A、92+162≠252,不是勾股数,故此选项不合题意;
B、不是正整数,不是勾股数,故此选项不合题意;
C、不是正整数,不是勾股数,故此选项不合题意;
D、82+152=172,都是正整数,是勾股数,故此选项符合题意;
故选:D.
3.(3分)在式子5,x=2,a,a+b,,m+n>0,中,属于代数式的有( )
A.3B.4C.5D.6
【解答】解:在式子5,x=2,a,a+b,,m+n>0,中,属于代数式的有5,a,a+b,,共4个,
故选:B.
4.(3分)在下列给出的条件中,能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BCB.∠A=∠B,∠C=∠D
C.AD∥BC,AD=BCD.AB=AD,CD=BC
【解答】解:A、由AB∥CD,AD=BC,不能判定四边形ABCD为平行四边形,故选项A不符合题意;
B、由∠A=∠B,∠C=∠D,不能判定四边形ABCD为平行四边形,故选项B不符合题意;
C、∵AD∥BC,AD=BC,
∴四边形ABCD是平行四边形,故选项C符合题意;
D、AB=AD,CB=CD,由不能判定四边形ABCD为平行四边形,故选项D不符合题意;
故选:C.
5.(3分)下列各命题的逆命题成立的是( )
A.菱形四条边相等
B.如果两个实数相等,那么它们的绝对值相等
C.等边三角形是锐角三角形
D.全等三角形的对应角相等
【解答】解:A、逆命题为:四条边相等的四边形是菱形,成立,符合题意;
B、逆命题为:如果两个实数的绝对值相等,那么这两个实数也相等,不成立,不符合题意;
C、逆命题为:锐角三角形是等边三角形,不成立,不符合题意;
D、逆命题为:对应角相等的三角形全等,不成立,不符合题意.
故选:A.
6.(3分)已知,那么a应满足什么条件( )
A.a>0B.a≥0C.a=0D.a任何实数
【解答】解:∵()2=a≥0且a≥0,=|a|≥0,
∴|a|=a,
∴a≥0.
故选:B.
7.(3分)矩形和菱形都一定具有的性质是( )
A.对角线互相垂直B.对角线互相平分
C.对角线长度相等D.对角线平分一组对角
【解答】解:矩形的性质是:①矩形的四个角度数直角,②矩形的对边相等且互相平行,③矩形对角线相等且互相平分;
菱形的性质是:①菱形的四条边都相等,菱形的对边互相平行;②菱形的对角相等,③菱形的对角线互相平分且垂直,并且每条对角线平分一组对角,
所以矩形和菱形都具有的性质是对角线互相平分,
故选:B.
8.(3分)如图所示,平面直角坐标系中,已知三点A(﹣1,0),B(2,0),C(0,1),若以A、B、C、D为顶点的四边形是平行四边形,则D点的坐标不可能是( )
A.(3,1)B.(﹣3,1)C.(1,3)D.(1,﹣1)
【解答】解:当以BC为对角线时:CD=AB=3,此时D(3,1);
当以AC为对角线时,CD=AB=3,此时(﹣3,1);
当以AB为对角线时,AD=BC==,此时点D(1,﹣1).
∴D点的坐标不可能是:(1,3).
故选:C.
9.(3分)如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )
A.9个B.8个C.7个D.6个
【解答】解:如图:
符合条件的点C一共有9个.
故选:A.
10.(3分)如图,AF平分∠BAD,E为矩形ABCD的对角线BD上的一点,EC⊥BD于点E,EC的延长线与AG的延长线交于点F,若BD=10,则CF的值是( )
A.6B.7C.8D.10
【解答】解:过A作AH⊥BD于H,连接AC,
∵AF平分∠BAD,
∴∠BAG=∠DAG
∵四边形ABCD是矩形,
∴AC=BD=10,∠BAD=90°,OA=OD,
∴∠BAH+∠DAH=∠ADB+∠DAH=90°,
∴∠BAH=∠ADH,
∵OA=OD,
∴∠ADH=∠DAC,
∴∠BAH=DAC,
∴∠BAG﹣∠BAH=∠DAG﹣∠DAC,
∴∠GAH=∠CAH,
∵EC⊥BD,AH⊥BD,
∴AH∥CE,
∴∠F=∠GAH,
∴∠F=∠CAH,
∴CF=AC=10.
故选:D.
二、填空题(本大题共6个小题,每小题3分,共18分)
11.(3分)化简:= 5 .
【解答】解:=5.
故答案为:5.
12.(3分)在平行四边形ABCD中,∠A=60°,AD=BD=2,则平行四边形ABCD的面积等于 6 .
【解答】解:如图,过点B作BE⊥AD于点E.
∵AD=DB=2,∠A=60°,
∴△ABD是等边三角形,
∴AB=BD=2,
∵BE⊥AD,
∴AE=ED=,
∴BE===3,
∴平行四边形ABCD的面积=2×3=6.
故答案为:6.
13.(3分)与最接近的整数为: 7 .
【解答】解:∵=6.5,=7,
且<<,
∴6.5<<7,
∴与最接近的整数为7,
故答案为:7.
14.(3分)如图,四边形ABCD中,AB∥DC,∠A=90°,AB=AE=4,CD=DE=3.点F为BC的中点,则EF的长度为 .
【解答】解:连接DF并延长交AB的延长线于H,过点C作CM⊥AB于M,如下图所示:
∵AB∥DC,∠DAB=90°,AB=AE=4,CD=DE=3,
∴四边形ADCM为矩形,
∴CM=AD=AE+DE=7,AM=CD=3,
∴BM=AB﹣AM=4﹣3=1,
在Rt△CMB中,由勾股定理得:BC===,
∵点F为BC的中点,
∴CF=BF=BC=,
∵DC∥AB,
∴∠1=∠H,∠DCF=∠HBF,
在△DCF和△HBF中,
∠1=∠H,∠DCF=∠HBF,CF=BF,
∴△DCF≌△HBF(AAS),
∴CD=BH=3,DF=HF,
∴AH=AB+BH=4+3=7,
∴AD=AH,
∴∠2=∠H,
∴∠1=∠2,
在△DCF和△DEF中,
CD=DE,∠1=∠2,DF=DF,
∴△DCF≌△DEF(SAS),
∴EF=CF=.
故答案为:.
15.(3分)2023年暑假,我校顺利完成了大门改造,新大门气势磅礴,宏伟壮观,彰显着非凡的尊贵气息.小蓝为了测量大门的高度AB,采取了以下方法:在校门口D点处测得大门顶A点处的仰角为45°,步行过马路后,马路宽度约为12米,在马路对面的F点处测得大门顶A点处的仰角为30°,已知小蓝的眼睛距离地面高度为CD=EF=1.6米,则大门高度AB约为 7.06 米.(仰角:是从低处向高处观察目标时,视线与水平线所形成的角度.结果保留2位小数,参考数据:≈1.732)
【解答】解:在Rt△ADG中,
∵∠ADG=45°,
∴∠DAG=45°=∠ADG,
∴AG=DG,
在Rt△AEG中,∠AEG=30°,GE=DG+DE=12+AG,tan∠AEG=,
∴AG=GE•tan30°,
∴AG=(12+AG)
解得AG≈5.46(米),
由题意知四边形BFEG是矩形,
∴BG=EF=1.6米,
∴AB=AG+BG=5.46+1.6=7.06(米).
答:大门高度AB约为7.06米.
故答案为:7.06.
16.(3分)如图,在△ABC中,∠ABC=15°,∠ACB=37.5°,点D是边BC上的一点,且∠BAD=52.5°,S△ACD=3,则S△ABD= .
【解答】解:以点A为圆心,AB为半径画弧交BC的延长线于E,连接AE,则AB=AE,把△ABD绕点A逆时针旋转150°得到△AEF,连接CF,过点C作CH⊥EF于H,设CH=a,如下图所示:
由旋转的性质可知:∠DAF=150°,∠AEF=∠B=15°,BD=EF,AD=AF,
在△ABE中,AB=AE,
∴∠AEB=∠B=15°,
∴∠CEF=∠AEB+∠AEF=30°,
在△ABC中,∠B=15°,∠ACB=37.5°,
∴∠BAC=180°﹣(∠B+∠ACB)=180°﹣(15°+37.5°)=127.5°,
又∵∠BAD=52.5°,
∴∠DAC=∠BAC﹣∠BAD=127.5°﹣52.5°=75°,
∴∠FAC=∠DAF﹣∠DAC=150°﹣75°=75°,
即∠DAC=∠FAC,
在△DAC和△FAC中,
,
∴△DAC≌△FAC(SAS),
∴∠DCA=∠FCA=37.5°,CD=CF,
即∠DAF=∠DCA+∠FCA=75°,
∴∠FCE=180°﹣∠DAF=180°﹣75°=105°,
在Rt△CEH中,∠CEF=30°,CH=a,
∴∠HCE=60°,CE=2CH=2a,
由勾股定理得:EH==,
∴∠FCH=∠FCE﹣∠HCE=105°﹣60°=45°,
∴△FCH为等腰直角三角形,即FH=CH=a,
由勾股定理得:CF==,
∴CD=CF=,BD=EF=EH+FH==,
∴=,
∵△ABD的边BD和△ACD的边CD上的高相同,
∴得=,
又∵S△ACD=,
∴S△ABD==.
故答案为:.
三、解答题(共8小题,共72分)
17.计算:
(1)2﹣6+3;
(2)(+3)(﹣5).
【解答】解:(1)原式=4﹣2+12
=14;
(2)原式=2﹣5+3﹣15
=﹣13﹣2.
18.已知a=2+,b=2﹣,求值:a2+b2.
【解答】解:∵a=2+,b=2﹣,
∴a+b=4,ab=1,
∴a2+b2=(a+b)2﹣2ab=42﹣2×1=14.
19.如图,将▱ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF.求证:四边形AECF是平行四边形.
【解答】证明:连接AC,设AC与BD交于点O.如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵BE=DF,
∴OE=OF.
∴四边形AECF是平行四边形.
20.如图是由边长为1的小正方形构成的8×8格,每个小正方形的点叫做格点.四边形ABDC的顶点是格点,点M是边AB与格线的交点,仅用无刻度的直尺在给定网格中按步骤完成下列画图,画图过程用虚线表示,画图结果用实线表示.
(1)过点C画线段CE,使CE∥AB,且CE=AB;
(2)在边AB上画一点F,使直线DF平分四边形ABEC的面积;
(3)过点M画线段MN,使MN∥CD,且MN=CD.
【解答】解:(1)如图,线段CE即为所求.
(2)如图,直线DF即为所求.
(3)如图,线段MN即为所求.
21.把一张长方形的纸片ABCD沿对角线BD折叠,折叠后,边BC的对应边BE交AD于F.
(1)求证:BF=DF;(长方形各内角均为90°)
(2)若AB=6,BC=8.求DF的长.
【解答】(1)证明:由折叠的性质知,CD=ED,BE=BC.
∵四边形ABCD是矩形,
在△ABF和△EDF中,
,
∴△ABF≌△EDF(AAS),
∴BF=DF;
(2)解:∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=8,
∴,
由(1)知BF=DF,
∴AF=8﹣DF=8﹣BF,
∵AB2+AF2=BF2,
∴62+(8﹣BF)2=BF2,
∴,
22.如图,在△ABC中,∠C=90°,∠BAC,∠ABC的角平分线交于点G,GE⊥BC于点E,GF⊥AC于点F.
(1)求证:四边形GECF是正方形;
(2)若AC=4,BC=3,求四边形GECF的面积.
【解答】(1)证明:过G作GD⊥AB于D,
∵∠CAB、∠CBA的角平分线交于G点,GE⊥BC于点E,GF⊥AC于点F,
∴DG=EG,DG=FG,
∴EG=FG,
∵△ABC是直角三角形,∠C=90°,GE⊥BC,GF⊥AC,
∴∠C=∠CEG=∠CFG=90°,
∴四边形GECF是矩形,
∵EG=FG,
∴四边形GECF为正方形;
(2)解:如图2,连接CG,过G作GD⊥AB于D,
由勾股定理得:AB==5,
设EG=x,则DG=FG=x,
∵S△ABC=S△AGB+S△AGC+S△BCG,
∴×3×4=•5x+•4x+•3x,
∴x=1,
∴四边形GECF的面积=EG2=1.
23.(1)问题背景:小刚遇到一个这样问题:如图1,两条相等的线段AB,CD交于点O,∠AOC=60°,连接AC,BD,求证:AC+BD≥CD.通过尝试他发现通过平移可以解决这个问题.
证明:过点C作AB∥CE且使AB=CE,连接BE,
∴四边形ABEC为平行四边形,则AC= BE ,
∵AB∥CE、
∴∠DCE=∠ AOC =60°,
又∵CD=AB=CE,
∴△DCE为等边三角形,
∴CD= DE ,
∴AC+BD=BE+BD≥DE=CD,即AC+BD≥CD.
请完成证明中的三个填空.并参考小刚同学思考的方法,解决下列问题:
(2)类比运用:如图2,AB与CD相交于点O,AC=3,BD=4,AB=5,∠AOC=30°,∠ACD+∠ABD=240°,求线段CD的长;
(3)联系拓展:如图3,△ABC的三条中线分别为AD,BE,CF.三条中线的交点为G.若△BDG的面积为3,则以AD,BE,CF的长度为三边长的三角形的面积等于 (请直接写出答案).
【解答】(1)证明:过点C作AB∥CE且使AB=CE.连接BE.
∴四边形ABEC为平行四边形,则AC=BE.
∵AB∥CE,
∴∠DCE=∠AOC=60°.
又∵CD=AB=CE,
∴△DCE为等边三角形,
∴CD=DE.
∴AC+BD=BE+BD≥DE=CD,即AC+BD≥CD.
故答案为:BE、AOC、DE;
(2)解:过A作AF∥CD,过D作DF∥AC,两直线交于F,连接BF,
则四边形AFDC是平行四边形,
所以∠FAB=∠AOC=30°,∠C=∠AFD,AC=DF=3,
∵∠ABD+∠C=240°,
∴∠ABD+∠DFA=240°,
∴∠FDB=360°﹣240°﹣30°=90°,
∴△FDB是直角三角形,
∵DF=3,BD=4,
∴由勾股定理得:FB=5,
∴AB=FB,
∴∠BAF=∠AFB=45°,
∴∠ABF=90°,
∴由勾股定理得:AF=5,
∵四边形AFDC是平行四边形,
∴CD=AF=5.
(3)解:平移AF到PE,可得AF∥PE,AF=PE,
∴四边形AFEP为平行四边形,
∴AE与PF互相平分,即M为PF的中点,
又∵AP∥FN∥BC,F为AB的中点,
∴N为PC的中点,
∴E为△PFC各边中线的交点,
∴△PEC的面积为△PFC面积的,
连接DE,可知DE与PE在一条直线上,
∴△EDC的面积是△ABC面积的,
∴S△PFC=3S△CFE=3S△EDC=,
∵△BDG的面积为3,
∴S△ABG=2S△BDG=6,
∴S△ABC=2S△ABD=18,
所以△PFC的面积是18×=,
∴以AD、BE、CF的长度为三边长的三角形的面积等于,
故答案为:.
24.在平面直角坐标系中,四边形OABC为矩形,A(a,0),C(0,c),且.点E从B点出发沿BC运动,点F从B点出发沿BA运动,点G从O点出发沿OC运动.
(1)如图1,将△AOF沿OF折叠,点A恰好落在点E处,则E点的坐标为 (6,8) ,F点的坐标为 (10,5) ;
(2)如图2,若E,F两点以相同的速度同时出发运动,使∠EOF=45°,求OC+CE的值;
(3)如图3,已知点D为AO的中点,若F,G两点以相同的速度同时出发运动,连接FG,作AH⊥FG于H,直接写出DH的最大值.
【解答】解:(1)∵,≥0,(c﹣8)2≥0,
∴10﹣a=0,c﹣8=0,
∴a=10,c=8.
∴A(10,0),C(0,8).
∴OA=10,OC=8.
∵四边形OABC为矩形,
∴AB=OC=8,BC=OA=10.
∵将△AOF沿OF折叠,点A恰好落在点E处,
∴EF=FA,OE=OA=4,
∴CE==6,
∴E(6,8);
∴BE=BC﹣CE=4,
设EF=FA=x,则BF=8﹣x,
∵BE2+BF2=EF2,
∴42+(8﹣x)2=x2,
∴x=5.
∴AF=5.
∴F(10,5).
故答案为:(6,8);(10,5);
(2)延长EF交x轴于点G,延长FE交y轴于点D,过点O作OH⊥OF,使OH=OF,连接EH,HD,如图,
∵OH⊥OF,∠EOF=45°,
∴∠HOE=∠FOE=45°.
在△OEH和△OEF中,
,
∴△OEH≌△OEF(SAS),
∴HE=EF.
∵∠HOF=∠COA=90°,
∴∠HOD=∠FOG.
∵E,F两点以相同的速度同时出发运动,
∴BE=BF,
∴△BEF为等腰直角三角形,
∴∠BEF=∠BFE=45°,
∴∠DEC=∠BEF=∠AFG=∠BFE=45°,
∴△CED和△AFG为等腰直角三角形,
∴DC=CE,AF=AG,∠AGF=∠ADE=45°,
∴DE2=2CE2,FG2=2AF2,△ODG为等腰直角三角形,
∴OD=OG.
在△ODH和△OGF中,
,
∴△ODH≌△OGF(SAS),
∴DH=FG,∠HDO=∠FGA=45°,
∴∠HDE=∠HDO+∠CDE=45°+45°=90°,DH2=2AF2,
∴DH2+DE2=EF2.
∴2AF2+2CE2=2BE2,
∴AF2+CE2=BE2,
设CE=m,则BE=BF=10﹣m,
∴AF=AB﹣BF=m﹣2,
∴(m﹣2)2+m2=(10﹣m)2,
∴m2+16m﹣96=0.
∴m=﹣8(负数不合题意,舍去),
∴CE=4﹣8,
∴OC+CE=8+4﹣8=4.
(3)连接OB,交GF于点K,连接KD,AK,取AK的中点M,连接MD,MH,如图,
∵F,G两点以相同的速度同时出发运动,
∴OG=BF.
∵OG∥AB,
∴∠KGO=∠KFB.
在△OGK和△BFK中,
,
∴△OGK≌△BFK(AAS),
∴KO=KB,
即点K为矩形OABC的中心,
∴AK=OK=BK=BO===,
∵点D为AO的中点,M为AK的中点,
∴DM=OK=.
∵AH⊥FG,M为AK的中点,
∴MH=AK=.
∵DH≤DM+NH,
∴当点D,M,H三点在一条直线上时,DH取得最大值=DM+NH,
∴DH的最大值为.
湖北省武汉市华一寄宿中学2022-2023学年上学期期末八年级数学试卷: 这是一份湖北省武汉市华一寄宿中学2022-2023学年上学期期末八年级数学试卷,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
湖北省武汉市华宜寄宿学校2023-2024学年八年级上学期月考数学试题(无答案): 这是一份湖北省武汉市华宜寄宿学校2023-2024学年八年级上学期月考数学试题(无答案),共5页。试卷主要包含了已知,如图,,则的度数为等内容,欢迎下载使用。
湖北省武汉市华一寄宿中学2022—2023学年上学期期末八年级数学试卷: 这是一份湖北省武汉市华一寄宿中学2022—2023学年上学期期末八年级数学试卷,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












