【大单元教学】鲁教版数学八年级下册 《 图形的相似》单元整体设计 课件

这是一份【大单元教学】鲁教版数学八年级下册 《 图形的相似》单元整体设计 课件，共24页。

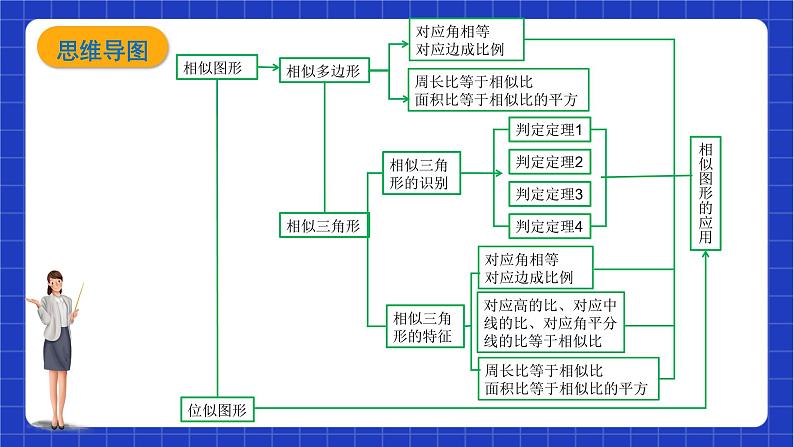
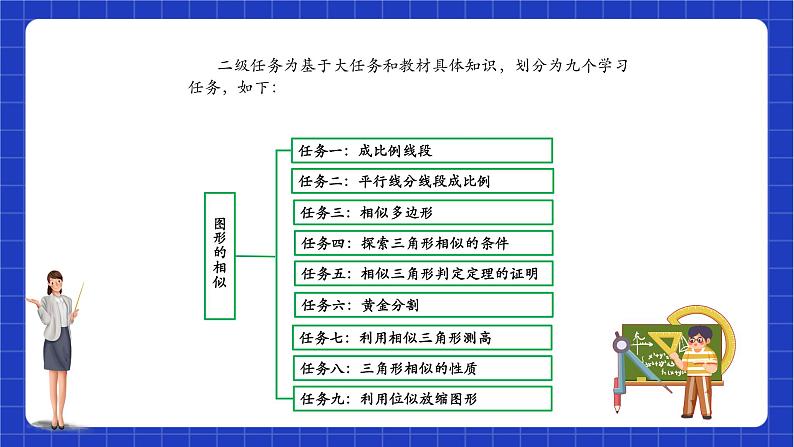
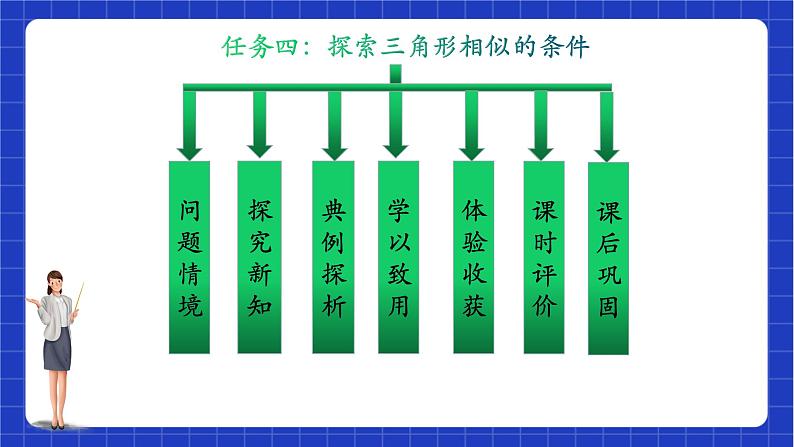
图形的相似 单元整体设计 鲁教版数学八年级下册1、了解比例的基本性质、线段的比、成比例的线段；通过建筑、艺术上的实例了解黄金分割。2、通过具体实例认识图形的相似。了解相似多边形和相似比。3、掌握基本事实：两条直线被一组平行线所截，所得的对应线段成比例。4、了解相似三角形的判定定理：两角分别相等的两个三角形相似；两边成比例且夹角相等的两个三角形相似；三边成比例的两个三角形相似。*了解相似三角形判定定理的证明。5、了解相似三角形的性质定理：相似三角形对应线段的比等于相似比；面积比等于相似比的平方。6、了解图形的位似，知道利用位似可以将一个图形放大或缩小。7、会利用图形的相似解决一些简单的实际问题。课标要求1、在研究与图形相似有关的问题中，经历观察、操作、类比、归纳、交流等过程，进一步发展几何直观、空间观念和推理能力，发展发现问题、提出问题、解决问题的能力，积累数学活动经验。2、了解线段的比、成比例线段，掌握比例的性质及平行线分线段成比例的基本事实。3、了解相似多边形和相似比。4、探索并了解三角形相似的条件和性质。5、了解相似三角形判定定理的证明。6、了解图形的位似，能够利用位似将一个图形放大或缩小。7、探索并了解多边形的顶点坐标（有一个顶点为原点、有一条边在横坐标轴上）分别扩大或缩小相同倍数时所对应的图形与原图形的位似关系。8、了解黄金分割，了解相似图形在现实生活中的应用；在探索问题、合作交流过程中，进一步体会数学与自然及人类社会的密切联系和数学的价值，增强应用意识。教学目标思维导图 一级任务是整个单元的打任务：学生在七年级上学期学习了证明探索三角形全等的条件的基础，类比学习三角形相似的判定条件。总体教学思路是 开始学习线段的比和成比例线段内容时，就以“形”为载体，努力克服就“数”论“数”的局限，既有利于学生通过“形”的直观感知，加深对“数”认识，又进一步渗透了“数”与“形”相结合的数学思想。同时，在呈现作为知识与技能的数学结果的同时，重视学生已有的经验，使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程”的要求。任务划分 二级任务为基于大任务和教材具体知识，划分为九个学习任务，如下：课时分配：1、成比例线段 2 课时2、平行线分线段成比例 1课时3、相似多边形 1课时4、探索三角形相似的条件 3课时5、相似三角形判定定理的证明 1课时6、黄金分割 1课时7、利用相似三角形测高 1课时 8、三角形相似的性质 2课时9、利用位似放缩图形 2课时 二级任务为基于大任务和教材具体知识，划分为九个学习任务，课时分配如下：任务四：探索三角形相似的条件课后巩固类比思考:相似三角形的判定方法能够完全重合的两个三角形对应角相等，对应边相等三角对应相等，三边对应成比例对应角相等，对应边成比例SSS,SAS,ASA,AAS猜一猜：判断三角形相似需要几个条件？问题情境 角 ｛+角+边 边｛→ 两个角相等小明和小亮在老师的指导下分别制作了两个风筝（如图所示）这两个风筝形状有何关系？如何证明这两个三角形的风筝相似呢？探究新知回答下面的问题：（1）∠C与∠F相等吗？（2）三边的比 相等吗？(测量精确到1mm) (3)这两个三角形相似吗？（计算结果精确到0.01）两个角对应相等的两个三角形相似 四人小组、合作探究： ·一个人画△ABC，使得∠A=45º，∠B=60°； ·另一个人画△DEF,使得∠D=45º，∠E=60°； ·第三人测量∠C与∠F、三角形各边的长； ·最后一人计算三组对应边的比。动手探究判定三角形相似的方法一：两角分别相等的两个三角形相似.∵∠A=∠D, ∠B=∠E,∴△ ABC∽ △DEF.在△ ABC和△ DEF中 ，探究归纳如图，D，E分别是△ABC边AB，AC上的点，DE∥BC.认识“A”字形（1）图中有哪些相等的角？（2）找出图中的相似三角形， 并说明理由；（3）写出三组成比例的线段。（4）若AB=7，AD=5，DE=10， 求BC的长.典例探析 2、 如图所示，∠1=∠2，（1）请找出图中的相似三角形（2）你能说出图中所有的对应边、对应角吗？1、判断题：（1）有一个锐角相等的两个直角三角形相似. （2）有一个角为110º的两个等腰三角形相似。( )( )学以致用已知：Rt△ABC中， ∠BAC=90º,AD⊥BC,试找出图中有哪几对相似三角形？思考：你能得出认识“双垂直”拓展提升体验收获 1、如图所示，∠1=∠2，则（1）△ ∽ △ . 认识“斜A”形（2）请找出图中另一组相等的角。 2、如图，AB∥CD，AD与BC相交于点O，那么在下列比例式中，正确的是（ ） C认识“X”字形课时评价3、如图，已知点D,E分别在AB,AC或它们的延长线上，且∠1=∠2,分别指出图中的相似三角形。必做：课本习题P100 1-4选做：5课后巩固相似三角形基本图形单元评价1、在平行四边形ABCD中,AE:BE=1:2.若S△AEF=6cm2,则S△CDF = cm2 2、如图， △ABC中，DE⁄⁄FG⁄⁄BC，AD＝DF＝FB，则Ｓ△ＡＤＥ:Ｓ四边形ＤＦＧＥ:Ｓ四边形ＦＢＣＧ=_______3、如图所示，E是正方形ABCD的边AB上的动点， EF⊥DE交BC于点F．求证: △ADE∽△BEF；单元评价5、如图，AE2＝AD·AB，且∠ABE＝∠BCE，试说明△EBC∽△DEB课程结束