【大单元教学】鲁教版数学八年级下册《图形的相似》 课件

这是一份【大单元教学】鲁教版数学八年级下册《图形的相似》 课件，共52页。

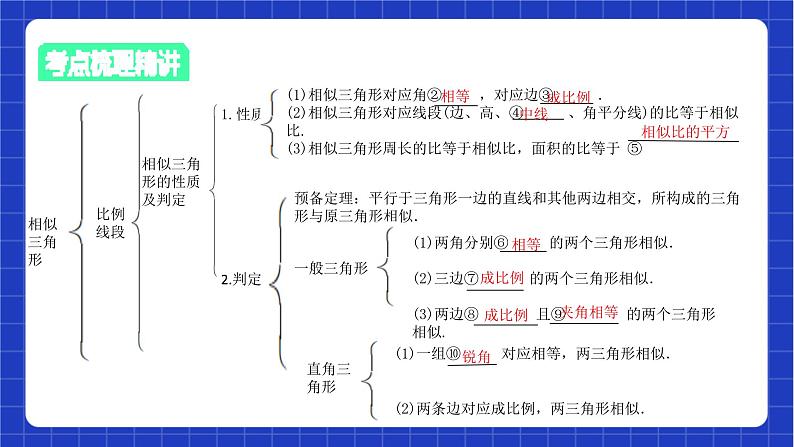
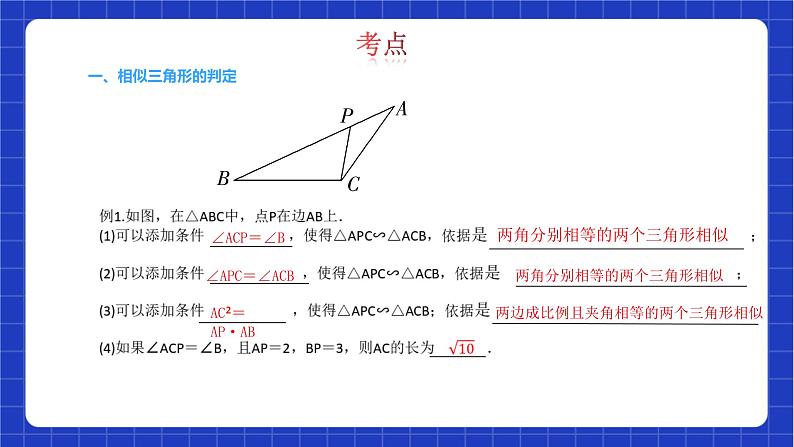
图形的相似 鲁教版数学八年级下册1.了解比例的基本性质、线段的比、成比例的线段；通过建筑、艺术上的实例了解黄金分割．2．掌握基本事实：两条直线被一组平行线所截，所得的对应线段成比例．3．了解相似三角形的性质定理和判定定理．4．通过具体实例认识图形的相似，了解相似多边形和相似比．5．会利用图形的相似解决一些简单的实际问题．6．了解相似三角形判定定理的证明．重难点相似三角形比例线段比例性质平行线分线段成比例   (abcd≠0)(1)基本事实：两条直线被一组平行线所截，所,得的线段成比例．如图1，图2，当l1∥l2∥,l3时, (2)推论：平行于三角形一边的直线截其他两边(或两边的延长,线)，所得的线段成比例．如图3，当DE∥BC时，有＝ad=bc相似三角形比例线段相似三角形的性质及判定1.性质2.判定(1)相似三角形对应角② ，对应边③ ．(2)相似三角形对应线段(边、高、④ 、角平分线)的比等于相似比.(3)相似三角形周长的比等于相似比，面积的比等于 ⑤ 预备定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似．一般三角形 (1)两角分别⑥ 的两个三角形相似．(2)三边⑦ 的两个三角形相似．(3)两边⑧ 且⑨ 的两个三角形相似.直角三角形(1)一组⑩ 对应相等，两三角形相似．(2)两条边对应成比例，两三角形相似．相等成比例中线相似比的平方 相等成比例成比例 夹角相等锐角 发 相似三角形相似多边形的性质及判定1.性质2.判定(1)对应角相等，对应边⑪ ．(2)对应边的比、周长的比都等于⑫ ，面积的比等于⑬ ．(1)对应角相等，对应边成比例的多边形是相似多边形．(2)所有对应边成比例，那么这两个多边形是相似多边形．相似三角形的实际运用1.步骤2.常考类型(1)将实际问题转化为相似三角形问题．(2)找出一对相似三角形．(3)根据相似三角形的性质，表示出相应的量，并求解． 成比例相似比相似比的平方相似三角形图形的位似定义 ：如果两个图形不仅是相似图形，而且每组对应点所在直线都经过同一点，那么这两个图,形叫做位似图形，这个点叫做位似中心2.性质3．位似变换与坐标的关系：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k,那么位似图形对应点的坐标等于k 或⑰ (1)位似图形上的任意一对对应点到位似中心的距离之比等于⑭ ，面积比等,于相似比的平方．(2)位似图形对应点的连线或延长线相交于同一点．(3)位似图形对应边⑮ 且成比例．(4)位似图形对应角⑯ ．相似比平行(或共线)相等-k一、相似三角形的判定 ∠ACP＝∠B两角分别相等的两个三角形相似∠APC＝∠ACB两角分别相等的两个三角形相似AC²＝AP·AB两边成比例且夹角相等的两个三角形相似 考点练习1.如图，在△ABC和△ADE中，∠BAD＝∠CAE，∠ABC＝∠ADE.图中相似三角形有 △ABC∽△ADE，△ABD∽△ACE.考点二、相似三角形的判定和性质例2.(2020·杭州中考)如图，在△ABC中，点D，E，F分别在AB，BC，AC边上，DE∥AC，EF∥AB.(1)求证：△BDE∽△EFC； ②若△EFC的面积是20，求△ABC的面积．考点 考点  考点练习3.如图，在△ABC中，BC＝120，高AD＝60，正方形EFGH一边在BC上，点E，F分别在AB，AC上，AD交EF于点N，求AN的长． 考点命题点 成比例的线段   B命题点   命题点2命题点 平行线分线段成比例C命题点  C命题点3命题点 相似三角形的性质与判定5．★如图，每个小正方形的边长均为1，则下列图形中的三角形(阴影部分)与△A1B1C1相似的是(　 )解析：因为△A1B1C1中有一个角是135°，选项中有135°角的三角形只有B，且满足两边成比例夹角相等．B命题点6．(2021·济南中考)如图，在△ABC中，∠ABC＝90°，∠C＝30°，以点A为圆心，以AB的长为半径作弧交AC于点D，连接BD，再分别以点B，D为圆心，大于 BD的长为半径作弧，两弧交于点P，作射线AP交BC于点E，连接DE，则下列结论中不正确的是( )A．BE＝DE B．DE垂直平分线段ACC． D．BD2＝BC·BEC命题点解析：∵△ABC与△DEF相似且面积之比为25∶16，∴△ABC与△DEF的相似比为5∶4，∴△ABC的中线AM与△DEF的中线DN之比为5∶4.5∶47．★若△ABC与△DEF相似且面积之比为25∶16，则△ABC的中线AM与△DEF的中线DN之比为 _________.命题点8．★(2021·菏泽中考)如图，在△ABC中，AD⊥BC，垂足为D，AD＝5，BC＝10，四边形EFGH和四边形HGNM均为正方形，且点E，F，G，N，M都在△ABC的边上，那么△AEM与四边形BCME的面积比为 . 1∶3命题点9．如图，点E是四边形ABCD的对角线BD上一点，且∠BAC＝∠BDC＝∠DAE.求证：△ABE∽△ACD.证明：∵∠BAC＝∠BDC，∠AOB＝∠DOC，∴∠ABE＝∠ACD.又∵∠BAC＝∠DAE，∴∠BAC＋∠EAC＝∠DAE＋∠EAC，∴∠EAB＝∠DAC，∴△ABE∽△ACD.命题点10．(2021·牡丹江中考)Rt△ABC中，∠C＝90°，AB＝17，BC＝8，矩形CDEF的另三个顶点D，E，F均在Rt△ABC的边上，且邻边之比为1∶2，画出符合题意的图形，并直接写出矩形周长的值．命题点命题点4命题点 相似三角形的应用 3命题点5命题点 位似图形的性质12．(2021·重庆中考)如图，在平面直角坐标系中，将△OAB以原点O为位似中心放大后得到△OCD，若B(0,1)，D(0,3)，则△OAB与△OCD的相似比是(　 )A．2∶1 B．1∶2 C．3∶1 D．1∶3解析：∵B(0,1)，D(0,3)，∴OB＝1，OD＝3.∵将△OAB以原点O为位似中心放大后得到△OCD，∴△OAB与△OCD的相似比是OB∶OD＝1∶3.D命题点13．(2021·东营中考)如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是(1,0)，以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍，设点B的横坐标是a，则点B的对应点B′的横坐标是( )A．－2a＋3 B．－2a＋1C．－2a＋2 D．－2a－2解析：设点B′的横坐标为x，则B，C间的横坐标的长度为a－1，B′，C间的横坐标的长度为－x＋1.∵△ABC放大到原来的2倍得到△A′B′C，∴2(a－1)＝－x＋1，解得x＝－2a＋3.A命题点14．★(2021·遂宁中考)如图，正方形ABCD中，点E是CD边上一点，连接BE，以BE为对角线作正方形BGEF，边EF与正方形ABCD的对角线BD相交于点H，连接AF，有以下五个结论：①∠ABF＝∠DBE；②△ABF∽△DBE；③AF⊥BD；④2BG2＝BH·BD；⑤若CE∶DE＝1∶3，则BH∶DH＝17∶16.你认为其中正确是_________.(填写序号)①②③④命题点素养提升  命题点模型 1“A”字型相似三角形模型1．如图1，在△ABC中，点D，E分别在AB，AC边上，且∠ABC＝∠ADE，则有△ADE∽△ABC.2．如图2，在△ABC中，点D，E分别在AB，AC边上，且∠ABC＝∠AED，则有△AED∽△ABC. 1．如图，在△ABC中，∠ADE＝∠B，AD＝7，AB＝10，DE＝6，∠A＝65°，∠B＝40°，求：(1)∠AED与∠C的度数；(2)BC的长．命题点2．如图，在△ABC中，AB＝8厘米，AC＝16厘米，点P从A出发，以每秒2厘米的速度向B运动，点Q从C同时出发，以每秒3厘米的速度向A运动，其中一个动点到端点时，另一个动点也相应停止运动，设运动的时间为t(秒)．(1)用含t的代数式表示：AP= 厘米，AQ＝ 厘米；(2)当以A，P，Q为顶点的三角形与△ABC相似时，运动时间是多少？ 2t 16-3t命题点2模型 “8”字型相似三角形模型1．如图3，在△ABC中，点D，E分别在BA，CA边的延长线上，且∠ABC＝∠ADE，则有△ADE∽△ABC.2．如图4，在△ABC中，点D，E分别在BA，CA边的延长线上，且∠ABC＝∠AED，则有△ADE∽△ACB.3．如图，BD，AC相交于点P，连接BC，AD，且∠1＝∠2，AD＝3，DP＝2，CP＝1，求BC的长． 4．如图，在四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点．求证：(1)AC²＝AB·AD；(2)△AFD∽△CFE.证明：(1)∵AC平分∠DAB，∴∠DAC＝∠CAB.又∵∠ADC＝∠ACB＝90°，∴△ADC∽△ACB，∴AD∶AC＝AC∶AB，∴AC²＝AB·AD.(2)∵E为AB的中点，∴CE＝BE＝AE，∴∠EAC＝∠ECA.∵∠DAC＝∠CAB，∴∠DAC＝∠ECA.又∵∠AFD＝∠CFE，∴△AFD∽△CFE.模型 3“母子”型相似三角形模型1．如图5，在Rt△ABC中，∠BAC＝90°，AD⊥BC，则有△ADB∽△CDA∽△CAB.2．如图6，在△ABC中，点D是BC边上一点，且∠ABC＝∠DAC，则有△DAC∽△ABC.5．在Rt△ABC中，∠ACB＝90°，D为AB边上一点，且CD⊥AB.(1)求证：AC2＝AB·AD；(2)若△ABC为任意三角形，试问：在AB边上(不包括A，B两个顶点)是否仍存在一点D，使AC2＝AB·AD，若存在，请加以证明；若不存在，请说明理由． (2)存在．理由如下： 6．如图，在△ABC中，BD⊥AC于点D，DE⊥AB于点E，BD·DE＝BE·CD.(1)求证：△BCD∽△BDE；(2)若BC＝10，AD＝6，求AE的长．    7．如图，在▱ABCD中，∠BAD的平分线交边BC于点E，交DC的延长线于点F，点G在AE上，连接GD，∠GDF＝∠F.(1)求证：AD2＝DG·AF；(2)连接BG，如果BG⊥AE，且AB＝6，AD＝9，求AF的长．   解：(1)∵点D是 的中点，∴∠ACD＝∠BAD.又∵∠ADE＝∠CDA，∴△ADE∽△CDA. 模型 4旋转型相似三角形模型等角的顶点重合且等角的两边对应成比例的两个三角形旋转——相似三角形，如图： 9．如图，已知四边形ABCD和EFCG均为正方形，点E在△ABC内，∠CAE＋∠CBE＝90°.(1)求证：△CAE∽△CBF；(2)若BE＝1，AE＝2，求BF和CE的长． 10．如图，在△ABC中，AB＝AC，△ADE∽△ABC，连接BD，CE.(1)判断BD与CE的数量关系，并证明你的结论；(2)若AB＝2√3，AD＝4，∠BAC＝120°，∠CAD＝30°.求BD的长．(1)BD＝CE.证明：∵△ADE∽△ABC，AB＝AC，∴∠BAC＝∠DAE，AD＝AE，∴∠BAC＋∠CAD＝∠CAD＋∠DAE，即∠BAD＝∠CAE.在△ABD与△ACE中，∴△ABD≌△ACE(SAS)，∴BD＝CE.   　45    模型 5“赵爽弦图”衍生的相似三角形模型一线三等角是有三个相等的角的顶点在同一条直线上构成的图形，这三个相等的角可以在同侧(在同侧时，三个等角可以是直角(如图①)，也可以是钝角(如图②)或锐角(如图③、图④)，也可以在异侧(如图⑤)．“一线三等角”模型也可称为“K字型”．注：这些模型常用来证明三角形的全等或相似． 解析：∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°，∴∠EBC＋∠BCE＝90°.∵∠BCE＋∠DCA＝90°，∴∠EBC＝∠DCA.在△CEB和△ADC中 ∴△CEB≌△ADC(AAS)，∴BE＝CD＝1，CE＝AD＝3.∴DE＝CE－CD＝2.B13．如图，AB，CD都是BD的垂线，AB＝4，CD＝6，BD＝14，P是BD上一点，连接AP，CP，所得两个三角形相似，则BP的长是 ．  14．如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为F，连接DF，求tan∠CAD的值．解：如图，设AD＝2a. 15．如图，在矩形ABCD中，已知AD＞AB.在边AD上取点E，连接CE.过点E作EF⊥CE，与边AB的延长线交于点F.(1)求证：△AEF∽△DCE；(2)若AB＝3，AE＝4，DE＝6，求线段BF的长．解：(1)证明：∵四边形ABCD是矩形，∴∠A＝∠D＝90°，∴∠AEF＋∠F＝90°.∵EF⊥CE，∴∠CED＋∠AEF＝180°－90°＝90°，∴∠CED＝∠F.又∵∠A＝∠D＝90°，∴△AEF∽△DCE. 16．如图，在等腰三角形ABC中，∠BAC＝120°，AB＝AC＝2，D是BC边上的一个动点(不与点B，C重合)，在AC上取一点E，使∠ADE＝30°.(1)求证：△ABD∽△DCE；(2)设BD＝x，AE＝y，求y关于x的函数关系式并写出自变量x的取值范围．解：(1)证明：∵△ABC是等腰三角形，∠BAC＝120°，∴∠B＝∠C＝30°，∴∠B＝∠ADE.∵∠ADC＝∠ADE＋∠EDC＝∠B＋∠DAB.∴∠DAB＝∠EDC.∴△ABD∽△DCE. 课程结束