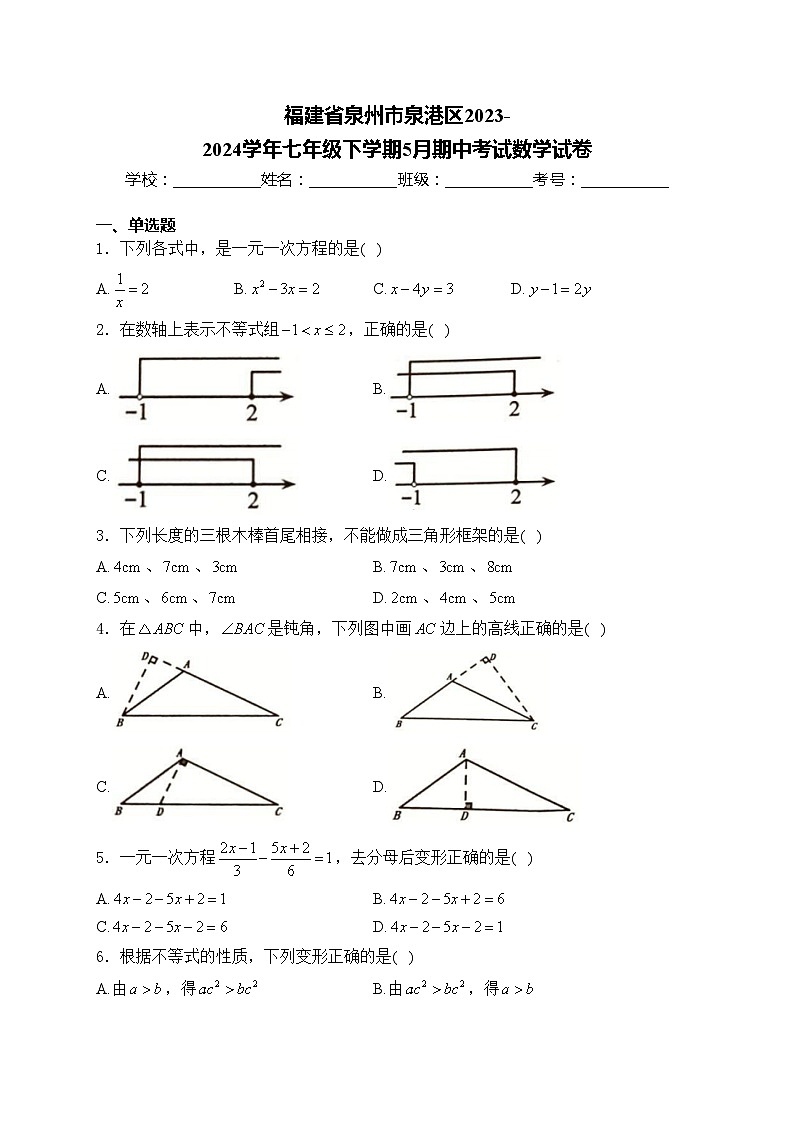
福建省泉州市泉港区2023-2024学年七年级下学期5月期中考试数学试卷(含答案)

这是一份福建省泉州市泉港区2023-2024学年七年级下学期5月期中考试数学试卷(含答案)，共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列各式中，是一元一次方程的是( )
A.B.C.D.
2．在数轴上表示不等式组，正确的是( )
A.B.
C.D.
3．下列长度的三根木棒首尾相接，不能做成三角形框架的是( )
A.、、B.、、
C.、、D.、、
4．在中，是钝角，下列图中画边上的高线正确的是( )
A.B.
C.D.
5．一元一次方程，去分母后变形正确的是( )
A.B.
C.D.
6．根据不等式的性质，下列变形正确的是( )
A.由，得B.由，得
C.由，得D.由，得
7．如图所示，一个正方形水池的四周恰好被4个正n边形地板砖铺满，则n等于( )
A.4B.6C.8D.10
8．用代入法解二元一次方程组过程中，下列变形不正确的是( )
A.由①得B.由①得
C.由②得D.由②得
9．我国古代数学著作《孙子算经》有“多人共车”问题：“今有三人共车，二车空；二人共车，九人步.问：人与车各几何？”其大意如下：有若干人要坐车，如果每3人坐一辆车，那么有2辆空车；如果每2人坐一辆车，那么有9人需要步行，问人与车各多少？设共有x人，y辆车，则可列方程组为( )
A.B.C.D.
10．张明同学的家庭作业中有这样一道题：，□处被墨水覆盖了，张明打电话问李晓同学，李晓告诉张明这个方程的解是，那么□处应该是数字( )
A.3B.4C.5D.
二、填空题
11．方程的解是______.
12．六边形的外角和等于______.
13．“y的2倍与8的和不小于”用不等式表示为______.
14．如图，是的中线，M是边上的中点，连接，若的面积为，则的面积为______.
15．关于x、y的二元一次方程组的解满足，则______.
16．非负数x，y满足，记，的最大值为m，最小值n，则______.
三、解答题
17．解方程：.
18．解方程组：.
19．解不等式组：，并把它们的解集在数轴上表示出来.
20．如图，在中，，，的外角的平分线交的延长线于点E.
（1）求的度数；
（2）过点D作，交的延长线于点F，求的度数.
21．某城市自来水收费实行阶梯水价，收费标准如下表所示：
（1）若小明家3月份用水量是15吨，则需交水费______元；
（2）若小明家3月份交水费60元，求小强家3月份用水量是多少吨？
22．阅读探索：解方程组.
解析：设，，原方程组可变为.
解方程组得：，即，解得.所以此种解方程组的方法叫换元法.
（1）运用上述方法解方程组：；
（2）已知关于x，y的方程组的解为，求出关于m，n的方程组的解.
23．对x，y定义一种新运算T，规定：（其中m，n均为非零常数）.
例如：.已知，.
（1）求m，n的值；
（2）若关于p的不等式组恰好有3个整数解，求a的取值范围.
24．基金会计划购买A、B两种纪念册共50册，已知B种纪念册的单价比A种的单价少10元，买3册A种纪念册与买4册B种纪念册的总费用为310元.
（1）求A、B两种纪念册的单价分别是多少元？
（2）如果购买的A种纪念册的数量要大于B种纪念册数量的，但又不大于B种纪念册数量的，设购买A种纪念册m册.
①有多少种不同的购买方案？
②购买时A种纪念册每册降价a元，B种纪念册每册降价b元.若满足条件的各购买方案所需的总费用相同，求总费用的最小值.
25．如图①，在中，与的平分线相交于点P.
（1）若，则的度数是______；
（2）如图②，作外角，的角平分线交于点Q，试探索，之间的数量关系.
（3）如图③，延长线段，交于点E，在中，存在一个内角等于另一个内角的3倍，求的度数.
参考答案
1．答案：D
解析：
2．答案：B
解析：
3．答案：A
解析：
4．答案：A
解析：
5．答案：C
解析：
6．答案：B
解析：
7．答案：C
解析：
8．答案：D
解析：
9．答案：C
解析：
10．答案：B
解析：
11．答案：
解析：
12．答案：
解析：
13．答案：
解析：
14．答案：3
解析：
15．答案：6
解析：
16．答案：21
解析：
17．答案：
解析：去括号得：，
移项得：，
合并得：，
系数化1得：.
18．答案：
解析：得：③，
得：，
解得：，
把代入①得：，
解得：，
原方程组的解是：.
19．答案：，数轴见解析
解析：解不等式①得：，
解不等式②得：，
在数轴上表示不等式①、②的解集如图：
原不等式组的解集为：.
20．答案：（1）
（2）
解析：（1）是的外角，
，
，，
，
平分，
；
（2），
，
由（1）得：，
，
，
.
21．答案：（1）31.5
（2）小明家3月份的用水量是25吨
解析：（1）31.5；
（2）如果一个月用水12吨，则需水费：（元），
如果一个月用水18吨，则需水费：（元），
，
3月份的用水量超过了18吨.
设小明家3月份用水量为x吨，
依题意可得：，
解得：，
答：小明家3月份的用水量是25吨.
22．答案：（1）
（2）
解析：（1）设，，
则原方程组可变形为：，
解得：，
，解得：；
（2）设，，
依题意得：，解得：.
23．答案：（1）
（2）
解析：（1）依题意得：
，解得：；
（2）由（1）可得：，
依题意得：，
解不等式①得：，
解不等式②得：，
不等式组恰好有3个整数解，
，
整数解有：0，1，2，
，
.
24．答案：（1）A种纪念册的单价为每本50元，B种纪念册的单价为每本40元
（2）①共有4种不同的购买方案
②总费用的最小值为1750元
解析：（1）设A种纪念册的单价为每本x元，B种纪念册的单价为每本y元，
依题意得：，解得：，
答：A种纪念册的单价为每本50元，B种纪念册的单价为每本40元.
（2）①依题意得：，
解得：，
m为正整数，
m可以取15，16，17，18，
共有4种不同的购买方案.
（2）设总费用为W元，则
，
满足条件的各购买方案所需的总费用相同，
，
，，
，
，
当时，W取最小值，最小值为，
即总费用的最小值为1750元.
25．答案：（1）
（2）
（3）的度数是或或或
解析：（1）；
（2），，
，
点Q是和的角平分线的交点
，，
，
；
（3）如图③，延长至点F，
为的外角的角平分线，
是的外角的角平分线，
，
平分，
，
，
，
即，
，
即，
平分，平分，，
，
如果在中，存在一个内角等于另一个内角的3倍，那么分为四种情况：
①当时，则，
；
②当时，则，，
；
③当时，则，
；
④当时，则，
.
综上所述，的度数是或或或.
月用水量
不超过12吨
的部分
超过12吨但
不超过18吨的部分
超过18吨
的部分
收费标准（元/吨）
2.00
2.50
3.00