2024年四川省成都市四川省成都市第七中学初中学校中考三模数学试题(无答案)

这是一份2024年四川省成都市四川省成都市第七中学初中学校中考三模数学试题(无答案)，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（满分150分，120分钟完成）
A卷（满分100分）
一、选择题（本大题共8个小题，每小题4分，共32分，每小题只有一项符合题目要求）
1.下列图案是中心对称图形但不是轴对称图形的是（ ）
A.B.C.D.
2.下列图形是棱锥侧面展开图的是（ ）
A.B.
C.D.
3.下列运算正确的是（ ）
A.B.
C.D.
4.在相同条件下的多次重复试验中，一个随机事件发生的频率为f，该事件的概率为P.下列说法正确的是（ ）
A.试验次数越多，f越大B.f与P都可能发生变化
C.试验次数越多，f越接近于PD.当试验次数很大时，f在P附近摆动，并趋于稳定
5.已知一组数据：23，22，24，23，23，这组数据的方差是（ ）
A.3B.2C.D.
6.元朝朱世杰所著的《算学启蒙》中，记载了这样一道题：良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之?其大意是：快马每天行240里，慢马每天行150里，慢马先行12天，快马几天可追上慢马?若设快马x天可追上慢马，由题意得（ ）
A.B.
C.D.
7.如图所示，把两张矩形纸条交叉叠放在一起，重合部分构成一个四边形ABCD.固定一张纸条，另一张纸条在转动过程中，下列结论一定成立的是（ ）
A.四边形ABCD的周长不变B.四边形ABCD的面积不变
C.D.
8.已知二次函数（为常数，且），下列结论：①函数图象一定经过第一、二、四象限；②函数图象一定不经过第三象限；③当时，y随x的增大而减小；④当时，y随x的增大而增大.其中所有正确结论的序号是（ ）
A.①②B.②③C.②D.③④
二、填空题（本大题共5个小题，每小题4分，共20分）
9.9的算术平方根是_________.
10.如图，AB是的直径，CD是的弦，，则的度数是_________.
11.已知点，在抛物线上，且，则__________.（填“”或“=”）
12.关于x的方程有两个相等的实数根，则k的值为___________.
13.如图，中，，，，以点B为圆心，适当长为半径画弧，分别交BA、BC于点M、M，再分别以点M、N为圆心，大于的长为半径画弧，两弧交于点E，作射线BE交AC于点D，则线段AD的长为_________.
三、解答题（本大题共5个小题，共48分）
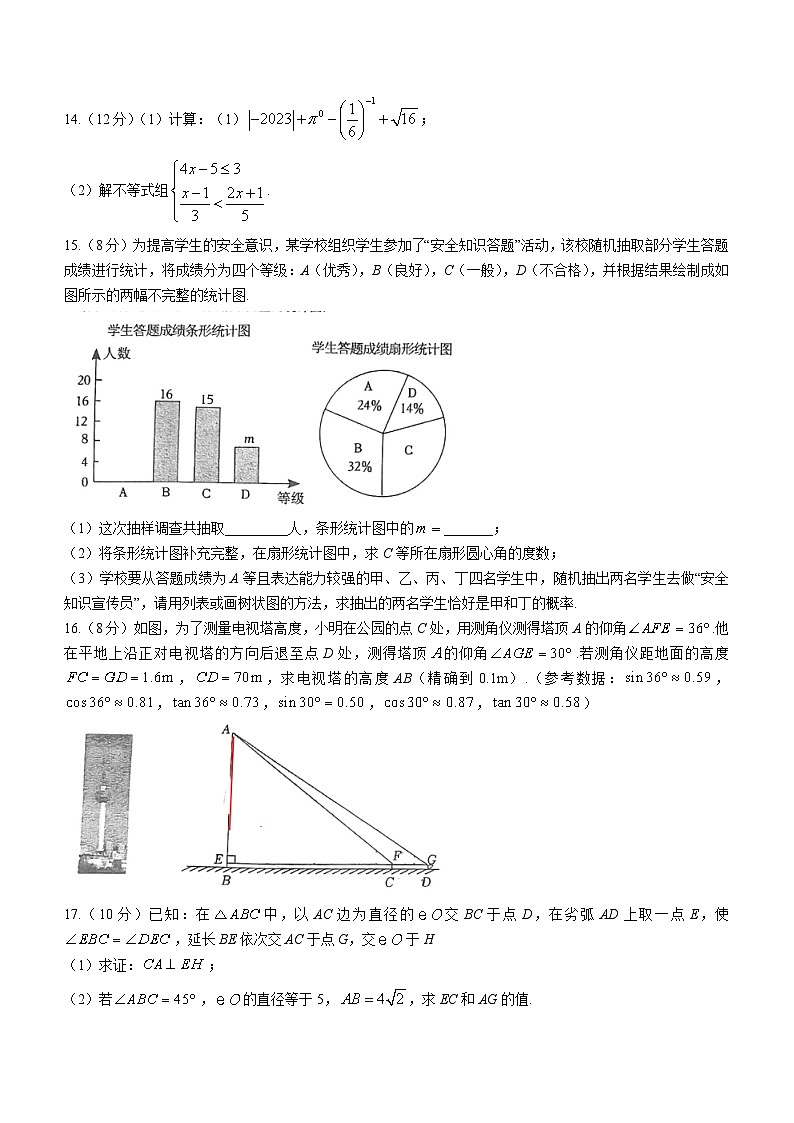
14.（12分）（1）计算：（1）；
（2）解不等式组.
15.（8分）为提高学生的安全意识，某学校组织学生参加了“安全知识答题”活动，该校随机抽取部分学生答题成绩进行统计，将成绩分为四个等级：A（优秀），B（良好），C（一般），D（不合格），并根据结果绘制成如图所示的两幅不完整的统计图.
（1）这次抽样调查共抽取_________人，条形统计图中的_______；
（2）将条形统计图补充完整，在扇形统计图中，求C等所在扇形圆心角的度数；
（3）学校要从答题成绩为A等且表达能力较强的甲、乙、丙、丁四名学生中，随机抽出两名学生去做“安全知识宣传员”，请用列表或画树状图的方法，求抽出的两名学生恰好是甲和丁的概率.
16.（8分）如图，为了测量电视塔高度，小明在公园的点C处，用测角仪测得塔顶A的仰角.他在平地上沿正对电视塔的方向后退至点D处，测得塔顶的仰角.若测角仪距地面的高度，，求电视塔的高度AB（精确到0.1m）.（参考数据：，，，，，）
17.（10分）已知：在中，以AC边为直径的交BC于点D，在劣弧AD上取一点E，使，延长BE依次交AC于点G，交于H
（1）求证：；
（2）若，的直径等于5，，求EC和AG的值.
18.（10分）如图，在平面直角坐标系中，一次函数与反比例函数交于点和点B.
（1）求k和a的值，及点B坐标；
（2）将直线AB沿着y轴向上平移m个单位与x轴，y轴分别交于点C，点D，若，求m的值；
（3）若点在反比例函数图象上，点F是线段AE延长线上一点，过点F作直线，交反比例函数于点，若，求点G的坐标.
B卷（共50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19.已知，，则__________.
20.关于x的分式方程的解为正数，则m的取值范围是___________.
21.《九章算术》中记载：“今有勾八步，股一十五步.问勾中容圆径几何?”译文：今有一个直角三角形，勾（短直角边）长为8步，股（长直角边）长为15步，问该直角三角形内切圆的直径是多少?书中给出的算法译文如下：如图，根据勾、股，求得弦长.用勾、股、弦相加作为除数，用勾乘以股，再乘以2作为被除数，商即为该直角三角形内切圆的直径，求得该直径等于_________步（注：“步”为长度单位）.
22.如图，在中，，D为AC边上的中点，将沿BD翻折至，连接CE，若，则___________.
23.平面直角坐标系中，的半径为1，A、B为外两点，.
给出如下定义：平移线段AB，得到的弦（，分别为点A，B的对应点），线段长度的最小值称为线段AB到的“平移距离”.若点A的坐标为（4，3），记线段AB到的“平移距离”为d，d的取值范围为_____________.
二、解答题（本大题共3个小题，共30分）
24.（8分）近年来，市民交通安全意识逐步增强，头盔需求量增大，某商店购进甲、乙两种头盔，已知购买甲种头盔20只，乙种头盔30只，共花费2920元，甲种头盔的单价比乙种头盔的单价高11元.
（1）甲、乙两种头盔的单价各是多少元?
（2）商店决定再次购进甲、乙两种头盔共40只，正好赶上厂家进行促销活动，促销方式如下：甲种头盔按单价的八折出售，乙种头盔每只降价6元出售.如果此次购买甲种头盔的数量不低于乙种头盔数量的一半，那么应购买多少只甲种头盔，使此次购买头盔的总费用最小?最小费用是多少元?
25.（10分）抛物线：与x轴交于点，，与y轴交于点C.
（1）求抛物线的表达式；
（2）如图1，点D是抛物线上的一个动点，设点D的横坐标是，过点D作直线轴，垂足为点E，交直线AC于点F.当D，E，F三点中一个点平分另外两点组成的线段时，求线段DF的长；
（3）如图2，将抛物线水平向左平移，使抛物线恰好经过原点，得到抛物线，直线：交抛物线于P、Q，若，求原点O到PQ距离的最大值.
26.（12分）如图，矩形ABCD中，，，点E，F分别为边AB，BC上的点，将线段EF绕点F顺时针旋转60°，得到线段FG.射线FG与对角线AC交于点M，连接EM，EG.
（1）求的度数：
（2）若，求的值；
（3）连接CG，DG，若，设和的面积分别为，，当点E在边AB上运动时，求的最大值及此时AE的长.