2024年湖南省长沙市初中学业水平考试数学押题卷（五）

这是一份2024年湖南省长沙市初中学业水平考试数学押题卷（五），共9页。试卷主要包含了00003kg左右，0等内容，欢迎下载使用。
温馨提示：
1.答题前，请考生先将自己的姓名、准考证号填写清楚，并认真核对条形码上的姓名、准考证号、考室和座位号；
2.必须在答题卡上答题，在草稿纸、试题卷上答题无效；
3.答题时，请考生注意各大题题号后面的答题提示；
4.请勿折叠答题卡，保持字体工整、笔迹清晰、卡面清洁；
5.答题卡上不得使用涂改液、涂改胶和贴纸；
6.本学科试卷共25个小题，考试时量120分钟，满分120分．
一、选择题（在下列各题的四个选项中，只有一项是符合题意的. 请在答题卡中填涂符合题意的选项. 本大题共10个小题，每小题3分，共30分）
1．在实数1，−1，0，−2中，绝对值最大的数是（ ）
A．1B．−1C．0D．−2
2．下列航天图标中，其文字上方的图案是中心对称图形的是（ ）
A．B．C．D．
3．2024年初春，全国范围内迎来了大降雪，“忽如一夜春风来，千树万树梨花开”，这是唐代诗人岑参描写雪花最新奇的诗句．据悉单片雪花很轻，只有0.00003kg左右，0.00003用科学记数法可以表示为（ ）
A．3×10−5B．3×10−4C．0.3×10−4D．0.3×10−5
4．在“甲骨文文化”知识竞赛中，某学习小组的得分（单位：分）依次为80，76，74，73，72，76，那么这组数据的众数是（ ）
A．74B．75C．76D．80
5．如图，三根木棒a，b，c钉在一起，∠1=65°，现要使a∥b，则∠2的大小为（ ）
第5题图 第6题图 第8题图
A．130°B．125°C．115°D．95°
6．如图，等腰△ABC中，AB=AC，D为BC的中点，则下列结论不正确的是（ ）
A．∠B=∠C B．AD⊥BC C．∠BAD=∠CAD D．AB=2BC
7．下列一次函数中，y随x的增大而减小的函数是（ ）
A．y=5x+3B．y=x−2C．y=xD．y=−8x−5
8．如图，A，B两地被池塘隔开，小明先在AB外选一点C，然后测出AC,BC的中点M，N，若MN的长为16米，则A，B间的距离是（ ）
A．18米B．20米C．24米D．32米该试卷源自 全站资源不到一元，每日更新。 9．如图，圆弧形桥拱的跨度AB为24米，拱桥所在圆的半径为13米，则拱高CD为（ ）
A．2米B．4米C．8米D．10米
第9题图 第10题图
10．中国奇书《易经》中记载，远古时期，人们通过在绳子上打结来计数，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满5进1，用来记录孩子自出生后的天数．由图可知，孩子自出生后的天数是（ ）
A．10B．89C．165D．294
二、填空题（本大题共8小题，每小题3分，共24分）
11．因式分解：a2−4= ．
12．方程1x=23x−1的解为 ．
第13题图 第15题图 第16题图
13．如图，在⊙O中，点C为优弧ACB上的一点，AB=168°，则∠C= ．
14．如图，有四张形状、大小、质地均相同的卡片，正面分别印有“速度滑冰”、“冰球”、“单板滑雪”、 ‘冰壶“四种不同的图案，现将这四张卡片背面朝上洗匀，从中随机抽取一张卡片，则该卡片的正面图案恰好是“冰壶”的概率是
15．如图，点A在反比例函数y=12x的图像上，过点A作AB⊥y轴于点B，C为x轴上的一点，连接AC，BC，则△ABC的面积为 ．
16．如图，在▱ABCD中，以点A为圆心AB长为半径作弧交AD于点F，分别以点B、F为圆心，同样长度m为半径作弧，交于点G，连接AG并延长交BC于点E，若BF=6，AB=4，则AE的长为 ．
三、解答题（本大题共8小题，第19、20题每小题6分，第21、22题每小题8分，第23、24题每小题9分，第25、26题每小题10分）
17．计算：(π−1)0+3−2+12−(12)−1．
18．先化简，再求值：x+2x−2+31−x,其中x=2．
19．如图，育才学校教学楼AB的后面有一建筑物CD，当光线与地面的夹角是25°时，教学楼在建筑物的墙上留下高3m的影子CE，而当光线与地面夹角是45°时，教学楼顶点A在地面上的影子点F与墙角点C有20m的距离（B，F，C在同一条直线上，结果精确到1m，参考数据：sin25°=0.42，cs25°=0.91，tan25°=0.47）
（1）求教学楼AB的高度；
（2）请你求出点A，E之间的距离．
20．抗美援朝战争是新中国的立国之战，中国人民志愿军打破了美军不可战胜的神话．电影《长津湖》将这一段波澜壮阔的历史重新带进了人们的视野，并一举拿下了国庆档的票房冠军，激发了大家的爱国热情．因此，某校开展了抗美援朝专题知识竞赛，所有同学得分都不低于80分，现从该校八、九年级中各抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用x（分）表示，共分成四个等级，A：80≤x＜85；B：85≤x＜90；C：90≤x＜95；D：95≤x＜100），下面给出了部分信息：
八年级抽取的学生C等级的成绩为：92，92，93，94
九年级抽取的学生D等级的成绩为：95，95，95，97，100
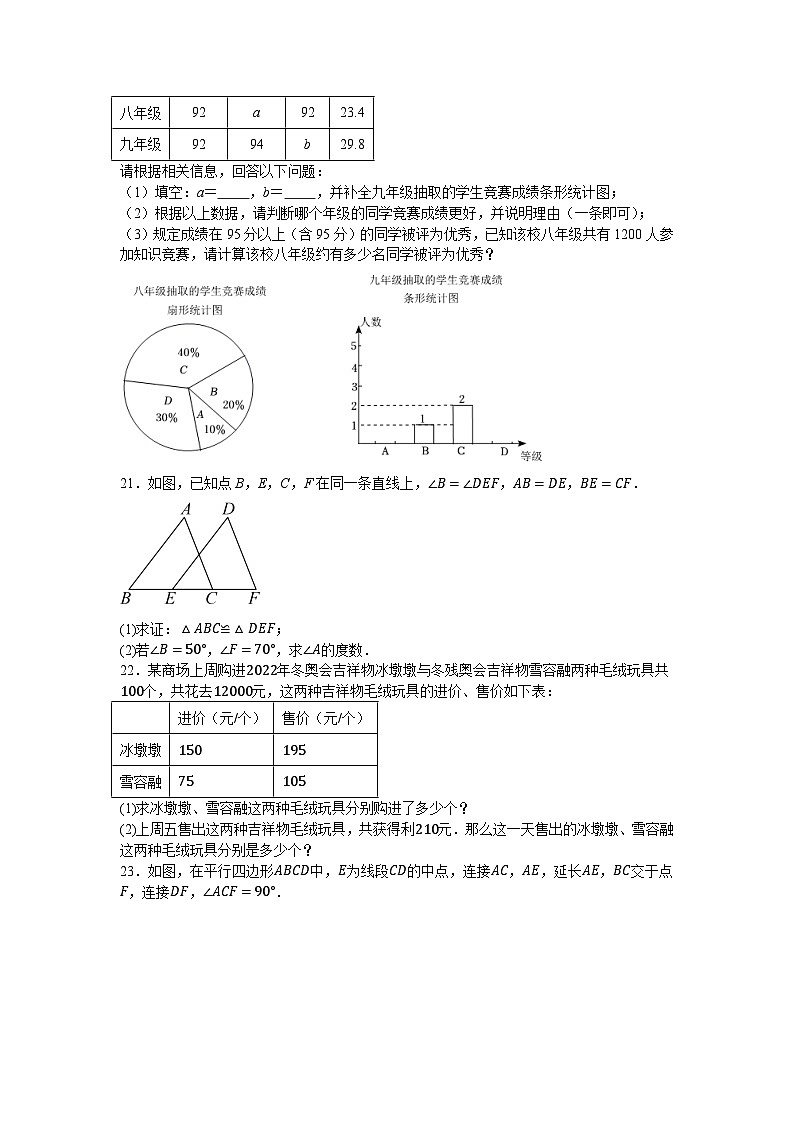
八，九年级抽取的学生竞赛成绩统计表：
请根据相关信息，回答以下问题：
（1）填空：a＝ ，b＝ ，并补全九年级抽取的学生竞赛成绩条形统计图；
（2）根据以上数据，请判断哪个年级的同学竞赛成绩更好，并说明理由（一条即可）；
（3）规定成绩在95分以上（含95分）的同学被评为优秀，已知该校八年级共有1200人参加知识竞赛，请计算该校八年级约有多少名同学被评为优秀？
21．如图，已知点B，E，C，F在同一条直线上，∠B=∠DEF，AB=DE，BE=CF．

(1)求证：△ABC≌△DEF；
(2)若∠B=50°，∠F=70°，求∠A的度数．
22．某商场上周购进2022年冬奥会吉祥物冰墩墩与冬残奥会吉祥物雪容融两种毛绒玩具共100个，共花去12000元，这两种吉祥物毛绒玩具的进价、售价如下表：
(1)求冰墩墩、雪容融这两种毛绒玩具分别购进了多少个？
(2)上周五售出这两种吉祥物毛绒玩具，共获得利210元．那么这一天售出的冰墩墩、雪容融这两种毛绒玩具分别是多少个？
23．如图，在平行四边形ABCD中，E为线段CD的中点，连接AC，AE，延长AE，BC交于点F，连接DF，∠ACF=90°．

(1)求证：四边形ACFD是矩形；
(2)若CD=13，CF=5，求四边形ABCE的面积．
24．如图，⊙O为等边ΔABC的外接圆，半径为2，点D在劣弧AB上运动（不与点A,B重合），连接DA，DB，DC．
（1）求证：DC是∠ADB的平分线；
（2）四边形ADBC的面积S是线段DC的长x的函数吗？如果是，求出函数解析式；如果不是，请说明理由；
（3）若点M,N分别在线段CA，CB上运动（不含端点），经过探究发现，点D运动到每一个确定的位置，ΔDMN的周长有最小值t，随着点D的运动，t的值会发生变化，求所有t值中的最大值．
25．定义：平面直角坐标系xOy中，若点Pm，n，点Qkm，−kn，且k≠0，则称点Q是点P的“k级变换点”．例如，点−4，8是2，4的“−2级变换点”．
(1)函数y=−6x的图象上是否存在点3，1的“k级变换点”？若存在，求出k的值，若不存在，说明理由；
(2)点A为直线l1：y=12x−3上的一点，它的“k级变换点”B在直线l2上，直接写出直线l2的函数表达式．
(3)若关于x的二次函数y=ax2+2b−12x+3c−5a≠0的图象上恰有两个点Ax1，y1，Bx2，y2，这两个点的“1级变换点”都在直线y=x+5上，并且同时满足：①a+b+c=0，②a>b>c，求x1−x2的取值范围．
参考答案与解析
一、选择题
二、填空题
11．a+2a−2 12．x=1 13．84°
14．14 15．6 16．27
三、解答题
17．【详解】解：原式=1+2−3+23−2
=1+3．
18．【详解】解：原式=x2−4+3−3x
=x2−3x−1当x=2时，原式=(2)2−32−1
=2−32−1，
=1−32．
19．【详解】解：（1）如图所示，过点E作EM⊥AB于点M，
∴四边形MBCE为矩形，
∴MB=CE=3，ME=BC，
设AB=xm，
在RtΔABF中，∵∠AFB=45°，
∴BF=AB=x，
∴ME=BC=BF+FC=x+20，
在RtΔAME中，
∵∠AEM=25°，AM=AB−MB=x−3，
∴tan25°=AMME=x−3x+20，
∴x−3x+20≈0.47，
解得x≈23，
答：办公楼AB的高度约为23m．
（2）在RtΔAME中，∵cs25°=MEAE，
∴AE=MEcs25°=23+200.91≈47m，
答：A，E之间的距离约为47m．
20．【详解】解：（1）由题意可知，八年级10名同学成绩从小到大排列后，处在中间位置的两个数是92，93因此中位数是92.5，即a＝92.5；
九年级10名学生成绩出现次数最多的是95，共出现3次，因此众数是95，即b＝95，
九年级10名学生成绩处在“A组”的有10﹣1﹣2﹣5＝2（人），补全频数分布直方图如下：
故答案为：92.5；95；
（2）九年级成绩较好，理由：九年级学生成绩的中位数、众数都比八年级的高；
（3）1200×30%＝360（名），
故该校八年级约有360名同学被评为优秀．
21．【详解】（1）证明：∵BE=CF，
∴BE+EC=CF+EC，即BC=EF，
在△ABC和△DEF中，AB=DE∠B=∠DEFBC=EF，
∴△ABC≌△DEFSAS；
（2）解：由△ABC≌△DEF得∠ACB=∠F．
∵∠B=50°，∠F=70°，
∴∠A=180°−∠ACB−∠B=180°−∠F−∠B=60°，
22．【详解】（1）解：设购进冰墩墩毛绒玩具x个，雪容融毛绒玩具y个，
依题意得：x+y=100150x+75y=12000，解得：x=60y=40．
∴购进冰墩墩毛绒玩具60个，雪容融毛绒玩具40个．
（2）解：设售出冰墩墩毛绒玩具m个，雪容融毛绒玩具n个，
依题意得：(195−150)m+(105−75)n=210，
∴n=7−32m．
又∵m，n均为正整数，∴m=2n=4或m=4n=1．
∴售出冰墩墩毛绒玩具2个，雪容融毛绒玩具4个或售出冰墩墩毛绒玩具4个，雪容融毛绒玩具1个．
23．【详解】（1）∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DAF=∠AFC，∠ADC=∠DCF，
∵E为线段CD的中点，
∴DE=CE，
∴△ADE≅△FCE，
∴AE=EF，
∴四边形ACFD是平行四边形，
∵∠ACF=90°，
∴平行四边形ACFD是矩形．
（2）过点E作EG⊥AC于点G，
∵四边形ABCD是平行四边形，
∴AD=BC，
∵四边形ACFD是矩形，
∴AD=CF，
∴AD=BC=CF=5，
∵CD=13，
∴DF=132−52=12，
∴四边形ABCE的面积等于S△ABC+S△AEC，
∵S△ABC=12×AC×BC=12×12×5=30，S△ACE=12×AC×GE，
∵点E是对角线的中心，
∴GE=12AD=52，
∴S△ACE=12×AC×GE=12×12×52=15，
∴平行四边形ABCE的面积为：30+15=45．
24．【详解】(1)∵△ABC为等边三角形,BC=AC，
∴ AC⏜=BC⏜,都为13圆，
∴∠AOC=∠BOC=120°，
∴∠ADC=∠BDC=60°，
∴DC是∠ADB的角平分线．
(2)是．如图，延长DA至点E，使得AE=DB．
连接EC，则∠EAC=180°－∠DAC＝∠DBC．
∵AE＝DB，∠EAC＝∠DBC,AC＝BC，
∴△EAC≌△DBC(SAS)，
∴∠E=∠CDB=∠ADC=60°，
故△EDC是等边三角形，
∵DC=x，∴根据等边三角形的特殊性可知DC边上的高为32x
∴S=S△DBC+S△ADC=S△EAC+S△ADC=S△CDE=12⋅x⋅32x=34x2(23b>c，a+b+c=0，可知a>0，c0，
∵x1+x2=−2ba，x1x2=3ca，
∴x1−x22=(x1−x2)2−4x1x2=−2ba2−4×3ca=4b2−12aca2，
由a>b>c，a+b+c=0，可知b=−(a+c)，
∴a>−(a+c)>c，
∴a>−(a+c)−(a+c)>c，
解得−2