北京市西城区华夏女子中学2023-2024学年八年级下学期期中数学试题(无答案)

这是一份北京市西城区华夏女子中学2023-2024学年八年级下学期期中数学试题(无答案)，共7页。试卷主要包含了考试结束，请将考试材料一并交回，若定义一种新运算等内容，欢迎下载使用。

初二数学试题
班级______ 姓名______ 学号______
注意事项：
1.本试卷共8页，满分100+10分，考试时间100分钟。
2.在试卷和答题卡上准确填写班级、姓名和学号
3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。
4.在答题卡上，选择题、画图题用2B铅笔作答，其他试题用黑色字迹签字笔作
答。
5.考试结束，请将考试材料一并交回。
一、单项选择题：本大题共8小题。每题3分，共24分。在每小题给出的四个选项中，只有一项符合题目的要求。把正确答案填涂在答题卡上。
1.下列二次根式中，最简二次根式是（ ）
A.B.C.D.
2.下列各式中，从左向右变形正确的是（ ）
A.B.C.D.
3.以下列长度的三条线段为边，能组成直角三角形的是（ ）
A.，，B.，，C.，，D.，，
4.如图，在中，，，则的度数是（ ）
A.B.C.D.
5.如图，在平面直角坐标系中，矩形的顶点，的坐标分别是，，点在轴上，则点的横坐标是（ ）
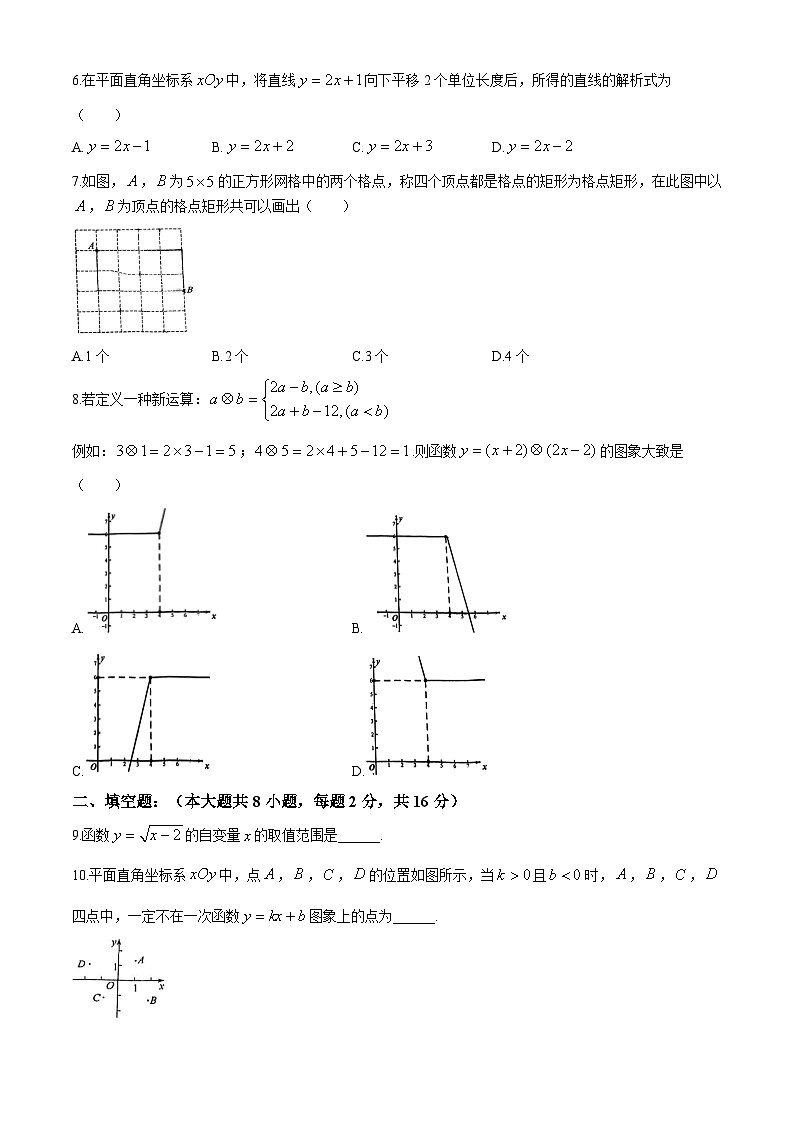
A.4B.C.5D.该试卷源自 全站资源不到一元，每日更新。 6.在平面直角坐标系中，将直线向下平移2个单位长度后，所得的直线的解析式为（ ）
A.B.C.D.
7.如图，，为的正方形网格中的两个格点，称四个顶点都是格点的矩形为格点矩形，在此图中以，为顶点的格点矩形共可以画出（ ）
A.1个B.2个C.3个D.4个
8.若定义一种新运算：
例如：；.则函数的图象大致是（ ）
A.B.
C.D.
二、填空题：（本大题共8小题，每题2分，共16分）
9.函数的自变量的取值范围是______.
10.平面直角坐标系中，点，，，的位置如图所示，当且时，，，，四点中，一定不在一次函数图象上的点为______.
11.如图，在中，点，点分别是，的中点，点是上一点，且，若，，则的长为______.
12.如图，菱形的对角线，相交于点，为边上一动点（不与点，重合），于点，于点，若，，则的最小值为______.
13.若直线与两条坐标轴围成的三角形的面积是2，则的值为______.
14.我国三国时期数学家赵爽为了证明勾股定理，绘制了一幅“弦图”，后人称其为“赵爽弦图”如图1所示.在图2中，若正方形的边长为7，正方形的边长为1，且，则正方形的边长为______.
图1图2
15.如图，把矩形沿直线向上折叠，使点落在点的位置上，交于点，若，，则的长为______.
16.在中，为的中点，点，为同一边上任意两个不重合的动点（不与端点重合），，的延长线分别与的另一边交于点，.下面四个推断：
①
②
③若是菱形，则至少存在一个四边形是菱形
④对于任意的，存在无数个四边形是矩形
其中，所有正确的有______.
三、解答题：（本大题共10小题，17题10分，18、19每题5分，20-23题每题6分，24、25题每题8分，共60分）
17.（1）
（2）已知，求代数式的值.
18.已知：为锐角三角形，.
求作：菱形.
作法：如图
①以点为圆心，适当长为半径作弧，交于点，交于点；
②分别以点，为圆心，大于的长为半径作弧，
两弧在的内部相交于点，作射线与交于点；
③以点为圆心，以长为半径作弧，与射线交于点，点和点分别位于的两侧，连接，；
四边形就是所求作的菱形.
（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
（2）完成下面的证明.
证明：由作法可知，平分，
，
______.
，
四边形是平行四边形.（______）.（填推理的依据）.
四边形是菱形（______）（填推理的依据）。
19.在本学期小组活动中，在平行四边形中添加线段，得到相应的基本图形，其中有一个小组画出的图形如图：
中，点，分别在边，上，且，连结，.求证：.
20.平面直角坐标系中，直线与直线交于点.
（1）求，的值；
（2）直线与直线，分别交于，两点，当时，若以，，，为顶点的四边形是平行四边形，请直接写出点的坐标.
21.如图，在中，平分交于点，过点作于点，交于点，连接.
（1）求证：四边形是菱形；
（2）连接，若，，，求菱形的面积.
22.有这样一个问题：探究函数的图象，并利用函数解决问题.小爱同学根据学习函数的经验，对函数的图象进行了探究.下面是小爱同学的探究过程，请补充完整：
（1）函数的自变量的取值范围是______.
（2）下表是与的几组对应值.
其中的值为______.
（3）如下图，在平面直角坐标系中，描出了以上表中各组对应值为坐标的点.根据描出的点，画出该函数的图象；
（4）结合图象解决问题：当时，的值约为______.
23.下表是一次函数（，为常数，）中与的两组对应值.
（1）求这个一次函数的表达式；
（2）已知直线，当时，对于的每一个值，都有，直接写出的取值范围.
24.在数学课上，老师说统计学中常用的平均数不是只有算术平均数一种，好学的小聪通过网络搜索，又得到了两种平均数的定义，他把三种平均数的定义整理如下：
对于两个数，，
称为，这两个数的算术平均数，
称为，这两个数的几何平均数，
称为，这两个数的平方平均数.
小聪根据上述定义，探究了一些问题，下面是他的探究过程，请你补充完整：
（1）若，，则______，______，______；
（2）小聪发现当，两数异号时，在实数范围内没有意义，所以决定只研究当，都是正数时这三种平均数的大小关系.结合乘法公式和勾股定理的学习经验，他选择构造几何图形，用面积法解决问题：
如图，画出边长为的正方形和它的两条对角线，则图1中阴影部分的面积可以表示.
图1图2图3
①请分别在图2，图3中用阴影标出一个面积为，的图形；
②借助图形可知当，都是正数时，，，的大小关系是：______（把，，从小到大排列，并用“”或“”号连接）.
③当时，的最大值是______.
25.点在正方形的边上（不与点，重合），点关于直线的对称点为，作射线交交于点，连接.
（1）求证：；
（2）过点作交射线于点.
①求的度数；
②用等式表示线段与之间的数量关系，并证明.…
1
2
…
…
3
5
3
…
0