初中数学人教版八年级上册第十二章 全等三角形12.3 角的平分线的性质课文ppt课件

这是一份初中数学人教版八年级上册第十二章 全等三角形12.3 角的平分线的性质课文ppt课件，共22页。PPT课件主要包含了学习目标，几何语言，角平分线的性质，复习回顾，新课导入，自学指导，推进新课，知识点一，角平分线的判定，作射线OP等内容，欢迎下载使用。
掌握角平分线判定定理的证明方法并解决相关问题
会判断一个点是否在一个角的平分线上
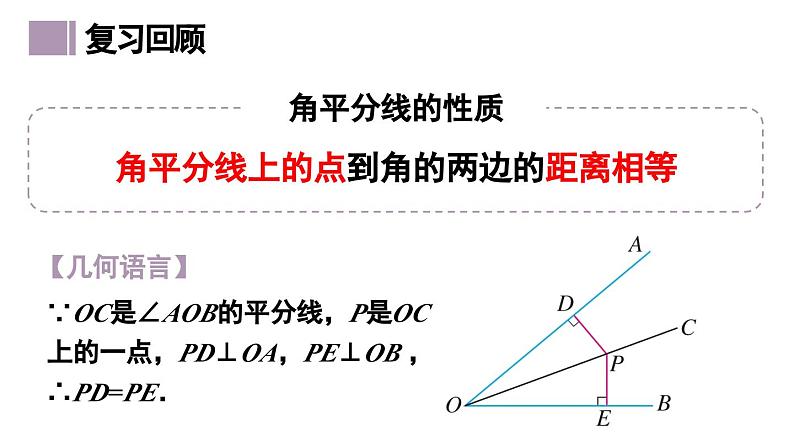
∵OC是∠AOB的平分线，P是OC上的一点，PD⊥OA，PE⊥OB ，∴PD=PE．
角平分线上的点到角的两边的距离相等
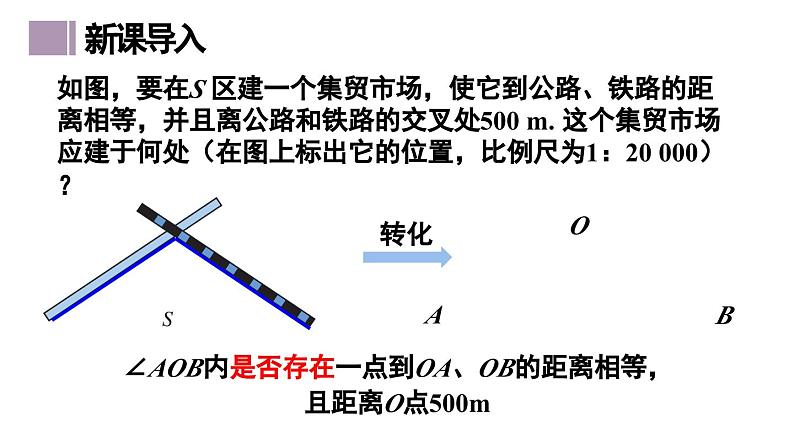
如图，要在S 区建一个集贸市场，使它到公路、铁路的距离相等，并且离公路和铁路的交叉处500 m. 这个集贸市场应建于何处（在图上标出它的位置，比例尺为1：20 000）？
∠AOB内是否存在一点到OA、OB的距离相等，且距离O点500m
认真看课本49-50页内容，5分钟内完成：1.课本49页思考题.2.角平分线判定的内容是什么？3.尝试总结角平分线判定定理的几何语言.
动脑思考.动手标记课本中的重点和疑点.5分钟后检测学习成果！
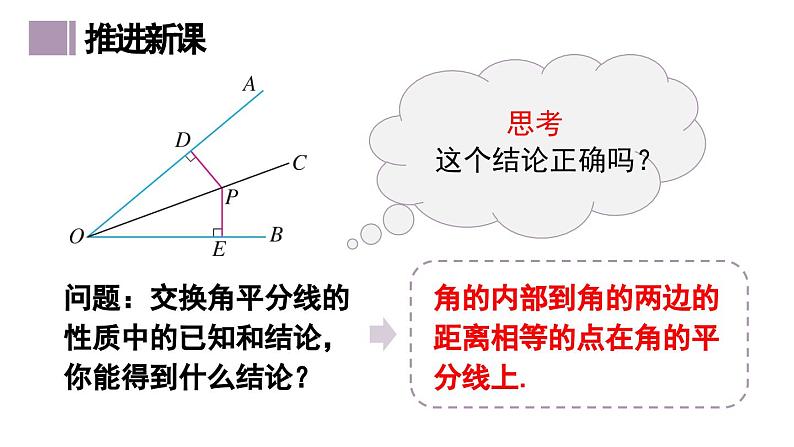
问题：交换角平分线的性质中的已知和结论，你能得到什么结论？
角的内部到角的两边的距离相等的点在角的平分线上.
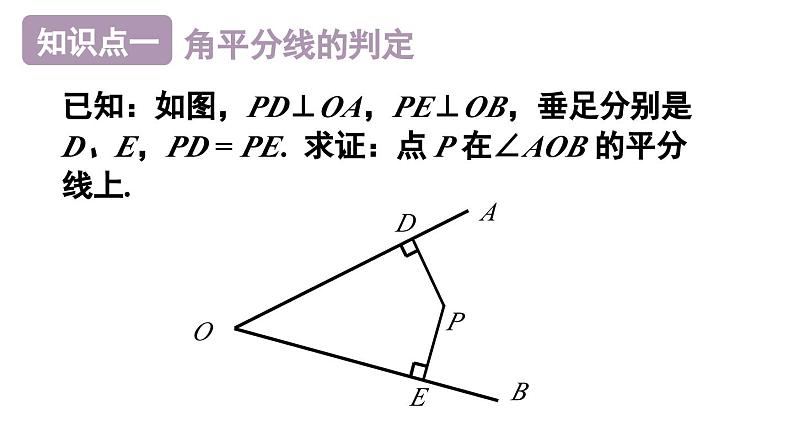
已知：如图，PD⊥OA，PE⊥OB，垂足分别是 D、E，PD = PE. 求证：点 P 在∠AOB 的平分线上.
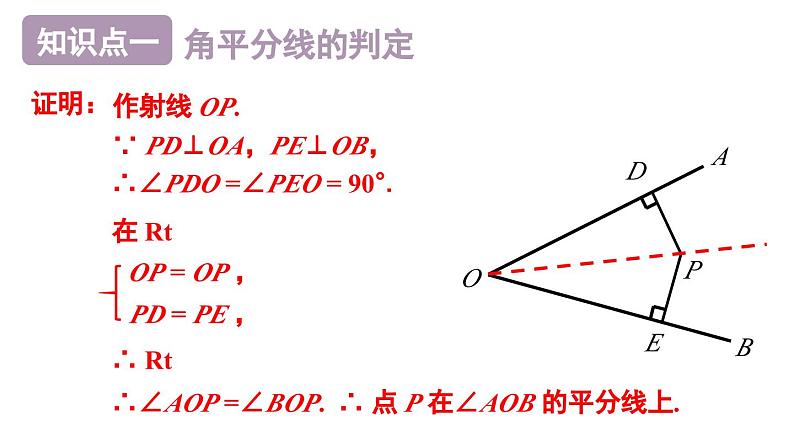
∴ 点 P 在∠AOB 的平分线上.
在 Rt△PDO 和 Rt△PEO 中，
∵ PD⊥OA，PE⊥OB，
∴∠PDO =∠PEO = 90°.
∴ Rt△PDO≌Rt△PEO （HL）.
∴∠AOP =∠BOP.
角的内部到角的两边的距离相等的点在角的平分线上
∵PD⊥OA，PE⊥OB，PD = PE∴点 P 在∠AOB的平分线上（OP 平分 ∠AOB）．
作夹角的角平分线 OC ， 截取 OD =2.5cm，D 即为所求.
∴图上距离 = 0.025m = 2.5cm.
如图，△ABC 的角平分线 BM，CN 相交于点 P．求证：点 P 到三边 AB，BC，CA 的距离相等．
证明：过P 点作 PD，PE，PF分别垂直于 AB，BC，CA，垂足分别为 D，E，F.∵BM 是△ABC的角平分线，点P 在BM 上，∴PD = PE .同理 PE = PF .∴ PD = PE = PF .即点P 到三边AB，BC，CA 的距离相等．
【结论】三角形的三条内角平分线交于一点，并且这点到三边的距离相等.
到三角形三边所在直线距离相等的点有几个呢？
OP平分∠AOBPD⊥OA于点DPE⊥OB于点E
PD⊥OA于点DPE⊥OB于点EPD=PE
1. 如图，O 是△ABC 内一点，且点 O 到三边 AB，AC，BC 的距离相等，即 OF = OE = OD，若∠BAC = 100°，则∠BOC 的度数是（ ）
A. 140° B. 130°C. 120° D. 110°
2.如图，△ABC的三边AB、AC、BC的长分别是5、7、9，其三条角平分线将△ABC分成三个三角形，则S△OAB: S△OAC: S△OBC =________.
3 如图，△ABC 的∠ABC 的外角的平分线 BD 与∠ACB 的外角的平分线 CE 相交于点 P . 求证：点 P 到三边 AB，BC，CA 所在直线的距离相等.
【课本P50 练习 第2题】
∴PM = PN，同理PN = PQ，∴点P到三边AB，BC，CA的距离相等.
证明：过P作PM⊥AC于M，PN⊥BC 于N，PQ⊥AB于Q. ∵CE为∠MCN的平分线，
4.如图，在△ABC中，∠B=∠C，DE⊥AB，DF⊥AC，垂足分别是E、F，BE=CF. 求证：AD平分∠BAC.
证明：∵DE⊥AB，DF⊥AC∴∠BED=∠CFD=90°在△BED和△CFD中，
∴△BED≌△CFD（ASA）.∴DE=DF，∴AD是∠BAC的平分线，即AD平分∠BAC
5. 如图，四边形ABCD中，∠B=∠C=90°，E为BC的中点，且AE平分∠BAD.求证：①DE平分∠ADC
证明：①如图，过点E作EF⊥AD于F， ∵∠B=90°，∴AE平分∠DAB， ∴EB=EF. ∵E是BC的中点，∴BE=CE ∴EF=CE. 又∠C=90°，EF⊥AD， ∴DE平分∠ADC.
5. 如图，四边形ABCD中，∠B=∠C=90°，E为BC的中点，且AE平分∠BAD.求证：②AB+CD=AD.
②在Rt△AEB和Rt△AEF中，
∴Rt△AEB≌Rt△AEF（HL），∴AB=AF.同理DC=DF，∴AB+CD=AF+FD=AD，∴AB+CD=AD.