初中数学人教版八年级上册13.3.1 等腰三角形备课ppt课件

这是一份初中数学人教版八年级上册13.3.1 等腰三角形备课ppt课件，共18页。PPT课件主要包含了ABAC，△ABC是等腰三角形等内容，欢迎下载使用。

经历探究等腰三角形的性质的过程，能用全等的知识验证性质，培养观察、分析、归纳和合情推理的能力掌握等腰三角形的性质会用等腰三角形的性质解决有关问题
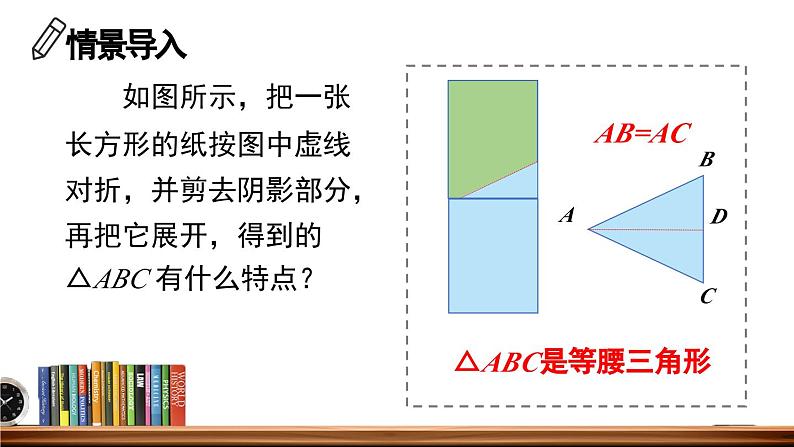
如图所示，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC 有什么特点？
（1）△ABC是轴对称图形吗？它的对称轴是什么？
等腰三角形是轴对称图形.
折痕所在的直线是它的对称轴.
（2）把剪出的△ABC沿折痕AD对折，找出其中能重合的线段和角，填入下表：
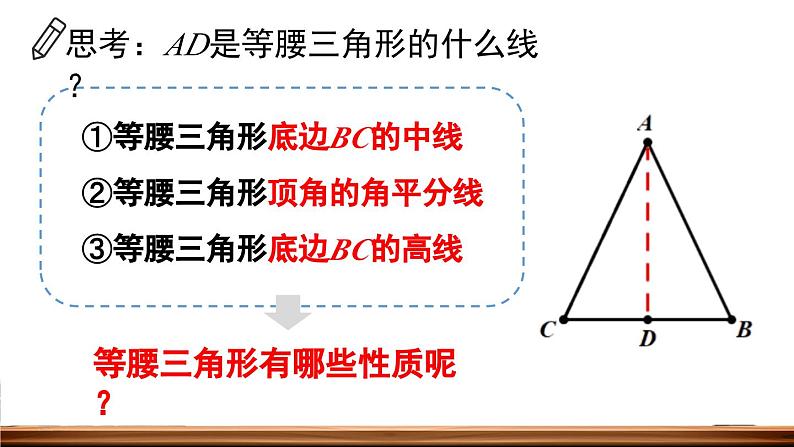
思考：AD是等腰三角形的什么线？
①等腰三角形底边BC的中线
②等腰三角形顶角的角平分线
③等腰三角形底边BC的高线
等腰三角形有哪些性质呢？
【性质1】等腰三角形的两个底角相等(简写成“等边对等角”)；【性质2】等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”)．
我们可以发现等腰三角形的性质:
怎么证明等腰三角形的性质呢？
已知：如图，△ABC 中，AB =AC （1） 求证：∠B=∠C
证明：作底边BC的中线AD.
∵ BD =CD， ∴在△BAD 和△CAD中△BAD ≌△CAD（SSS）．∴　∠B =∠C．
已知：如图，△ABC 中，AB =AC （2） 求证：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
证明：由（1）可知△BAD ≌△CAD （SSS） ∴∠ADB=∠ADC=90° ∠BAD=∠CAD ∴AD⊥BC，AD平分∠BAC由（1）可知AD是BC边的中线，∴AD是底边BC的高，也是底边BC的中线，也是顶角∠A的角平分线.
1.如图，AB∥CD，点E在AD上，AB=AE，∠B=70°，则∠D的度数为________.2.如图，在△ABC中，点D在边BC上，AB=AD=CD，∠BAD=40°，则∠C=____.
解： ∵ AB =AC，BD=BC=AD，∴∠ABC=∠C=∠BDC，∠A=∠ABD(等边对等角)设∠A=x，则∠BDC=∠A+∠ABD=2x，从而∠ABC=∠C=∠BDC=2x，于是在△ABC 中，有∠A +∠ABC+∠C =x+2x+2x =180°解得x=36°.所以，在△ABC中，∠A=36°，∠ABC=∠C =72°
如图，在△ABC 中，AB =AC，点 D 在 AC 上，且 BD =BC =AD．求△ABC 各角的度数．
1.在下列等腰三角形中，分别求出它们的底角的度数.
【课本P77 练习 第1题】
(180°－36°)÷2=72°
(180°－120°)÷2=30°
2. 如图，△ABC是等腰直角三角形（AB=AC，∠BAC=90°）， AD 是底边 BC上的高. 标出∠B，∠C，∠BAD，∠DAC 的度数，并写出图中所有相等的线段.
【课本P77 练习 第2题】
解：∵AB=AC，∠BAC=90°∴∠B=∠C=45°∵AD是BC边上的高，∴AD⊥BC∴AD是∠BAC的平分线∴∠BAD=∠DAC=45°.图中相等的线段有 BD=CD=AD，AB=AC
3.如图，在△ABC中，AB=AD=DC，∠BAD=26°求∠B和∠C的度数.
4. 如图，在△ABC中，AD平分∠BAC，AD=AC=BD，求∠B的度数.
解：∵AD平分∠BAC，∴∠BAD=∠CAD.∵AD=AC，∴∠ADC=∠C.∵AD=BD，∴∠BAD=∠B.设∠B=x，则∠BAC=2∠BAD=2x，∠C=∠ADC=∠B+∠BAD=2x，∴∠B+∠BAC+∠C=x+2x+2x=180°，解得x=36°，∴∠B=36°.
4.如图，在△ABC中，AB＝AC，E在CA的延长线上，∠AEF＝∠AFE，求证：EF⊥ BC.
证明：作AD⊥BC，垂足为D.∵AB=AC，∴∠BAC=2∠CAD.∵∠AEF=∠AFE，∴∠BAC=∠AEF+∠AFE=2∠AEF.∴∠CAD=∠AEF，∴AD∥EF.∵AD⊥BC，∴EF⊥BC.