数学八年级上册第十一章 三角形11.2 与三角形有关的角11.2.2 三角形的外角背景图ppt课件

这是一份数学八年级上册第十一章 三角形11.2 与三角形有关的角11.2.2 三角形的外角背景图ppt课件，共23页。PPT课件主要包含了99°，36°，三角形的外角的性质，教材P15练习，三角形的外角，三角形的外角和等内容，欢迎下载使用。
1.理解并掌握三角形的外角的概念.2.能够在复杂图形中找出外角.（难点）3.掌握三角形的外角的性质.（重点）4.会利用三角形的外角性质解决问题.（难点）
在△ABC 中，∠A = 80°， ∠B = 52°， 则 ∠C = _____.
3. 什么是三角形的内角？其内角和等于多少？
2. 如图，在△ABC 中，∠A = 70°，∠B = 60°， 则∠ACB = _____.
三角形相邻两边组成的角叫作三角形的内角.
三角形的内角和是 180 °.
如图，把△ABC 的一边 BC 延长，得到∠ACD，像这样，三角形的一边与另一边的延长线组成的角，叫做三角形的外角.
∠ACD 是 △ABC 的一个外角
三角形的外角的三个特征：1.顶点在三角形的一个顶点上；2.一条边是三角形的一条边；3.另一条边是三角形的某条边的延长线.
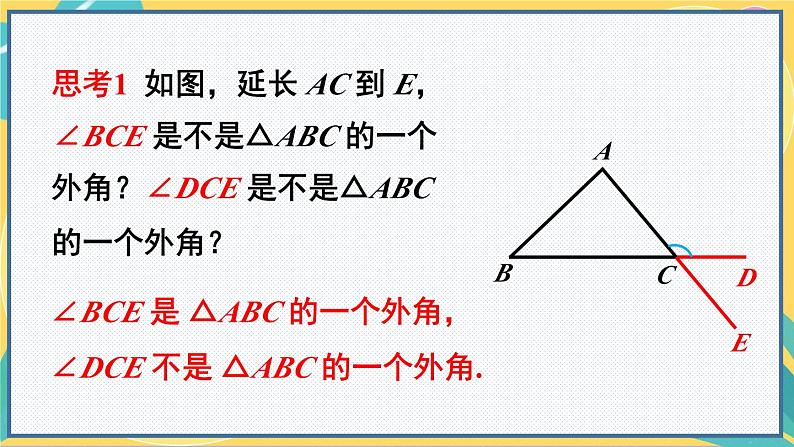
思考1 如图，延长 AC 到 E，∠BCE 是不是△ABC 的一个外角？∠DCE 是不是△ABC 的一个外角？
∠BCE 是 △ABC 的一个外角，∠DCE 不是 △ABC 的一个外角.
思考2 如图，∠ACD 与∠BCE 有什么关系？在三角形的每个顶点处有多少个外角？
∠ACD 与∠BCE 为对顶角，∠ACD = ∠BCE；
在三角形每个顶点处都有两个外角.
思考3 画出△ABC 的所有外角，共有几个呢？
每一个三角形都有 6 个外角．
每一个顶点相对应的外角都有 2 个，且这 2 个角为对顶角.
1. 如图，下列各角是△ABC 的外角的是（ ） A. ∠4 B. ∠3 C. ∠2 D. ∠1
2. 若三角形的一个外角等于和它相邻的内角， 则这个三角形是（ ） A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 都有可能
3. 如图，∠BEC 是哪个三角形的外角？∠AEC 是哪个 三角形的外角？∠EFD 是哪个三角形的外角？
∠BEC是△AEC 的外角;
∠AEC是△BEC 的外角;
∠EFD是△BEF 和△DCF的外角.
　　在△ABC 中，∠A = 70°，∠B = 60°， ∠ACD 是 △ABC 的一个外角，你能求出∠ACD 的度数吗？ ∠ACD 与 ∠A，∠B 的大小有什么关系？
∠ACD = ∠A +∠B
　　改变∠A ，∠B 的度数， ∠ACD 与 ∠A，∠B 还有你发现的关系吗？如果有，请说明理由并试着用语言归纳一下你发现的结论.
如图，任意一个△ABC 的外角∠ACD 与其不相邻的两内角（ ∠A，∠B ）有什么关系？
∵∠A + ∠B + ∠ACB = 180°，∠ACD + ∠ACB = 180°，∴∠A + ∠B = ∠ACD.
已知：如图△ABC，求证：∠ACD =∠A + ∠B.
证明：过 C 作 CE 平行于 AB，
∴∠2 = ∠B，（两直线平行，同位角相等）
∠1 = ∠A ， （两直线平行，内错角相等）
∴∠ACD = ∠1 + ∠2 = ∠A + ∠B.
三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
符号语言：∵ ∠ACD是△ABC 的一个外角，∴ ∠ACD = ∠A + ∠B.
1. 说出下列图形中 ∠1 和∠2 的度数：
∠1 = 40 °，∠2 = 140 °.
2. 如图，∠A = 42°，∠ABD = 28°，∠ACE = 18°， 求∠BFC 的度数.
解：∵ ∠BEC是△AEC 的一个外角，
∴ ∠BEC = ∠A + ∠ACE，
∵∠A = 42° ，∠ACE = 18°，
∴ ∠BEC =60°.
∵ ∠BFC 是△BEF 的一个外角，
∴ ∠BFC = ∠ABD + ∠BEF，
∵ ∠ABD = 28° ，∠BEC = 60°，
∴ ∠BFC = 88°.
例 4 如图， ∠BAE，∠CBF，∠ACD 是 △ ABC 的三个外角，它 们的和是多少？
解： ∵∠BAE = ∠2 + ∠3， ∠CBF = ∠1 +∠3， ∠ACD = ∠1 +∠2，∴∠BAE + ∠CBF +∠ACD = 2(∠1 +∠2 +∠3) = 2×180° = 360°.
解法二：如图，∠BAE + ∠1 = 180 ° ① ， ∠CBF +∠2 = 180 ° ②，∠ACD +∠3 = 180 ° ③，又知∠1 + ∠2 + ∠3 = 180 °，① + ② + ③ 得∠BAE + ∠CBF + ∠ACD+ (∠1+ ∠2+ ∠3) = 540 °，所以∠BAE + ∠CBF + ∠ACD = 540 °-180°= 360°.
解法三：过 A 作 AM 平行于 BC，
∠ACD ＝ ∠EAM，
∠CBF ＝ ∠BAM，
所以 ∠BAE＋ ∠CBF＋ ∠ACD＝ ∠BAE＋ ∠BAM＋ ∠EAM = 360°.
说出下列图形中∠1 和 ∠2 的度数：
∠1 = 40°，∠2 = 140°.
∠1 = 110°，∠2 = 70°.
∠1 = 50°，∠2 = 140°.
三角形的一边与另一边的延长线组成的角，叫做三角形的外角.
三角形的一个外角等于与它不相邻的两个内角的和
三角形的外角和等于360 °.