人教版八年级上册12.3 角的平分线的性质说课课件ppt

这是一份人教版八年级上册12.3 角的平分线的性质说课课件ppt，共17页。PPT课件主要包含了角平分线的性质探究等内容，欢迎下载使用。
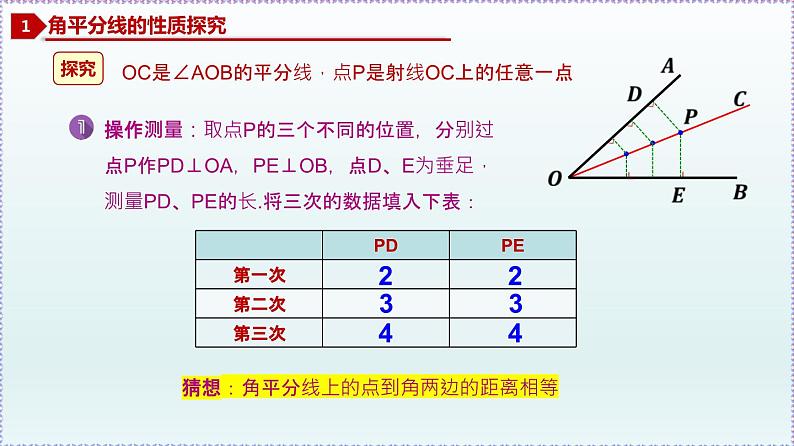
OC是∠AOB的平分线，点P是射线OC上的任意一点
操作测量：取点P的三个不同的位置，分别过点P作PD⊥OA，PE⊥OB，点D、E为垂足，测量PD、PE的长.将三次的数据填入下表：
猜想：角平分线上的点到角两边的距离相等
角平分线上的点到角两边距离相等
如图，已知∠AOC=∠BOC，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为D、E.求证：PD=PE.
∵PD⊥OA，PE⊥OB，
∴∠PDO=∠PEO=90°.
在ΔPDO和ΔPEO中，有
∴ ΔPDO ≌ ΔPEO(AAS)
一般情况下，证明一个几何问题可以参照如下步骤：
根据题意，画出图形，用数学符号表示已知和求证
明确问题中的已知和求证
通过分析，写出证明过程，证明结论
角平分线上的点到角两边的距离相等.
到角两边的距离相等的点在角平分线上.
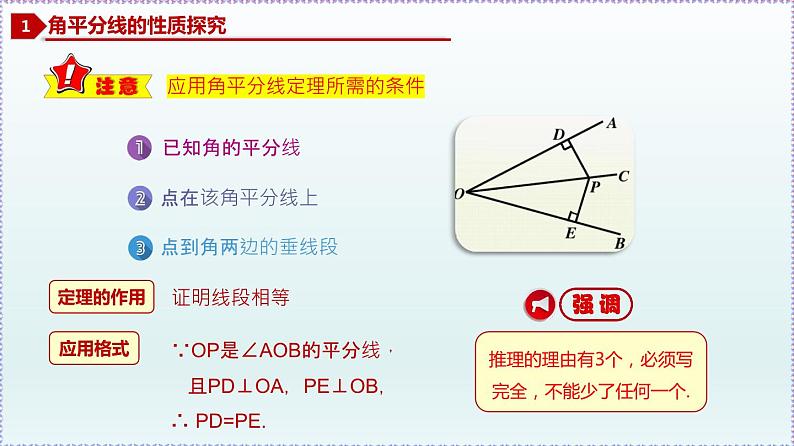
应用角平分线定理所需的条件
∵OP是∠AOB的平分线， 且PD⊥OA，PE⊥OB，
推理的理由有3个，必须写完全，不能少了任何一个.
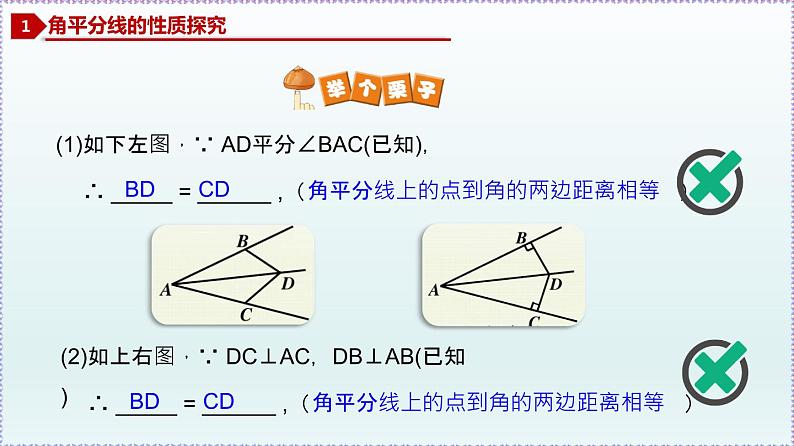
(1)如下左图，∵ AD平分∠BAC(已知)，
∴ _____ = ______ ,（ ）
BD CD
角平分线上的点到角的两边距离相等
(2)如上右图，∵ DC⊥AC，DB⊥AB(已知)
存在角平分线涉及距离问题
利用角平分线性质所得到的等量关系进行转化求解
如图，在△ABC中，AD是它的角平分线，且BD=CD，DE⊥AB，DF⊥AC，垂足分别为E，F.求证：EB=FC.
∵AD是∠BAC的平分线，DE⊥AB，DF⊥AC，
∴DE=DF，∠DEB=∠DFC=90°.
在RtΔBDE和RtΔCDF中，有
∴ RtΔBDE≌RtΔCDF(HL)
如图，AM是∠BAC的平分线，点P在AM上，PD⊥AB，PE⊥AC，垂足分别是D，E.PD=4，则PE= _______.
存在两条垂线段——直接应用
如图，在Rt△ABC中，AC=BC,∠C=90°，AP平分∠BAC，交BC与点P，若PC=4，AB=14.
(1)点P到AB的距离是_______
(2)求△APB的面积
由垂直平分线的性质，可知 PD=PC=4，
(1)如图，DE⊥AB，DF⊥BG，垂足分别是E，F，DE=DF，∠DEB=60°，则∠EBF=_____度.BE=_______.
(2)如图，△ABC中，∠C=90°，AD平分∠CAB，且BC=8，BD=5，则点D到AB的距离是______
用尺规作图作一个已知角的平分线的示意图如图所示，则能说明∠AOC=∠BOC的依据是（ ）
SSSASAAAS角平分线上的点到角两边距离相等