九年级中考数学复习 古老的传说1：将军饮马课件

这是一份九年级中考数学复习 古老的传说1：将军饮马课件，共26页。PPT课件主要包含了两定一动型，巩固练习，一定两动型，解决三角形周长问题，解决折线和问题，垂线段最短，两定两动型，综合拓展等内容，欢迎下载使用。
早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦.一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题. 将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它.从此以后，这个被称为“将军饮马”的问题便流传至今.
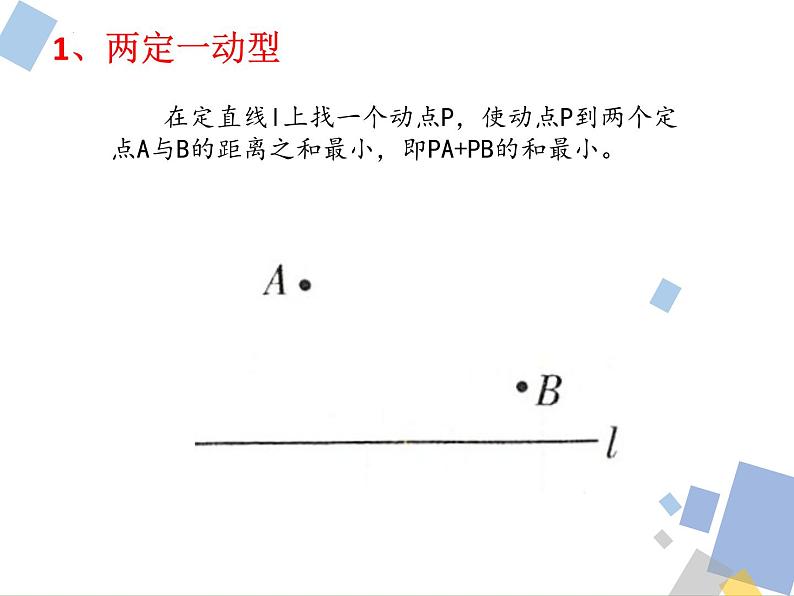
在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB的和最小。
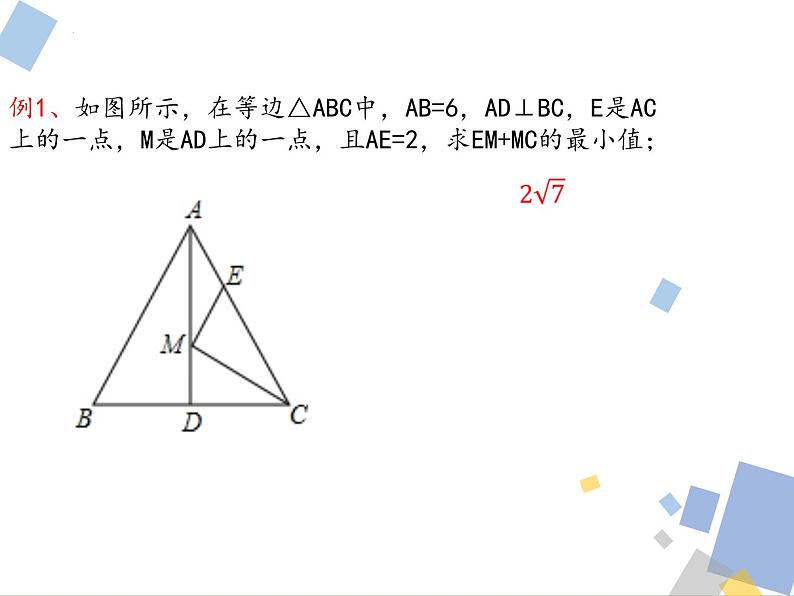
例1、如图所示，在等边△ABC中，AB=6，AD⊥BC，E是AC上的一点，M是AD上的一点，且AE=2，求EM+MC的最小值；
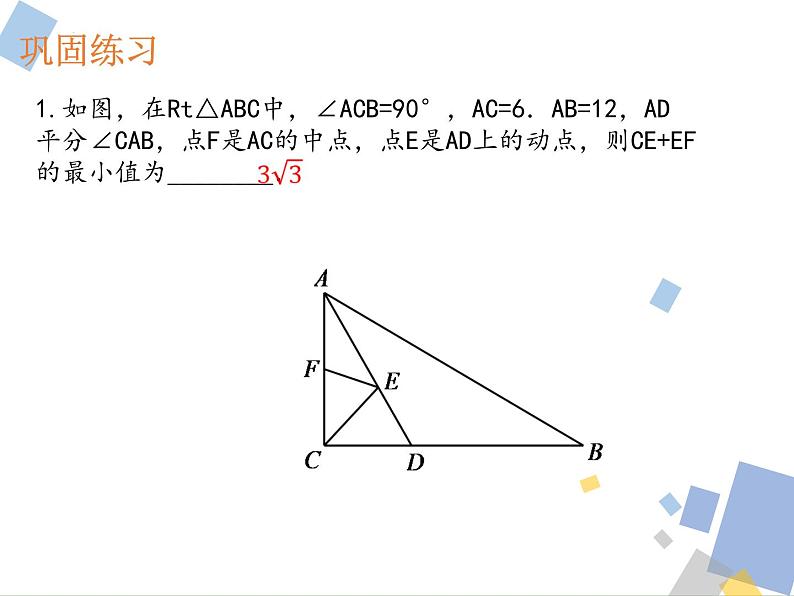
1.如图，在Rt△ABC中，∠ACB=90°，AC=6．AB=12，AD平分∠CAB，点F是AC的中点，点E是AD上的动点，则CE+EF的最小值为________．
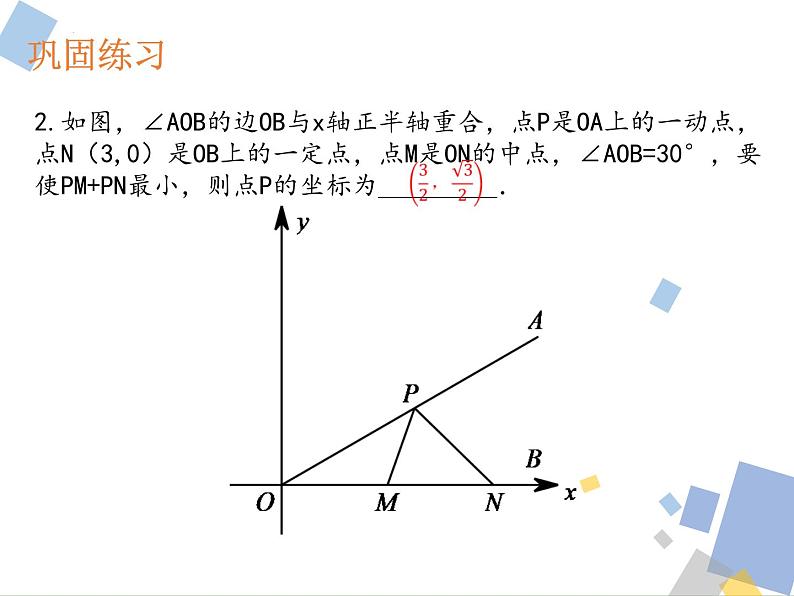
2.如图，∠AOB的边OB与x轴正半轴重合，点P是OA上的一动点，点N（3,0）是OB上的一定点，点M是ON的中点，∠AOB=30°，要使PM+PN最小，则点P的坐标为_________．
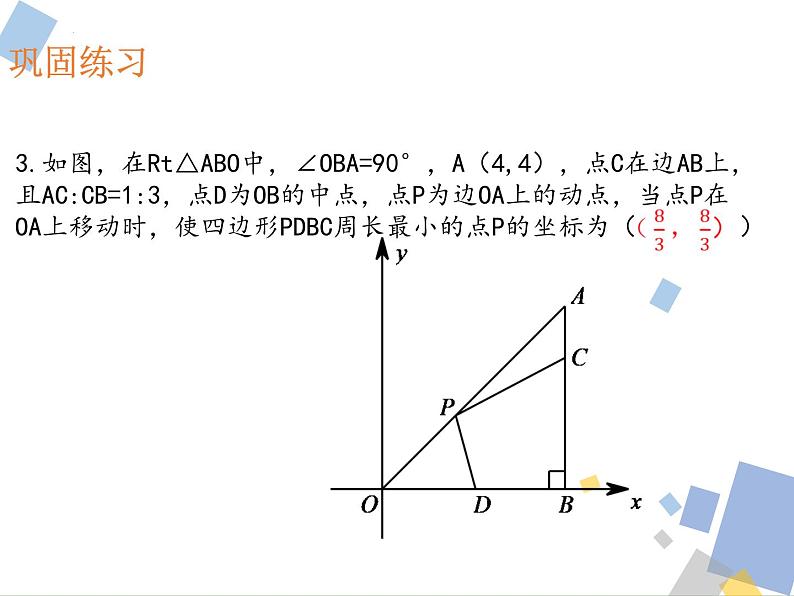
3.如图，在Rt△ABO中，∠OBA=90°，A（4,4），点C在边AB上，且AC:CB=1:3，点D为OB的中点，点P为边OA上的动点，当点P在OA上移动时，使四边形PDBC周长最小的点P的坐标为（       ）
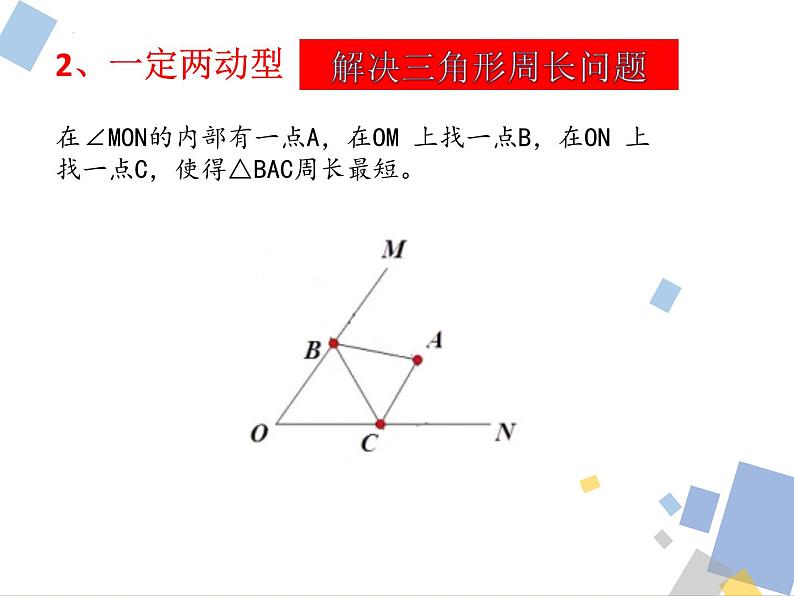
在∠MON的内部有一点A，在OM 上找一点B，在ON 上找一点C，使得△BAC周长最短。
例2、如图，点P是∠AOB内任意一点，∠AOB=30°，OP=8，点M和点N分别是射线OA和射线OB上的动点，则△PMN周长的最小值为________．
2、（2015•兰州）如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为（　　）
A是锐角∠MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使AB+BC值最小.(如图所示)
1、如图,矩形ABCD中，BC=10，∠BAC=30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，求这个最小值_________.
2.如图，在锐角三角形ABC中，BC=4，∠ABC=60°， BD平分∠ABC，交AC于点D，M、N分别是BD，BC上的动点，则CM+MN的最小值是________．
（二）（造桥选址）将军每日需骑马从军营出发，去河岸对侧的瞭望台观察敌情，已知河流的宽度为30米，请问，在何地修浮桥，可使得将军每日的行程最短？
例3、如图，当四边形PABN的周长最小时，a=___.
在平面直角坐标系中，有定点A(4,5),B(8,3)（1）若点C、D分别是x轴、y轴上的动点，求四边形ABCD的周长的最小值.（2）若C是y轴正半轴上的动点，延长OC至点D，使CD=3，当四边形ABCD的周长最短时，求点C的坐标.
1.如图，在l上找一点P，使｜PA-PB｜最大；
2、如图，在等边△ABC中，AB=4，P、M、N分别是BC、CA、AB边上动点，（1）求PM+MN的最小值；（2）求△PMN的周长最小值；
变式2、如图，已知Rt△ABC中，∠B＝90°，AB＝3，BC＝4，D、E、F分别是边AB、BC、AC上的动点，则DE+EF+FD的最小值为（　　）
3.如图，矩形ABOC的顶点A的坐标为（-4,5），D是OB的中点，E是OC上的一点，当△ADE的周长最小时，点E的坐标是__________．
4.如图，在矩形ABCD中，AB=6，AD=3，动点P满足△APB的面积是矩形ABCD面积的三分之一，则点P到A、B两点距离之和PA+PB的最小值为_________．