九年级中考数学一轮复习 考点讲练课件 ：微专题6　与正方形有关的常考模型

这是一份九年级中考数学一轮复习 考点讲练课件 ：微专题6　与正方形有关的常考模型，共24页。PPT课件主要包含了正方形中的半角模型等内容，欢迎下载使用。
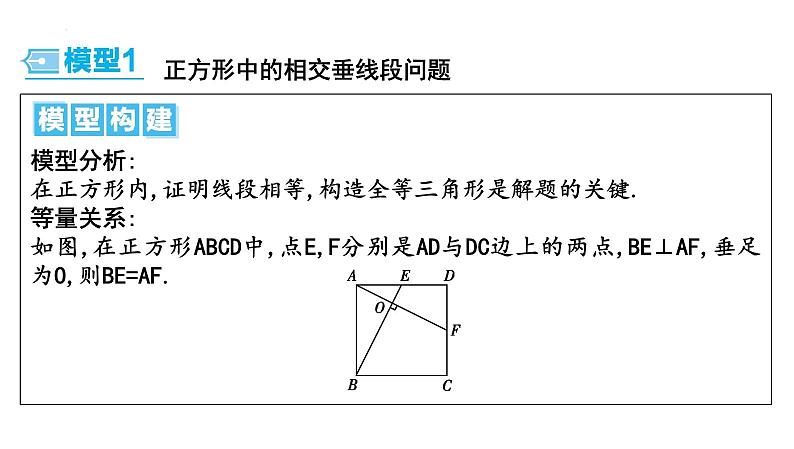
正方形中的相交垂线段问题
模型分析:在正方形内,证明线段相等,构造全等三角形是解题的关键.等量关系:如图,在正方形ABCD中,点E,F分别是AD与DC边上的两点,BE⊥AF,垂足为O,则BE=AF.
图形演变:在正方形内,分别连接两组对边上任意两点,得到的两条线段[如:图(1)中的线段AF与BE,图(2)中的线段AF与EG,图(3)中的线段HF与EG]满足:若垂直,则相等;若相等,则垂直.
[图(2)思路:过点B作BM∥GE交AD于点M;图(3)思路:过点B作BM∥GE交AD于点M;过点A作AN∥HF交CD于点N]
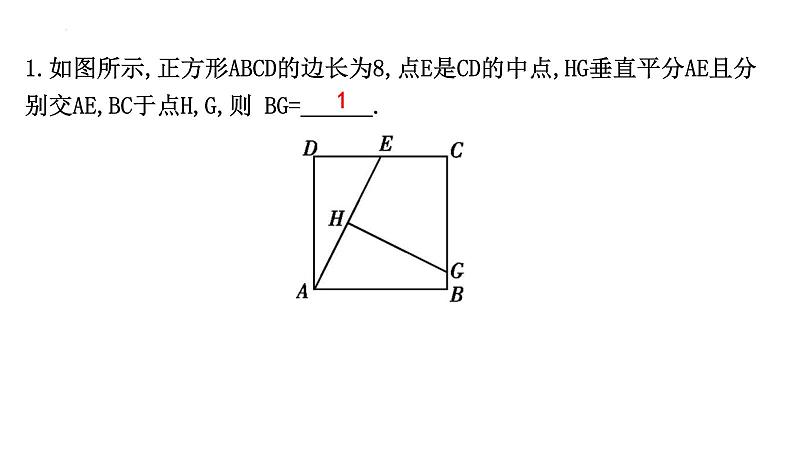
1.如图所示,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE,BC于点H,G,则 BG=　 　. 
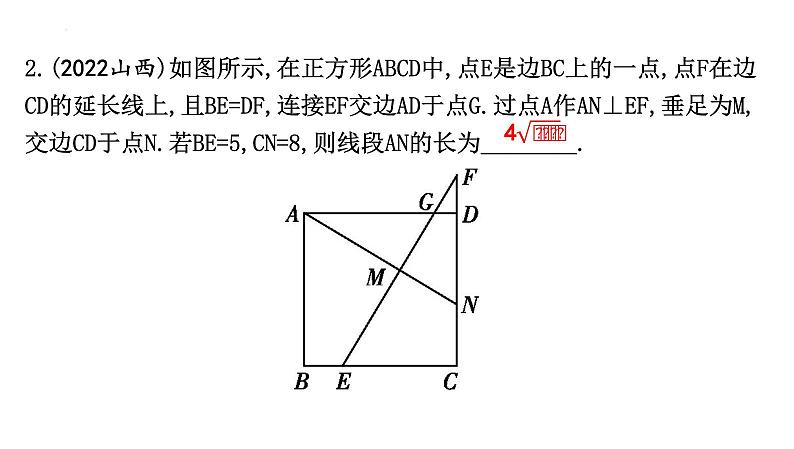
2.(2022山西)如图所示,在正方形ABCD中,点E是边BC上的一点,点F在边CD的延长线上,且BE=DF,连接EF交边AD于点G.过点A作AN⊥EF,垂足为M,交边CD于点N.若BE=5,CN=8,则线段AN的长为　 　. 
3.(2023绍兴)如图所示,在正方形ABCD中,点G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥BC,E,F分别为垂足.连接EF,AG,并延长AG交EF于点H.(1)求证:∠DAG=∠EGH;
(1)证明:在正方形ABCD中,AD⊥CD.又∵GE⊥CD,∴AD∥GE.∴∠DAG=∠EGH.
(2)判断AH与EF是否垂直,并说明理由.
(2)解:AH与EF垂直.理由如下:连接GC交EF于点O,如图所示.∵BD为正方形ABCD的对角线,∴∠ADG=∠CDG=45°.又∵DG=DG,AD=CD,∴△ADG≌△CDG.∴∠DAG=∠DCG.在正方形ABCD中,∠ECF=90°,又∵GE⊥CD,GF⊥BC,∴四边形FCEG为矩形.∴OE=OC.∴∠OEC=∠OCE.∴∠DAG=∠OEC.又∵∠DAG=∠EGH,∴∠EGH+∠GEH=∠OEC+∠GEH=∠GEC=90°.∴∠GHE=90°.∴AH⊥EF.
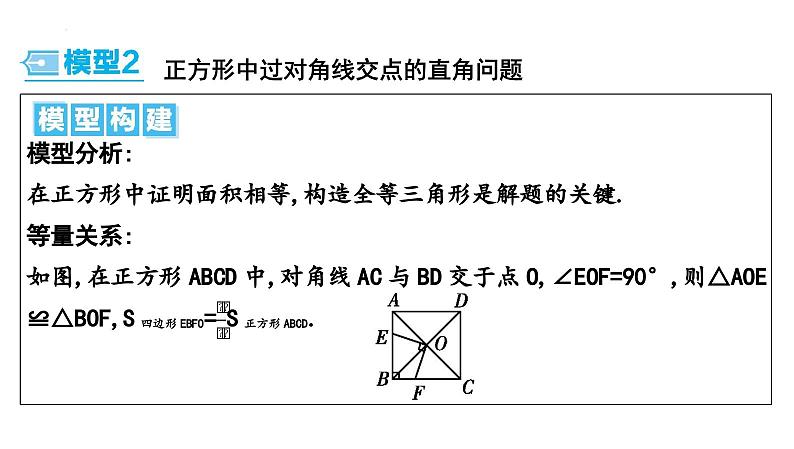
正方形中过对角线交点的直角问题
5.(2023海南一模)将一块足够大的直角三角板的直角顶点P放在边长为1的正方形ABCD的对角线AC上滑动,一条直角边始终经过点B,另一条直角边与射线DC交于点E.
(1)当点E在边DC上时,如图(1)所示,求证:①△PBC≌△PDC;②PB=PE.
(1)证明:①∵四边形ABCD是正方形,∴BC=CD,∠BCP=∠DCP=45°.又∵CP=CP,∴△PBC≌△PDC.
②过点P分别作PF⊥BC于点F,PG⊥CD于点G,如图所示.易证四边形PFCG为正方形,∴∠BFP=∠EGP=90°,PF=PG.∵∠EPG+∠EPF=90°=∠BPF+∠EPF,∴∠EPG=∠BPF.∴△PFB≌△PGE(ASA).∴PB=PE.
(2)当点E在边DC的延长线上时,如图(2)所示,则(1)中的结论②还成立吗?如果不成立,请说明理由;如果成立,请给予证明.
(2)解:PB=PE成立.证明如下:设PE交BC于点O,如图所示.∵∠BPE=∠BCE=90°,∠BOP=∠COE,∴∠PBC=∠PEC.由(1)得∠PBC=∠PDC,∴∠PDC=∠PEC.∴PE=PD.又∵PB=PD,∴PE=PB,故(1)中的结论②仍然成立.
正方形中的三垂直全等模型
模型分析:在正方形中,作垂线,构造全等三角形,作垂线是解决问题的关键.等量关系:如图,点E是正方形ABCD的边BC上一点,EF⊥AE于点E,FH⊥BH于点H,则△ABE≌△EHF
图形演变:(1)如图(1)所示,点G是正方形ABCD的边BC上一点,DE⊥AG于点E,BF⊥AG于点F,则△ADE≌△BAF;(2)如图(2)所示,直线l过正方形ABCD的顶点A,过点B,D分别作直线l的垂线,垂足分别为F,E,则△ADE≌△BAF;
(3)条件:四边形ABDC和四边形AEFG均为正方形,结论:△ABG≌△ACE,直线BG⊥CE.
模型分析:在正方形中,延长线段等于已知线段,通过证明三角形全等来证明一线段等于两线段的和,延长线段作辅助线是解决问题的关键.等量关系:如图所示,在正方形ABCD中,若∠EAF=45°,则EF=BF+DE.
图形演变:(1)如图所示,在正方形ABCD中,若∠EAF=45°,则:①EF=BE+DF;②△CEF的周长为正方形ABCD边长的2倍;③FA平分∠DFE,EA平分∠BEF;④MN2=BM2+DN2;(2)如图所示,在正方形ABCD中,若∠EAF=45°,FA平分∠DFE,则EF= DF-BE.
9.如图所示,点M,N分别在正方形ABCD的边BC,CD上,且 ∠MAN=45°.把△ADN绕点A顺时针旋转90°得到△ABE.(1)求证:△AEM≌△ANM;
(1)证明:由旋转的性质,得△ADN≌△ABE,∴∠DAN=∠BAE,AE=AN,∠D=∠ABE=90°.∴∠ABC+∠ABE=180°.∴点E,B,C三点共线.∵∠DAB=90°,∠MAN=45°,∴∠MAE=∠BAE+∠BAM=∠DAN+∠BAM=45°.∴∠MAE=∠MAN.又∵MA=MA,∴△AEM≌△ANM(SAS).