


中考数学一轮复习 课件 微专题2 六大全等模型
展开
这是一份中考数学一轮复习 课件 微专题2 六大全等模型,共34页。PPT课件主要包含了基础提升,cm或10cm,答图1,答图2等内容,欢迎下载使用。
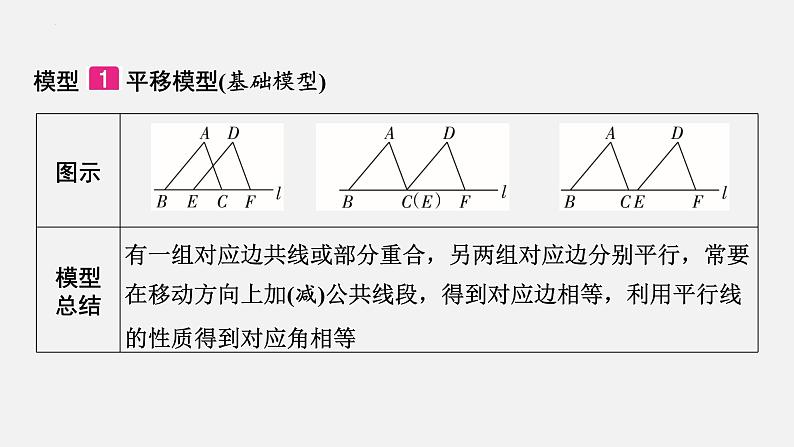
模型 平移模型(基础模型)
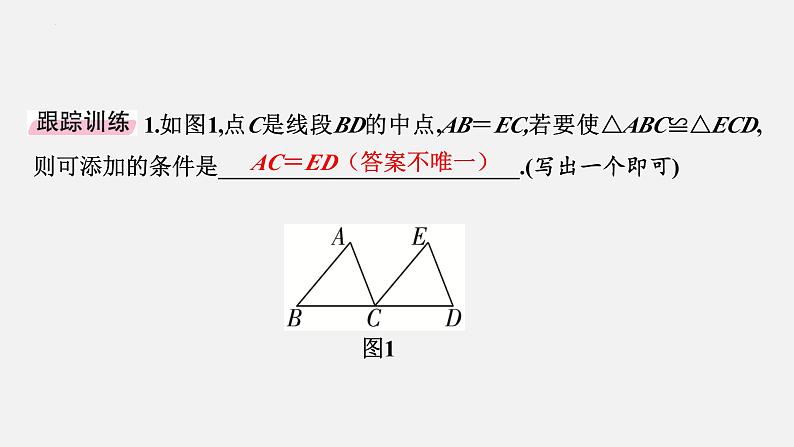
1.如图1,点C是线段BD的中点,AB=EC,若要使△ABC≌△ECD,则可添加的条件是__________________________.(写出一个即可)
AC=ED(答案不唯一)
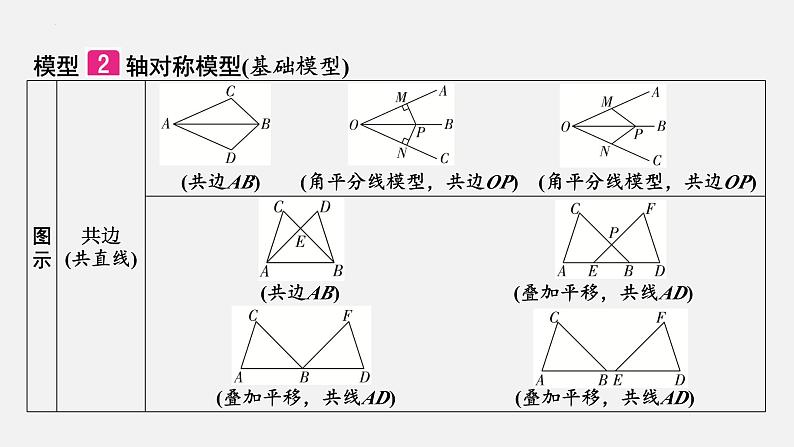
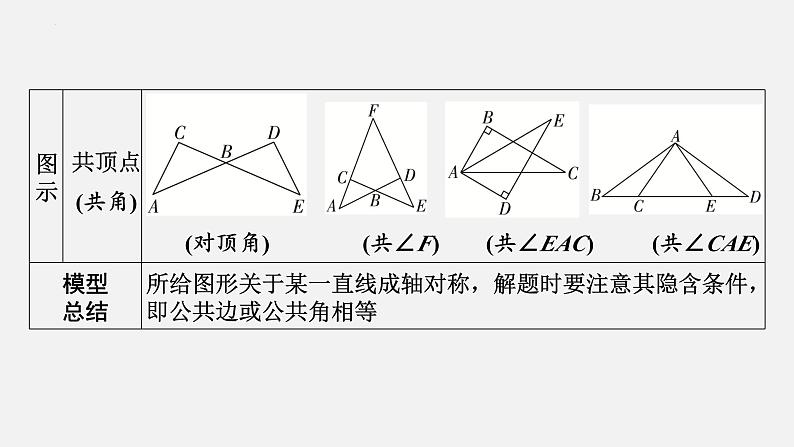
模型 轴对称模型(基础模型)
2.如图2,在△ABC中,∠BAC的平分线交BC于点D,E为AC上一点,AE=AB,连接DE.(1)求证:△ABD≌△AED;
证明:∵AD是∠BAC的平分线,∴∠BAD=∠EAD.
(2)已知AB=9,△CDE的周长为15,求△ABC的周长.
解:∵△ABD≌△AED,∴BD=DE.∴△CDE的周长为CD+DE+CE=CD+BD+CE=BC+CE=15.
又AE=AB=9,∴△ABC的周长为AB+BC+CA=AB+BC+CE+AE=9+15+9=33.
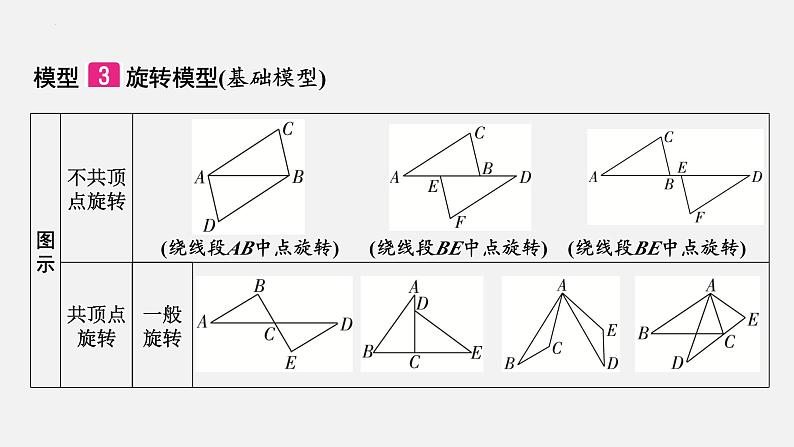
模型 旋转模型(基础模型)
3.(2023宜宾)已知:如图3,AB∥DE,AB=DE,AF=DC.求证:∠B=∠E.
证明:∵AF=DC,∴AF+CF=DC+CF,即AC=DF.∵AB∥DE,∴∠A=∠D.
模型 一线三等角模型(基础模型)
4.如图4,∠B=90°,△ABC≌△CDE,B,C,D三点共线.试说明:AC⊥CE.
证明:∵△ABC≌△CDE,∴∠D=∠B=90°,∠BCA=∠E.∴∠E+∠ECD=90°.∴∠BCA+∠ECD=90°.
∴∠ACE=180°-(∠BCA+∠ECD)=90°.∴AC⊥CE.
模型 对角互补模型(常见拓展模型)
5.如图5,在四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,求四边形ABCD的面积.
解:如答图1,过点A作AE⊥AC,交CB的延长线于点E.
∵∠DAB=∠DCB=90°,∴∠D+∠ABC=180°.
又∠ABE+∠ABC=180°,∴∠D=∠ABE.
∵∠DAB=∠CAE=90°,∴∠DAB-∠CAB=∠CAE-∠CAB,即∠CAD=∠EAB.
∴AE=AC=5,即△ACE是等腰直角三角形.
∵S四边形ABCD=S△ACD+S△ACB=S△AEB+S△ACB=S△ACE=12.5.∴四边形ABCD的面积为12.5.
模型 半角模型(常见拓展模型)
6.如图6,在正方形ABCD中,点M,N分别在边BC,CD上,且∠MAN=45°.将△ADN绕点A顺时针旋转90°得到△ABE.(1)求证:△AEM≌△ANM;
证明:由旋转的性质,得△ADN≌△ABE.
∴∠BAE=∠DAN,AE=AN,∠ABE=∠D=90°.∴∠ABC+∠ABE=180°.∴点E,B,C共线.
∵∠DAB=90°,∠MAN=45°,∴∠DAN+∠BAM=45°.∴∠BAE+∠BAM=45°,即∠MAE=45°.∴∠MAE=∠MAN.
(2)若BM=3,DN=2,求正方形ABCD的边长.
解:设CD=BC=x,则CM=x-3,CN=x-2,
∵△AEM≌△ANM,∴EM=NM.∵BE=DN,∴EM=NM=BM+DN=5.
∵∠C=90°,∴MN2=CM2+CN2,即25=(x-2)2+(x-3)2.解得x=6或-1(舍去).∴正方形ABCD的边长为6.
1.如图1,已知△DBC≌△ECB,且BE与CD相交于点A,下列结论错误的是( )A.BE=CD B.AB=AC C.∠D=∠E D.BD=AE
2.如图2,在△ABC中,∠C=90°,AC=10 cm,BC=5 cm,点P在线段AC上移动,点Q在与AC垂直的射线AM上移动,且PQ=AB,当AP=____________时,能使△ABC和△QPA全等.
3.如图3,已知AD=BE,BC=EF,AC=DF. 求证:△ABC≌△DEF.
证明:∵AD=BE,∴AD+BD=BE+BD,即AB=DE.
∴△ABC≌△DEF(SSS).
4.如图4,AD=BD,CD=ED,∠1=∠2,试证明∠3=∠1. 请按下列过程完成解答:(1)说明△ADE≌△BDC的理由;
解:∵∠1=∠2,∴∠1+∠BDE=∠2+∠BDE,即∠ADE=∠BDC.
∴△ADE≌△BDC(SAS).
(2)说明∠3=∠1的理由.
解:∵△ADE≌△BDC,∴∠AED=∠C. 又∠BED=∠2+∠C,即∠3+∠AED=∠2+∠C,∴∠3=∠2. ∵∠1=∠2,∴∠3=∠1.
5.如图5,已知点P(2m-1,6m-5)在第一象限的角平分线OC上.一直角的顶点与点P重合,角的两边与x轴、y轴分别交于点A,B.(1)求点P的坐标;
解:如答图1,过点P作PE⊥y轴于点E,PF⊥x轴于点F.∵点P在第一象限的角平分线OC上,∴PE=PF.∴2m-1=6m-5.解得m=1.∴点P的坐标为(1,1).
(2)求OA+OB的值.
解:由(1),得∠PEB=∠PFA=90°,∴∠EPF=90°.又∠BPA=90°,∴∠EPB+∠BPF=90°,∠FPA+∠BPF=90°.∴∠EPB=∠FPA.
∴△BEP≌△AFP(ASA).∴BE=AF.∴OA+OB=OF+AF+OE-BE=OF+OE.∵P(1,1),∴OE=OF=1.∴OA+OB=2.
6.(选做)如图6,在平面直角坐标系中,AB⊥x轴于点B,AC⊥y轴于点C,过点C作∠ECF分别交线段AB,OB于E,F两点,已知点A(4,4).(1)若OF+BE=AB,求证:CF=CE;
证明:∵AB⊥x轴,AC⊥y轴,∴∠ABO=∠ACO=90°.又∠BOC=90°,∴∠A=90°,即∠A=∠BOC.∵A(4,4),∴OC=AC=AB=4.
∵OF+BE=AB,AB=AE+BE,∴OF=AE.
∴△COF≌△CAE(SAS).∴CF=CE.
(2)若∠ECF=45°,S△ECF=6,求△BEF的面积.
解:如答图2,将△ACE绕点C顺时针旋转90°得到△OCG,∴CG=CE,∠ACE=∠OCG.∵∠ECF=45°,∴∠ACE+∠FCO=45°.∴∠GCF=∠OCG+∠FCO= ∠ACE+∠FCO=45°.∴∠GCF=∠ECF.
相关课件
这是一份中考数学第一轮复习 课件: 微专题8 全等三角形之六大模型,共43页。PPT课件主要包含了模型1平移模型,模型2对称模型,模型3旋转模型,模型4对角互补模型,模型6半角模型等内容,欢迎下载使用。
这是一份九年级中考数学一轮复习课件 微专题 五大常考全等模型,共32页。PPT课件主要包含了第1题图,第2题图,第3题图,第4题图,第5题图,第7题图,模型五半角模型,第8题图,第9题图等内容,欢迎下载使用。
这是一份中考数学一轮复习课件 微专题 全等三角形基本模型,共25页。









