中考数学一轮复习 课件 微专题3　全等三角形的常考模型

这是一份中考数学一轮复习 课件 微专题3　全等三角形的常考模型，共26页。PPT课件主要包含了平移型，对称型，旋转型，一线三等角型，倍长中线型，截长补短型，“手拉手”型，半角模型等内容，欢迎下载使用。
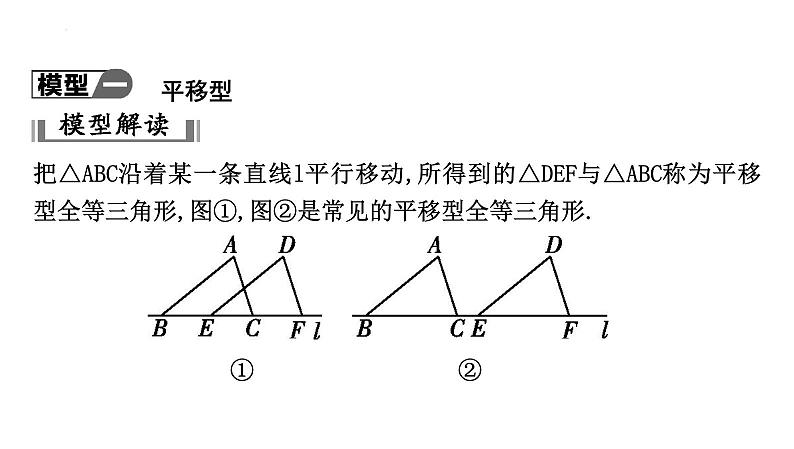
把△ABC沿着某一条直线l平行移动,所得到的△DEF与△ABC称为平移型全等三角形,图①,图②是常见的平移型全等三角形.
① ②
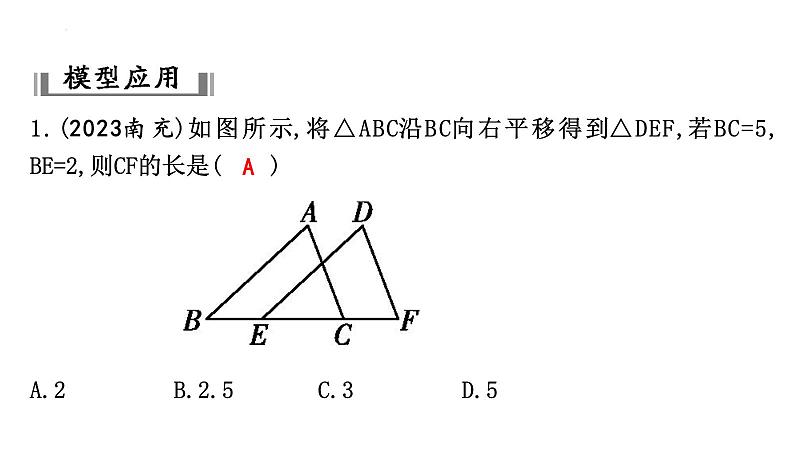
1.(2023南充)如图所示,将△ABC沿BC向右平移得到△DEF,若BC=5,BE=2,则CF的长是( )A.2B.2.5C.3D.5
2.(2022乐山)如图所示,B是线段AC的中点,AD∥BE,BD∥CE.求证:△ABD≌△BCE.
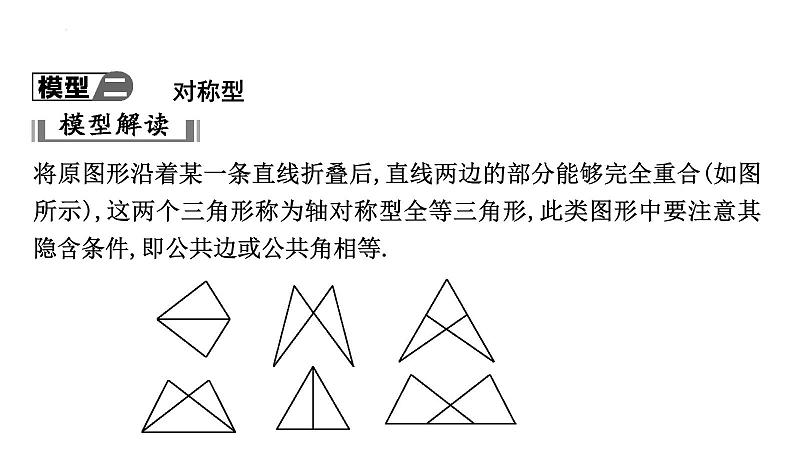
将原图形沿着某一条直线折叠后,直线两边的部分能够完全重合(如图所示),这两个三角形称为轴对称型全等三角形,此类图形中要注意其隐含条件,即公共边或公共角相等.
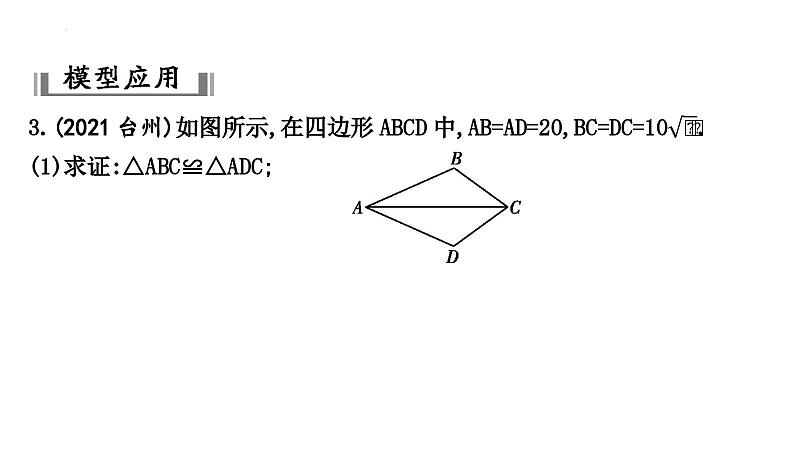
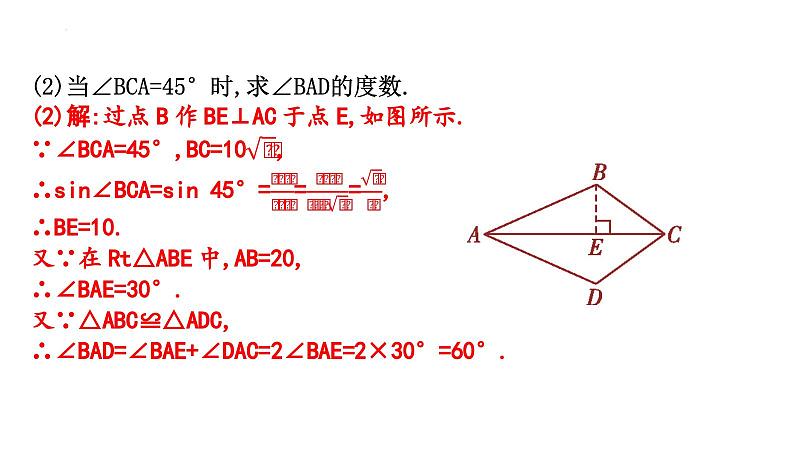
(2)当∠BCA=45°时,求∠BAD的度数.
将三角形绕着公共点旋转一定角度后,两个三角形能够完全重合(如图所示),则称这两个三角形为旋转型全等三角形,识别旋转型全等三角形时,涉及对顶角、等角加(减)公共角等条件.
4.(2023宜宾)如图所示,M是正方形ABCD边CD的中点,P是正方形内一 点,连结BP,线段BP以点B为中心逆时针旋转90°得到线段BQ,连结MQ.若AB=4,MP=1,则MQ的最小值为　 　. 
5.(2022碑林期中)如图所示,在△ABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BE=CF,BD=CE,∠A=30°,求∠DEF的度数.
中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线加长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.
6.如图所示,在正方形ABCD中,AB=6,E是BC边的中点,F是CD边上的一 点,且DF=2,若M,N分别是线段AD,AE上的动点,则MN+MF的最小值为　 　. 
截长补短的方法适用于求证线段的和差倍分关系.截长,指在长线段中截取一段等于已知线段;补短,指将短线段延长,延长部分等于已知线 段.该类题目中常出现等腰三角形、角平分线等.
7.(2022兰陵期中)如图所示,在△ABC中,∠1=∠2,∠B=2∠C,求证:AC=AB+BD.
∴△ABD≌△AED(),∴BD=ED,∠B=∠AED.∵∠B=2∠C,∴∠AED=2∠C.又∵∠AED=∠C+∠CDE,∴∠C=∠CDE,∴CE=DE,∴BD=CE,∴AC=AE+CE=AB+BD.
由两个等顶角的等腰三角形或正方形组成,并且顶角的顶点为公共顶点的模型.
8.(2022南昌期中)如图所示,△ABC,△DEF是两个全等的等边三角形,它们的一边都在直线l上,AC,DE交于点P.
(1)判断△PCE的形状,并说明理由;
(1)解:△PCE是等边三角形.理由如下:∵△ABC,△DEF是两个全等的等边三角形,且△ABC与△DEF全等,∴∠DEC=∠ACE=60°,∴∠EPC=180°-∠DEC-∠ACE=180°-60°-60°=60°,∴△PCE是等边三角形.
(2)写出图中所有与线段PA相等的线段,并说明理由;
(2)解:PD,CF,BE.理由如下:∵△ABC,△DEF,△PEC均是等边三角形,且△ABC与△DEF全等,∴AC=AB=BC=DE=DF=EF,PE=PC=EC,∴PA=PD=CF=BE.
(3)证明:AF=BD.
过等腰三角形的顶点引两条射线,使两条射线的夹角为顶角的一半.半角模型常见于正方形、等边三角形、等腰直角三角形中.常用于证明线段之间的数量关系.
9.(2022蚌埠月考)如图所示,已知正方形ABCD,从顶点A引两条射线分别交BC,CD于点E,F,且∠EAF=45°,求证:BE+DF=EF.