北师大版九年级上册3 正方形的性质与判定教学ppt课件

这是一份北师大版九年级上册3 正方形的性质与判定教学ppt课件，共22页。PPT课件主要包含了③④⑤，正方形的性质，·边·，·角·，·对角线·，四个角都是直角，对称性·，正方形的判定，定义法，对角线法等内容，欢迎下载使用。
1．掌握正方形的定义及性质，理解正方形与平行四边形、矩形、菱形的关系．
2．正确运用正方形的性质解题．
1.有一个内角是 的平行四边形是矩形.2.有一组 相等的平行四边形是菱形.3.下列性质中①对角相等②对边相等③对角互补④对角线相等⑤对角线互相平分⑥对角线互相垂直⑦一条对角线平分一组对角，矩形具有而一般的平行四边形不具有的性质是 ；菱形具有而一般的平行四边形不具有的性质是 .4.下列图形中既是中心对称图形又是轴对称图形的是 （把序号填在横线上）①等边三角形②平行四边形③矩形④线段⑤菱形⑥角.
四条边都相等，对边平行.
相等、互相垂直且平分、每条对角线平分一组对角
是轴对称图形，共有4条对称轴,也是中心对称图形.
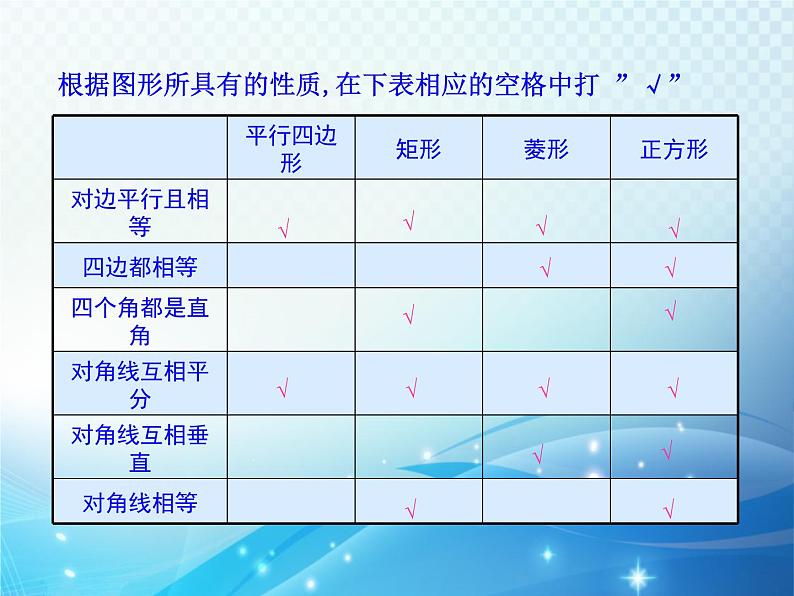
根据图形所具有的性质,在下表相应的空格中打 ”√”
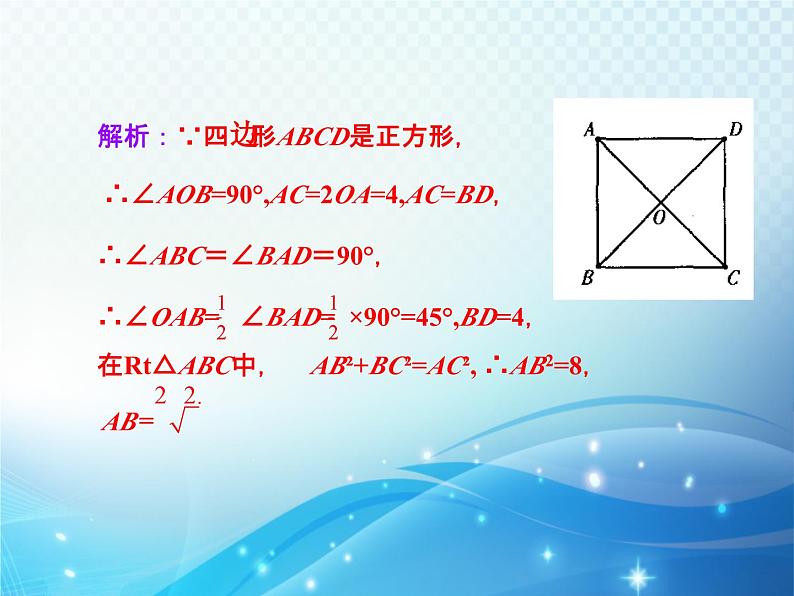
【例】如图，在正方形ABCD中，两条对角线相交于O点，OA=2，求∠AOB、∠OAB的度数及BD，AB的长.
解析：∵四边形ABCD是正方形，
∴∠ABC＝∠BAD＝90°，
∴∠AOB=90°,AC=2OA=4,AC=BD，
∴∠OAB= ∠BAD= ×90°=45°,BD=4，
在Rt△ABC中，　AB²+BC²=AC², ∴AB2=8，
①有一组邻边相等的平行四边形②四条边都相等的四边形③对角线互相垂直的平行四边形
①有一个角是直角的平行四边形②有三个角是直角的四边形③对角线相等的平行四边形
两条对角线互相垂直平分且相等的四边形是正方形.
有一组邻边相等的矩形是正方形.
有一个角是直角的菱形是正方形.
既是矩形又是菱形的四边形是正方形.
1.正方形具有而一般菱形不一定具有的性质是（ ）A.内角和为360° B.对角线平分内角C.对角线相等 D.对角线互相垂直平分2.正方形具有而一般矩形不一定具有的性质是（ ）A.对边平行且相等 B.对角线互相垂直C.对角线相等 D.四个角都是直角
3.正方形ABCD中，对角线的交点为O，E是OB上的一点，DG⊥AE于G,DG交OA于F.求证：OE=OF.
证明：在正方形ABCD中
OA=OD，∠AOD=∠AOE=90°，
∵∠ODF+∠DFO=90°，
∠FAG+∠AFG=90°，
∴∠ODF=∠FAG，
∴△DOF≌△AOE，
（1）下列判断中正确的是（ ） A.四边相等的四边形是正方形 B.四角相等的四边形是正方形 C.对角线垂直的平行四边形是正方形 D.对角线互相垂直平分且相等的四边形是正方形
（2）在四边形ABCD中O是对角线的交点，能判定这个四边形是正方形的是（ ） A.AC = BD，AB∥CD，AB=CD B.AD∥BC，∠A =∠C C.AO=BO=CO=DO，AC⊥BD D.AO=CO，BO=DO，AB=BC
（3）（晋江·中考）如图，将一张正方形纸片剪成四个小正方形，得到4个正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个正方形，称为第三次操作；...，根据以上操作，若要得到2 011个正方形，则需要操作的次数是( ) .
A.669 B. 670　C.671 D. 672
2.AC为正方形ABCD的对角线，E为AC上一点，且AB=AE，EF⊥AC交BC于F，求证：EC=EF=FB
证明：∵四边形ABCD是正方形, ∴∠B=90°,∠ACB=45°.
∴BF=EF.又∵∠FEC=90°,∴∠EFC=45°, ∴EC=EF（等角对等边）, ∴BF=EF=EC.
∵∠AEF=∠B =90°,AB=AE AF=AF ∴△ABF≌△AEF,
3.将一个菱形绕两条对角线的交点旋转90°，所得图形与原来的图形重合，此时的菱形是正方形吗？为什么？
解析：是正方形，此菱形的对角线相等
4.（青海·中考）如图，正方形ABCD的对角线AC和BD相交于点O，O又是正方形A1B1C1O的一个顶点，O A1交AB于点E，OC1交BC于点F.（1）求证：△AOE≌△BOF.（2）如果两个正方形的边长都为a，那么正方形A1B1C1O绕O点转动，两个正方形重叠部分的面积等于多少？为什么？
【解析】（1）在正方形ABCD中，AO=BO，∠AOB=90°，∠OAB=∠OBC=45°∵∠AOE+∠EOB=90°, ∠BOF+∠EOB=90°，∴∠AOE=∠BOF，在△AOE和△BOF中，
∴△AOE≌△BOF.
所以：S四边形OEBF=S△EOB+S△OBF= S△EOB+S△AOE=S△AOB=
因为△AOE≌△BOF，
(2)两个正方形重叠部分面积等于
（1）两组对边分别平行；（2）两组对边分别相等；（3）一组对边平行且相等；（4）两条对角线互相平分；（5）两组对角分别相等.
（1）有三个角是直角；（2）是平行四边形，并且有一个角是直角；（3）是平行四边形，并且两条对角线相等.
（1） 四条边都相等；（2）是平行四边形，并且有一组邻边相等；（3）是平行四边形，并且两条对角线互相垂直.
（1）是矩形，并且有一组邻边相等；（2）是菱形,并且有一个角是直角.