






还剩12页未读,
继续阅读
初中人教版第二十一章 一元二次方程21.2 解一元二次方程21.2.3 因式分解法教课课件ppt
展开
这是一份初中人教版第二十一章 一元二次方程21.2 解一元二次方程21.2.3 因式分解法教课课件ppt,共20页。PPT课件主要包含了获取新知,-49x0,x10,x2≈204,要点归纳,例1解下列方程,于是得,解化为一般式为,因式分解得等内容,欢迎下载使用。
1. 解一元二次方程的基本思路是什么?
直接开平方法,配方法,公式法.
2.我们已经学过哪些解一元二次方程的方法?
问题 根据物理学规律,如果把一个物体从地面以10m/s的速度竖直上抛,那么经过x s物体离地面的高度(单位:m)为10-4.9x2. 你能根据上述规律求出物体经过多少秒落回地面吗(精确到0.01s)?
解析:设物体经过 x s落回地面,这时它离地面的高度为0,即
10x-4.9x2=0 ①
尝试:用配方法或公式法解方程①.
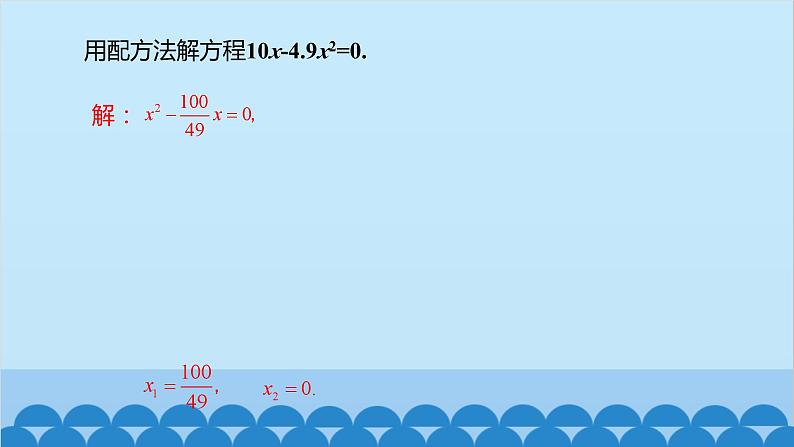
用配方法解方程10x-4.9x2=0.
用公式法解方程10x-4.9x2=0.
∵ a=4.9,b=-10,c=0.
∴ b2-4ac = (-10)2-4×4.9×0=100.
10x-4.9x2=0.
思考:除配方法或公式法以外,能否找到更简单的方法来解方程①?
两个因式乘积为 0,说明什么?
降次,化为两个一次方程
解两个一次方程,得出原方程的根
10x-4.9x2 =0
x(10-4.9x) =0
如果a · b = 0,那么 a = 0或 b = 0.
这两个根中, 表示物体约在2.04 s时落回地面;而 表示物体被上抛离开地面的时刻,即在0 s时物体被抛出,此刻物体的高度是0 m.
这种解法是不是很简单?
通过因式分解,使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解一元一次方程的方法叫做因式分解法.
一移——方程的右边=0;
二分——方程的左边因式分解;
三化——方程化为两个一元一次方程;
四解——写出方程两个解.
因式分解法解一元二次方程的基本步骤:
简记口诀:右化零,左分解,两因式,各求解.
解:(1)因式分解,得
x-2=0 或 x+1=0,
x1=2,x2=-1.
(x-2)(x+1)=0.
解:(2)移项、合并同类项,得
因式分解,得 ( 2x+1)( 2x-1 )=0.
2x+1=0或2x-1=0,
x2-2x+1 = 0.
x1 = x2 = 1.
例2 用适当的方法解方程:(1) 3x(x + 5)= 5(x + 5);
分析:该式左右两边可以提取公因式,所以用因式分解法解答较快.
解:化简 (3x -5) (x + 5) = 0.即 3x - 5 = 0 或 x + 5 = 0.
(2)(5x + 1)2 = 1;
分析:方程一边以平方形式出现,另一边是常数,可直接开平方法.
(3)x2 - 12x = 4 ;
分析:二次项的系数为1,可用配方法来解题较快.
解:配方,得 x2 - 12x + 62 = 4 + 62, 即 (x - 6)2 = 40. 开平方,得 解得
(4)3x2 = 4x + 1.
解:化为一般形式 3x2 - 4x + 1 = 0. ∵Δ=b2 - 4ac = 28 > 0,
分析:二次项的系数不为1,且不能直接开平方,也不能直接因式分解,所以适合公式法.
1.用因式分解法解下列方程:(1) x2-1=2(x+1)
解:(1)∵x2-1=2(x+1),∴(x+1)(x-1)-2(x+1)=0,∴(x+1)(x-1-2)=0,∴(x+1)(x-3)=0,∴x+1=0或x-3=0,解得x1=-1,x2=3.
(2)(x+3)2=(1-2x)2.
2.用适当的方法解下列方程:(1)(x-3)2-25=0;
解:(1)(x-3)2-25=0.移项,得(x-3)2=25.开平方,得x-3=±5,即x-3=5或x-3=-5,解得x1=8,x2=-2.
(2)(x-2)(x+1)=0,∴x-2=0或x+1=0,解得x1=2,x2=-1.
(3)移项,得x2+8x=-15.配方,得x2+8x+16=1,即(x+4)2=1.开平方,得x+4=±1,即x+4=1或x+4=-1,解得x1=-3,x2=-5.
(2)x(x-2)+x-2=0;(3)x2+8x+15=0.
1. 解一元二次方程的基本思路是什么?
直接开平方法,配方法,公式法.
2.我们已经学过哪些解一元二次方程的方法?
问题 根据物理学规律,如果把一个物体从地面以10m/s的速度竖直上抛,那么经过x s物体离地面的高度(单位:m)为10-4.9x2. 你能根据上述规律求出物体经过多少秒落回地面吗(精确到0.01s)?
解析:设物体经过 x s落回地面,这时它离地面的高度为0,即
10x-4.9x2=0 ①
尝试:用配方法或公式法解方程①.
用配方法解方程10x-4.9x2=0.
用公式法解方程10x-4.9x2=0.
∵ a=4.9,b=-10,c=0.
∴ b2-4ac = (-10)2-4×4.9×0=100.
10x-4.9x2=0.
思考:除配方法或公式法以外,能否找到更简单的方法来解方程①?
两个因式乘积为 0,说明什么?
降次,化为两个一次方程
解两个一次方程,得出原方程的根
10x-4.9x2 =0
x(10-4.9x) =0
如果a · b = 0,那么 a = 0或 b = 0.
这两个根中, 表示物体约在2.04 s时落回地面;而 表示物体被上抛离开地面的时刻,即在0 s时物体被抛出,此刻物体的高度是0 m.
这种解法是不是很简单?
通过因式分解,使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解一元一次方程的方法叫做因式分解法.
一移——方程的右边=0;
二分——方程的左边因式分解;
三化——方程化为两个一元一次方程;
四解——写出方程两个解.
因式分解法解一元二次方程的基本步骤:
简记口诀:右化零,左分解,两因式,各求解.
解:(1)因式分解,得
x-2=0 或 x+1=0,
x1=2,x2=-1.
(x-2)(x+1)=0.
解:(2)移项、合并同类项,得
因式分解,得 ( 2x+1)( 2x-1 )=0.
2x+1=0或2x-1=0,
x2-2x+1 = 0.
x1 = x2 = 1.
例2 用适当的方法解方程:(1) 3x(x + 5)= 5(x + 5);
分析:该式左右两边可以提取公因式,所以用因式分解法解答较快.
解:化简 (3x -5) (x + 5) = 0.即 3x - 5 = 0 或 x + 5 = 0.
(2)(5x + 1)2 = 1;
分析:方程一边以平方形式出现,另一边是常数,可直接开平方法.
(3)x2 - 12x = 4 ;
分析:二次项的系数为1,可用配方法来解题较快.
解:配方,得 x2 - 12x + 62 = 4 + 62, 即 (x - 6)2 = 40. 开平方,得 解得
(4)3x2 = 4x + 1.
解:化为一般形式 3x2 - 4x + 1 = 0. ∵Δ=b2 - 4ac = 28 > 0,
分析:二次项的系数不为1,且不能直接开平方,也不能直接因式分解,所以适合公式法.
1.用因式分解法解下列方程:(1) x2-1=2(x+1)
解:(1)∵x2-1=2(x+1),∴(x+1)(x-1)-2(x+1)=0,∴(x+1)(x-1-2)=0,∴(x+1)(x-3)=0,∴x+1=0或x-3=0,解得x1=-1,x2=3.
(2)(x+3)2=(1-2x)2.
2.用适当的方法解下列方程:(1)(x-3)2-25=0;
解:(1)(x-3)2-25=0.移项,得(x-3)2=25.开平方,得x-3=±5,即x-3=5或x-3=-5,解得x1=8,x2=-2.
(2)(x-2)(x+1)=0,∴x-2=0或x+1=0,解得x1=2,x2=-1.
(3)移项,得x2+8x=-15.配方,得x2+8x+16=1,即(x+4)2=1.开平方,得x+4=±1,即x+4=1或x+4=-1,解得x1=-3,x2=-5.
(2)x(x-2)+x-2=0;(3)x2+8x+15=0.













