



所属成套资源:2024高考数学一轮题型分类细讲精练
2024一轮题型分类细讲精练02:常用逻辑用语
展开
这是一份2024一轮题型分类细讲精练02:常用逻辑用语,文件包含解密02常用逻辑用语原卷版docx、解密02常用逻辑用语解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
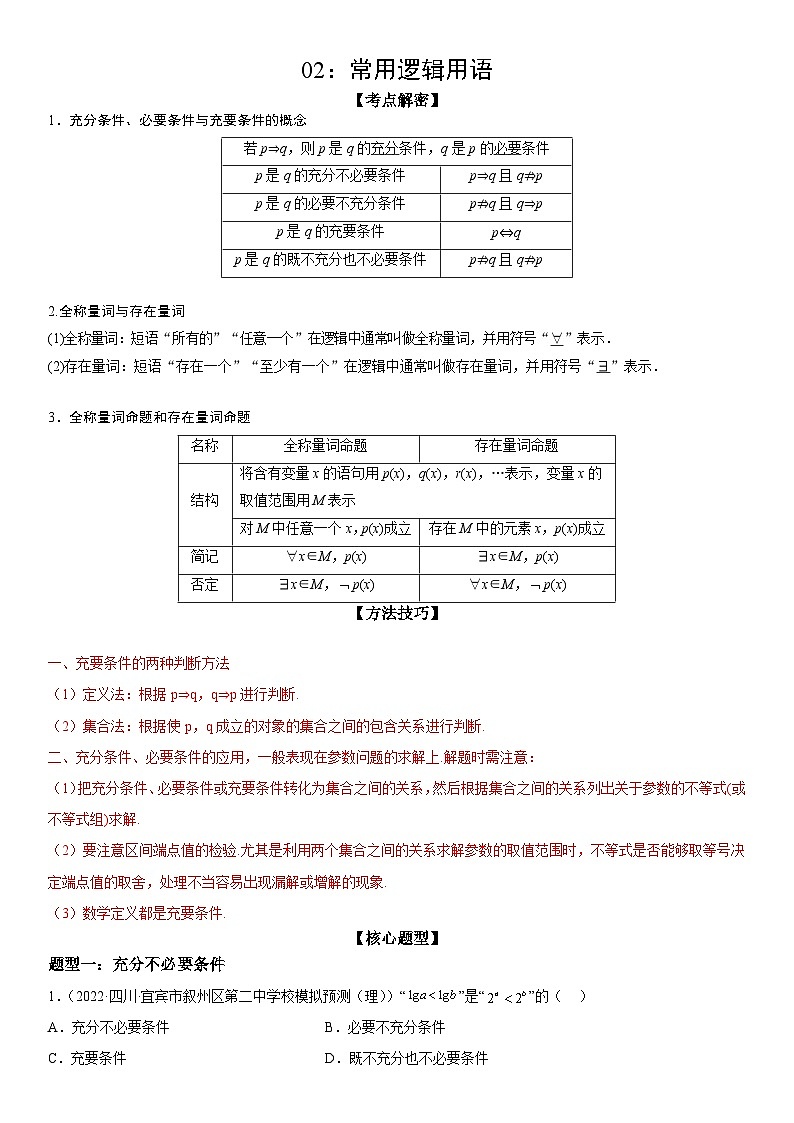
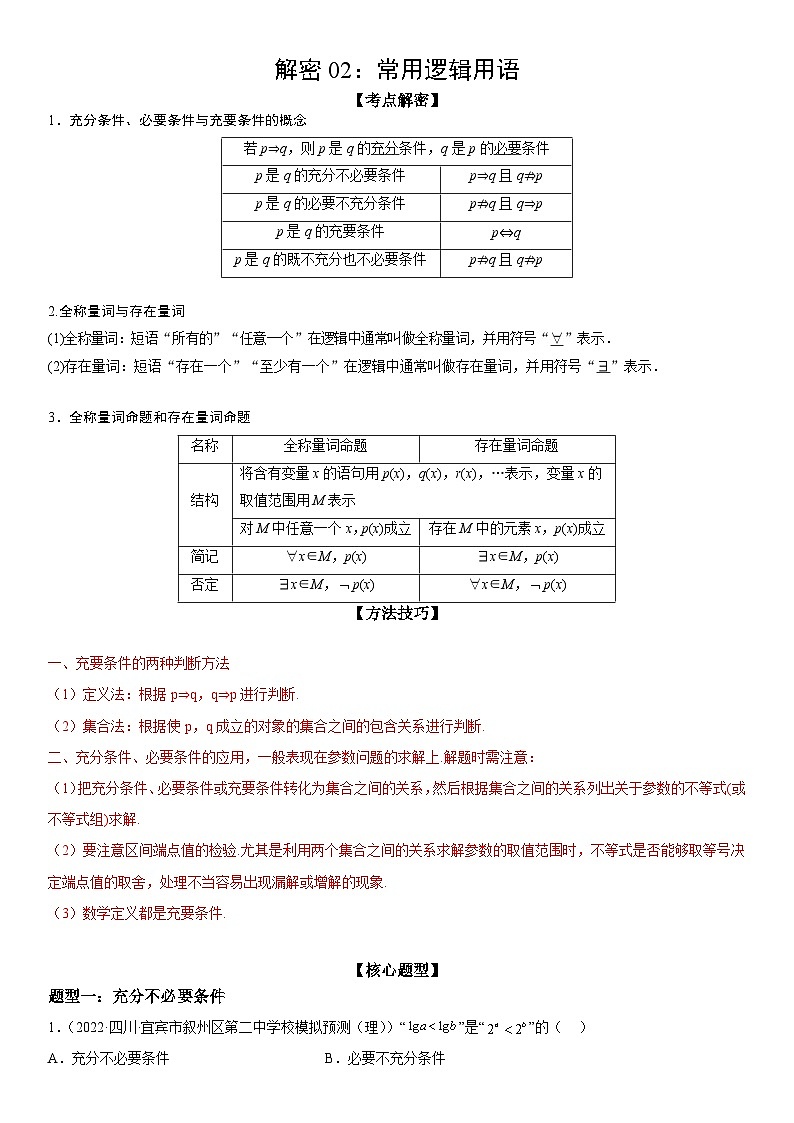
1.充分条件、必要条件与充要条件的概念
2.全称量词与存在量词
(1)全称量词:短语“所有的”“任意一个”在逻辑中通常叫做全称量词,并用符号“∀”表示.
(2)存在量词:短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,并用符号“∃”表示.
3.全称量词命题和存在量词命题
【方法技巧】
一、充要条件的两种判断方法
(1)定义法:根据p⇒q,q⇒p进行判断.
(2)集合法:根据使p,q成立的对象的集合之间的包含关系进行判断.
二、充分条件、必要条件的应用,一般表现在参数问题的求解上.解题时需注意:
(1)把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.
(2)要注意区间端点值的检验.尤其是利用两个集合之间的关系求解参数的取值范围时,不等式是否能够取等号决定端点值的取舍,处理不当容易出现漏解或增解的现象.
(3)数学定义都是充要条件.
【核心题型】
题型一:充分不必要条件
1.(2022·四川·宜宾市叙州区第二中学校模拟预测(理))“”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
2.(2022·山东济南·模拟预测)设:,:,则是成立的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
3.(2022·四川资阳·一模(理))已知命题:“”;命题:“函数单调递增”,则是的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不必要又不充分条件
题型二:必要不充分条件
4.(2022·贵州·模拟预测)已知曲线的方程,则“”是“曲线是圆”的( )
A.必要不充分条件B.充分不必要条件
C.充要条件D.既不充分也不必要条件
5.(2022·四川泸州·一模)已知直线m,n及平面,则“”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
6.(2022·全国·清华附中朝阳学校模拟预测)已知向量,,且,则“”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
题型三:充要条件
7.(2022·河北·模拟预测)已知中,,则的充要条件是( )
A.是等腰三角形B.
C.D.
8.(2022·黑龙江·哈尔滨市第一二二中学校三模(理))以下命题错误的序号为( )
①与是两条不同的直线,则“”是“”的充分不必要条件;
②若“”是真命题,则“”一定是假命题;
③荀子曰:不积跬步,无以至千里,不积小流,无以成江海.这说明“积跬步”是“至千里”的充分条件;
④“”是“为奇函数”的充要条件.
A.①③④B.①②C.③④D.①④
9.(2022·北京·高考真题)设是公差不为0的无穷等差数列,则“为递增数列”是“存在正整数,当时,”的( )
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分也不必要条件
题型四:简单的逻辑联结词
10.(2023·陕西西安·高三期末(理))已知命题过直线外一定点,且与该直线垂直的异面直线只有两条;命题,,则下列命题中为真命题的是( )
A.B.C.D.
11.(2022·河南·一模(理))已知,;,.若为真,则实数a的取值范围为( ).
A.B.C.D.
12.(2022·四川省绵阳南山中学模拟预测(理))已知命题,,命题函数在区间上是减函数,则,下列结构中正确的是( )
A.命题“”是真命题B.命题“”是真命题
C.命题“”是真命题D.命题“”是真命题
题型五:全称量词与存在量词
13.(2022·黑龙江·鸡东县第二中学二模)给出如下几个结论:
①命题“”的否定是“”;
②命题“”的否定是“”;
③对于;
④,使.
其中正确的是( )
A.③B.③④C.②③④D.①②③④
14.(2022·全国·高三专题)若“,使得”为假命题,则实数a的取值范围是( )
A.B.
C.D.
15.(2022·四川绵阳·一模(理))若命题“,”是真命题,则实数的取值范围是( )
A.B.C.D.
题型六:集合和逻辑用语的综合
16.(2022·四川省遂宁市教育局模拟预测(理))已知函数的值域为集合A,函数的定义域为集合B.
(1)当时,求;
(2)设命题,命题,若p是q的充分不必要条件,求实数的取值范围.
17.(2022·全国·高三专题练习)已知命题p:函数的值域为,命题q:,使得不等式.
(1)若p为真,求实数a的取值范围;
(2)若p∨q为真,p∧q为假,求实数a的取值范围.
18.(2022·河南·南阳中学模拟预测(理))已知,命题:函数仅有一个极值点;命题:函数在上单调递减.
(1)若为真命题,求的取值范围;
(2)若为真命题,为假命题,求的取值范围.
19.(2021·上海市行知中学高三开学考试)若数列满足(,且为实常数),,则称数列为数列.
(1)若数列的前三项依次为,,,且为数列,求实数的取值范围;
(2)已知是公比为的等比数列,且,记.若存在数列为数列,使得成立,求实数的取值范围;
(3)记无穷等差数列的首项为,公差为,证明:“”是“为数列”的充要条件.
【高考必刷】
一、单选题
20.(2022·天津·高考真题)“为整数”是“为整数”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
21.(2023·河南·洛宁县第一高级中学一模(理))已知命题,命题,则是q的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
22.(2022·四川省遂宁市教育局模拟预测(文))设m,n为实数,则“”是“”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
23.(2022·浙江绍兴·一模)已知数列为等差数列,前项和为,则“”是“数列为单增数列”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
24.(2022·福建·福州三中模拟预测)如果对于任意实数表示不超过的最大整数,那么“”是“成立”的( ).
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
25.(2023·广西·模拟预测(文))“”是“方程表示椭圆”的( )
A.必要不充分条件B.充分不必要条件
C.充要条件D.既不充分也不必要条件
26.(2022·新疆·兵团第一师高级中学高三阶段练习(理))下列命题正确的是( )
A.“”是“”的充分不必要条件
B.若给定命题,使得,则,均有
C.若为假命题,则p,q均为假命题
D.命题“若,则”的否命题为“若,则”
27.(2022·山东·汶上圣泽中学高三阶段练习)给出如下几个结论:
①命题“”的否定是“”;
②命题“”的否定是“”;
③对于;
④,使.
其中正确的是( )
A.③B.③④C.②③④D.①②③④
二、多选题
28.(2022·海南·模拟预测)已知命题:“”,"”,则下列正确的是( )
A.的否定是“”
B.的否定是“”
C.若为假命题,则的取值范围是
D.若为真命题,则的取值范围是
29.(2023·全国·高三专题)下列命题正确的是( )
A.正实数x,y满足,则的最小值为4
B.“”是“”成立的充分条件
C.若随机变量,且,则
D.命题,则p的否定:
30.(2022·全国·高三专题练习)已知公差为d的等差数列的前n项和为,则( )
A.是等差数列B.是关于n的二次函数
C.不可能是等差数列D.“”是“”的充要条件
31.(2022·河北·石家庄二中模拟预测)命题“”为真命题的一个充分不必要条件是( )
A.B.C.D.
32.(2023·全国·高三专题)在半径为10的圆上有三点M,N,C,其中M,N两点的坐标分别为、.现有两个命题如下:p:若∠MNC为60°,则三角形MNC的面积为;q:若,则四边形MCND的面积为.那么下列选项正确的是( )
A.命题p是真命题B.命题p是假命题
C.命题q是真命题D.命题q是假命题
三、填空题
33.(2022·四川省遂宁市教育局模拟预测(理))若命题:“,使”是假命题,则实数m的取值范围为____.
34.(2022·吉林省实验中学模拟预测(理))已知m,n是两条不重合的直线,是一个平面,,则“”是“”的__________条件.
35.(2022·全国·高三专题练习)设命题:;命题:关于的方程的两个实根均大于0.若命题“且”为真命题,求的取值范围为____.
36.(2021·安徽省定远中学模拟预测(文))设,,记命题:“”,命题:“”,若是的必要不充分条件,则的取值范围为______________.
四、解答题
37.(2022·黑龙江·齐齐哈尔三立高级中学有限公司高三期中)设函数的定义域为A,集合
(1)求集合A;
(2)若p:,q:,且p是q的必要不充分条件,求实数m的取值范围.
38.(2021·陕西·安康市教学研究室二模(理))已知为正数,不等式对恒成立;函数的最小值不小于2.
(1)若为真命题,求的取值范围;
(2)若为假命题,为真命题,求的取值范围.
若p⇒q,则p是q的充分条件,q是p的必要条件
p是q的充分不必要条件
p⇒q且q⇏p
p是q的必要不充分条件
p⇏q且q⇒p
p是q的充要条件
p⇔q
p是q的既不充分也不必要条件
p⇏q且q⇏p
名称
全称量词命题
存在量词命题
结构
将含有变量x的语句用p(x),q(x),r(x),…表示,变量x的取值范围用M表示
对M中任意一个x,p(x)成立
存在M中的元素x,p(x)成立
简记
∀x∈M,p(x)
∃x∈M,p(x)
否定
∃x∈M,p(x)
∀x∈M,p(x)
相关试卷
这是一份新高考数学一轮复习知识点总结与题型精练专题02 常用逻辑用语(含解析),共39页。
这是一份新高一预习:题型分类细讲精练11 函数性质综合大题(人教数学A版2019必修第一册),文件包含专题11函数性质综合大题人教A版2019必修第一册解析版docx、专题11函数性质综合大题人教A版2019必修第一册原卷版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
这是一份新高一预习:题型分类细讲精练06 函数:解析式归类(人教数学A版2019必修第一册),文件包含专题06函数解析式归类人教A版2019必修第一册解析版docx、专题06函数解析式归类人教A版2019必修第一册原卷版docx等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。








