重庆市九龙坡区、綦江区2022-2023学年七年级下学期期末质量监测数学试题

这是一份重庆市九龙坡区、綦江区2022-2023学年七年级下学期期末质量监测数学试题，共8页。试卷主要包含了选择题，填空题，解答题，选作题等内容，欢迎下载使用。

1．在下列各数中，是无理数的是（ ）
A．﹣2.010010001B．
C．D．π
2．若a＞b，则下列不等式一定不成立的是（ ）
A．2a﹣5＞2b﹣5B．﹣4a＞﹣4bC．a+1＞b+1D．
3．如图，直线a∥b，若∠1＝44°，则∠2的度数为（ ）
A．156°B．146°C．136°D．144°
4．下列调查中，最适合采用普查的是（ ）
A．升空前对火箭零部件的检测
B．调查某市中学生的视力状况
C．调查河水的污染情况
D．调查一批节能灯的使用寿命
5．如果点P（m+3，2m+4）在y轴上，那么点P的坐标是（ ）
A．（0，﹣2）B．（3，0）C．（1，0）D．（2，0）
6．估计的值在（ ）
A．5和6之间B．6和7之间C．7和8之间D．8和9之间
7．《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，木长多少尺？若设绳子长a尺，木长b尺，所列方程组正确的是（ ）
A．B．
C．D．
8．如图，AD∥BC，点P在射线BC上．AM，AN分别平分∠BAP，∠DAP，若∠DAN＝32°，且∠BAN＝∠BMA，则∠B的度数为（ ）
A．56°B．48°C．52°D．45°
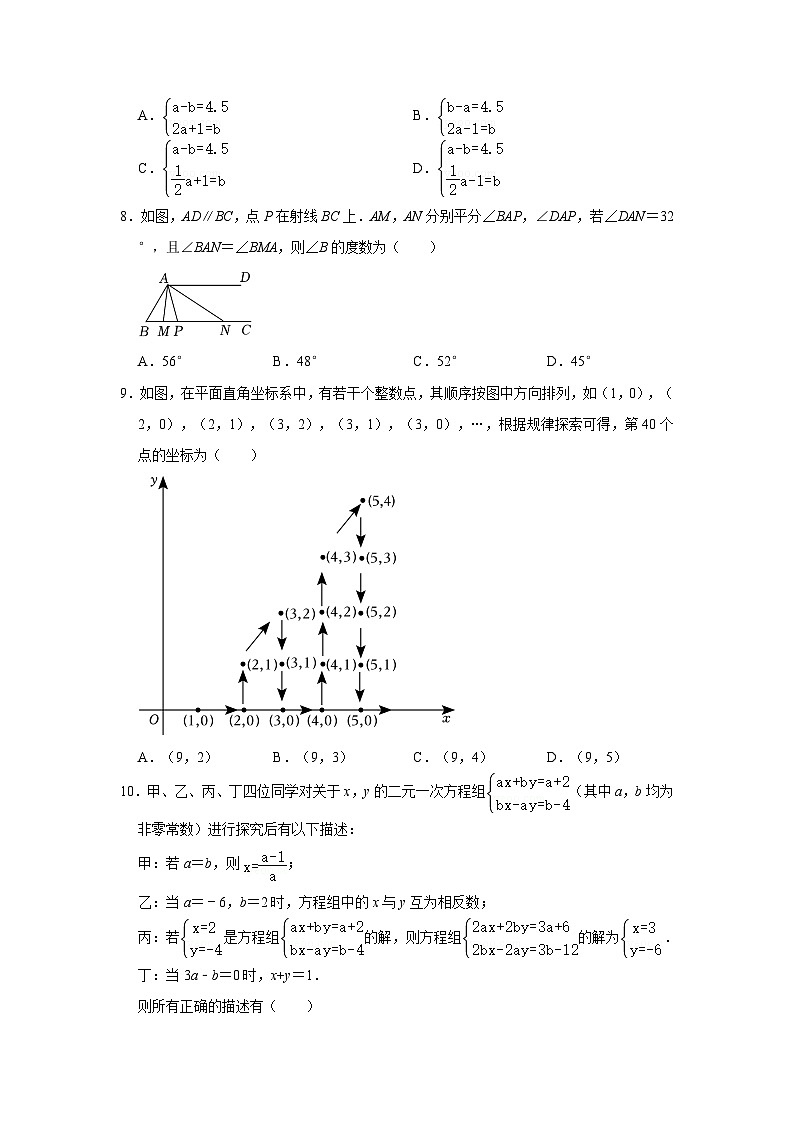
9．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0），…，根据规律探索可得，第40个点的坐标为（ ）
A．（9，2）B．（9，3）C．（9，4）D．（9，5）
10．甲、乙、丙、丁四位同学对关于x，y的二元一次方程组（其中a，b均为非零常数）进行探究后有以下描述：
甲：若a＝b，则；
乙：当a＝﹣6，b＝2时，方程组中的x与y互为相反数；
丙：若是方程组的解，则方程组的解为．
丁：当3a﹣b＝0时，x+y＝1．
则所有正确的描述有（ ）
A．4个B．3个C．2个D．1个
二、填空题：本大题8个小题，每小题4分，共32分，把答案填写在答题卡相应的位置上.
11．计算：＝ ．
12．在平面直角坐标系xOy中，点到x轴的距离是4，则A点的坐标是 ．
13．已知关于x的不等式x﹣a＞1的解集如图所示，则a的值等于
14．为了解我区九年级6000名学生中“1分钟跳绳”能获得满分的学生人数，区相关部门随机调查了其中的200名学生，结果有145名学生未获满分，那么估计我区九年级“1分钟跳绳”能获得满分的学生人数约为 名．
15．如图，设A，B的坐标分别为（﹣2，1），（0，﹣1）．若将线段AB平移至A1B1，A1B1的坐标分别为（a，3），（3，b），则的值为 ．
​
16．如图，长方形纸带ABCD中，AD∥CB，∠A＝∠B＝∠C＝∠D＝90°，将长方形ABCD沿EF折叠，C，D两点的对应点分别为G，H，若∠1＝2∠2，则∠AEF的度数为 .​
17．已知平面直角坐标系中的点在第四象限，且关于x的不等式组有且只有4个整数解，则符合条件的整数m的和为 ．
18．两个两位数p和q，将P的十位上的数字和个位上的数字分别放置于q的十位数字与个位之间和个位数字的右边，将q的十位上的数字和个位上的数字分别放置于p的十位数字与个位之间和个位数字的右边，就可以得到两个新四位数，把这两个新四位数的和与11的商记为F（p，q）．按此规则，计算F（13，26）＝ ；若a＝10+m，b＝10n+5，（0≤m≤9，1≤n≤9，m，n均为自然数），当150F（a，18）+F（b，26）＝32761时，则m+n的最大值为
三、解答题：本大题8个小题，第19题8分，其余每小题8分，共78分.解答时必须给出必要的演算过程或推理步骤，画出必要的图形(包括作辅助线），请将解答过程书写在答题卡中对应的位置上.
19．如图，平移三角形ABC，使点A平移到点A'．
（1）画出平移后的三角形A′B′C′（点B平移到B'，点C平移到C'，在图中标明相应字母，保留作图痕迹，不写作法）；
（2）结合（1）中的作图，猜想∠A′AB，∠ABC，∠BCC'的数量关系，并完成证明过程．
（2）猜想： ①；
证明：设 BB'与AC相交于点D，∵AA′∥BB′∥CC′，
∴∠A′AB＝ ②，∠BCC'＝∠DBC
∴∠ABC＝∠ABD+∠DBC＝ ③，
即， ④．
20．解方程组与不等式组：
（1）；
（2）解不等式组，并写出它的整数解．
21．为迎接区“双创”检查，某学校举行了“争双创、我做起”的宣传教育活动．为了解这次活动的效果，学校从全校3000名学生中随机抽取部分学生进行“24字”知识测试（测试满分100分，得分x均为不小于60的整数），并将测试成绩分为四个等级：基本合格（60≤x＜70），合格（70≤x＜80），良好（80≤x＜90），优秀（90≤x≤100），制作了如图统计图（部分信息未给出）．
由图中给出的信息解答下列问题：
（1）求测试成绩为合格的学生人数，并补全频数分布直方图．
（2）求扇形统计图中“良好”所对应的扇形圆心角的度数．
（3）如果全校学生都参加测试，请你根据抽样测试的结果，估计该校获得优秀的学生有多少人？
22．在学习了“数形结合”讨论问题后，某校数学兴趣小组开展“你命我解”互助学习活动．其中有一组的同学给出了这样一个问题：在平面直角坐标系xOy中，点中x，y的值若满足2x﹣y＝4，则称点Q为“直线点”，请你来解答这位同学提出的问题：
（1）判断点A（3，4）是否为“直线点”，并说明理由；
（2）若点M（a，2a﹣1）是“直线点”，请通过计算判断点M在第几象限？
23．如图，在平面直角坐标系xOy中，三角形ABC三个顶点的坐标分别是A（4，2），B（1，0），C（5，﹣3），三角形ABC中任意一点P（x0，y0），经平移后对应点为P′（x0﹣6，y0+2），将三角形ABC作同样的平移得到三角形A'B'C'，点A，B，C的对应点分别为A′，B′，C′．
（1）点A′的坐标为 ，点B′的坐标为 ；
（2）①画出三角形A′B′C′；
②写出三角形A′B′C′的面积；
（3）过点A′作A′D∥y轴，交B′C′于点D，则点D的坐标为 ．
24．某学校响应政策号召，开设了“1小时体育锻炼”活动，学生参加体育运用的热情高涨，参加足球和篮球人数大增，现有的足球和篮球不够用了．为解决这一问题，学校准备从体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同）．经调查：若购买30个足球和20个篮球共需4800元，购买10个足球和30个篮球共需4400元．
（1）求购买一个足球、一个篮球各需多少元；
（2）学校准备购买足球和篮球共50个，且篮球数量不少于足球数量的预算经费不超过4600元，请设计出最省钱的购买方案，并说明理由．
25．如图，△ABC中，点A、点C在x轴上，点B在第一象限，直线AB上任一点的坐标（x，y），都使方程x﹣y＝﹣2成立，直线BC上任一点的坐标（x，y）都使方程2x+y＝8
成立．
（1）求B点的坐标时，小明是这样想的：先设B点坐标为（m，n），因为B点在直线AB上，所以（m，n）使方程x﹣y＝﹣2成立；又因为B点在直线BC上，所以（m，n）使方程2x+y＝8成立，从而m，n满足．据此可求出B点坐标为 ，再求出A点坐标为 ；C点坐标为 ．
（2）点D是线段BC上一点，若（O为原点），求D点坐标；
（3）点E（a，﹣3）是坐标平面内的动点，若满足，求a的值．
26．如图，点E、F分别是直线AB、CD上的一点，连接EF，点P是线段EF上一点，FM平分∠PFC，交直线AB于点M，射线MP交直线CD于点N．设∠EPN＝x°，∠PEB＝y°，∠PND＝z°，其中x、y、z满足
（1）求x，y，z的值；
（2）求证：AB∥CD；
（3）过点P作直线QR分别交直线AB于点Q，交直线CD于点R，且Q不与M重合，R不与N重合．作∠MQR的角平分线交线段MF于点S，直接写出∠FSQ与∠FPQ的数量关系．
四、选作题：本大题1个小题，共20分，不计入总分.解答时必须给出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上.
27．我们常用符号[x]表示小于或者等于x的最大整数．例如[0]＝0，[2.3]＝2，[﹣2.5]＝﹣3[π]＝3．由此可以知道，当x为整数时，[x]＝x．
请根据以上信息，解决下列问题：
（1）[1.2]＝ [﹣3.8]＝ [2π]＝ ．
（2）计算并找规律
[1]+[﹣1]＝ [200]+[﹣200]＝
[1.5]+[﹣1.5]＝ [3.14]+[﹣3.14]＝
根据以上计算，可归纳出：
①当x为整数时，[x]+[﹣x]＝ ．
②当x不为整数时，[x]+[﹣x]＝ ．
（3）计算：
（4）解关于x的方程
x+[2x]+[4x]+[6x]+…+[18x]+[20x]＝1332