2024年广东省广州市天河区九年级中考二模数学试题(无答案)

这是一份2024年广东省广州市天河区九年级中考二模数学试题(无答案)，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本题有10个小题，每小题3分，满分30分，每小题给出的四个选项中，只有一个是正确的．）
1．欢欢放学回家看到弟弟用几个小正方体的积木搭建出如图的几何体，她用手机拍照得到这个几何体的三视图，其中左视图是（ ）．
A．B．C．D．
2．民间剪纸是劳动人民为了满足精神生活需要而创造的，具有鲜明的艺术特色和生活情趣．下列剪纸图形是中心对称图形的是（ ）．
A．B．C．D．
3．正比例函数的图象经过点，则此图象一定经过点（ ）．
A．B．C．D．
4．下列运算不正确的是（ ）．
A．B．C．D．
5．代数式有意义时，则x应满足的条件是（ ）．
A．B．C．D．
6．彤彤在班上做节水意识调查，收集了班上7位同学家里上个月的用水量（单位：）如下：7，5，13，6，9，11，5．这组数据的中位数和平均数分别是（ ）．
A．7，6B．6，7C．6，8D．7，8
7．有理数a，b在数轴上的对应点的位置如图所示，把a，，b按照从小到大的顺序排列，正确的是（ ）．
A．B．C．D．
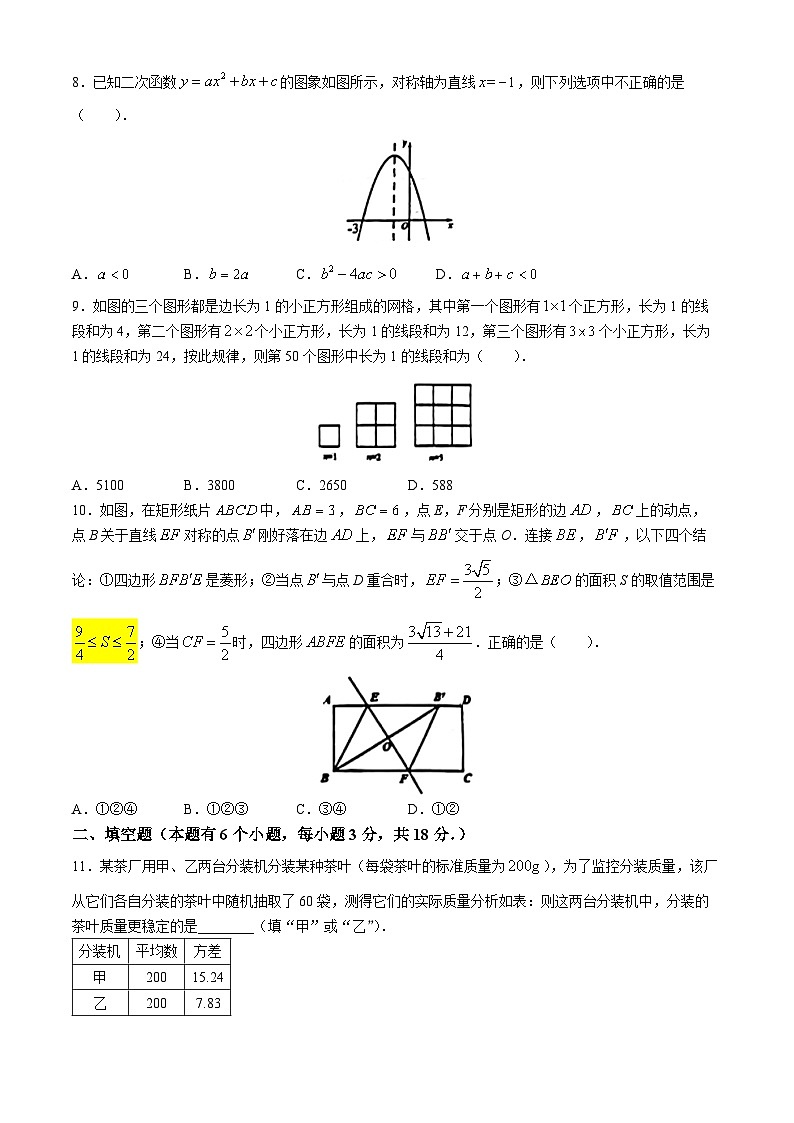
8．已知二次函数的图象如图所示，对称轴为直线，则下列选项中不正确的是（ ）．
A．B．C．D．
9．如图的三个图形都是边长为1的小正方形组成的网格，其中第一个图形有个正方形，长为1的线段和为4，第二个图形有个小正方形，长为1的线段和为12，第三个图形有个小正方形，长为1的线段和为24，按此规律，则第50个图形中长为1的线段和为（ ）．
A．5100B．3800C．2650D．588
10．如图，在矩形纸片中，，，点E，F分别是矩形的边，上的动点，点B关于直线对称的点刚好落在边上，与交于点O．连接，，以下四个结论：①四边形是菱形；②当点与点D重合时，；③的面积S的取值范围是；④当时，四边形的面积为．正确的是（ ）．
A．①②④B．①②③C．③④D．①②
二、填空题（本题有6个小题，每小题3分，共18分．）
11．某茶厂用甲、乙两台分装机分装某种茶叶（每袋茶叶的标准质量为），为了监控分装质量，该厂从它们各自分装的茶叶中随机抽取了60袋，测得它们的实际质量分析如表：则这两台分装机中，分装的茶叶质量更稳定的是________（填“甲”或“乙”）．
12．因式分解：________．
13．某班去研学，有两种套票可供选择，已知甲种套票每张80元，乙种套票每张70元，如果每人只购买其中一种，40名学生恰好用去2900元，那么该班购买甲种套票的张数是________．
14．的对角线，相交于点O，是等边三角形，，则的面积等于________．
15．如图，是的直径，是弦，且，，则与的长度的比值为________．
16．中，，，点D是边的中点，把点D绕点B逆时针旋转得到点E，连接，则线段的最小值是________．
三、解答题（本大题有9小题，共72分，解答要求写出文字说明，证明过程或计算步骤．）
17．（本题满分4分）
解分式方程．
18．（本题满分4分）
古人诗云：“草长莺飞二月天，拂堤杨柳醉春烟。儿童散学归来早，忙趁东风放纸鸢。”纸鸢，又称风筝，其制作技艺是我国民间的传统工艺，某班数学兴趣小组根据风筝的形状画出图形（如图所示），已知，，求证：．
19．（本题满分6分）
某校七年级开展数学文化节活动，推荐给同学们三本数学课外读物，分别是《生活中的数学》《数学家的故事》《奇妙数世界》，小聪和小华将这三本书的书名写在形状大小、颜色完全相同的三张卡纸上，并把卡纸反放在桌面，先由小聪随机抽一张卡纸，记录书名后放回，再由小华抽一张卡纸，记录书名．
（1）填空：小聪抽到《数学大爆炸》是________事件；（填“必然”，“不可能”，“随机”）
（2）请用树状图或者列表法，求小聪和小华两个人中至少一个人抽中《奇妙数世界》的概率．
20．（本题满分6分）
一艘载满货物的轮船到达南沙港码头后开始卸货。平均卸货速度y（单位：吨/天）与卸货天数t是反比例函数关系，它的图象如图所示．
（1）求y与t之间的函数解析式；
（2）南沙港码头收到气象部门的紧急通知，在某海域形成新的台风，预计7天后影响码头卸货，因此要求船上的货物不超过5天卸载完毕，那么平均每天至少要卸载多少吨？
21．（本题满分8分）
已知．
（1）化简T；
（2）若a，b互为相反数，求T的值．
22．（本题满分10分）
如图，中，E是边的中点，，垂足是D．
（1）作的高（尺规作图，保留作图痕迹）；
（2）连接，若，求的值．
23．（本题满分10分）
小亮同学将一辆自行车水平放在地面上．如示意图，车把头下方A处与坐垫下方B处的连线平行于地面水平线，C处为齿盘的中轴，测得，，
（1）求的长度（结果保留整数）；
（2）若点C到地面的距离为，坐垫中轴E与点B的距离为，根据小亮同学身高比例，坐垫E到地面的距离为至之间时，骑乘该自行车最舒适，请你通过计算判断出小亮同学骑乘该自行车是否能达到最佳舒适度．
（参考数据：，，，）
24．（本题满分12分）
如图1，正方形中，点E是边上任意一点（不与点B重合），以为边在它的外侧作正方形，点M和点P分别是这两个正方形的对称中心，连接．
（1）填空：当时，线段长的最大值是________；
（2）在正方形的边上，是否存在一点Q，使得为等腰直角三角形？若存在，通过证明确定所有满足条件的点Q的具体位置；若不存在，请说明理由；
（3）如图2．连接并延长，与交于点O．求的度数，并求出与的数量关系．
25．（本题满分12分）
在平面直角坐标系中，将过点的抛物线（b为常数）向右平移m个单位（），再向上平移n个单位（）得到新的抛物线，其顶点为E．
（1）求点E的坐标；（用含m，n的式子表示）
（2）若抛物线与坐标轴有且只有两个公共点，求满足条件的点E的纵坐标；
（3）当时，抛物线与x轴交于A、B两点，与y轴交于点D，且当时，对抛物线上的任意一点P，在抛物线上总存在一点Q，使得点P，Q的纵坐标相等，探究下列问题：
①求m的取位范围；
②若存在一点F，满足，求点F的纵坐标的取值范围．分装机
平均数
方差
甲
200
15.24
乙
200
7.83