2024年广东省揭阳市普宁市中考数学二模试卷（含详细答案解析）

这是一份2024年广东省揭阳市普宁市中考数学二模试卷（含详细答案解析），共22页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。
1.凝固点是晶体物质凝固时的温度，则在标准大气压下，下列物质中凝固点最低的是( )
A. 钨B. 水银C. 煤油D. 水
2.数学中处处存在着美，从三国时期的赵爽弦图，到19世纪的莱洛三角形，再到近代的科克曲线和谢尔宾斯基三角形，这种特殊的数学之美，令人沉述.下列图形中，既是中心对称图形，又是轴对称图形的是( )
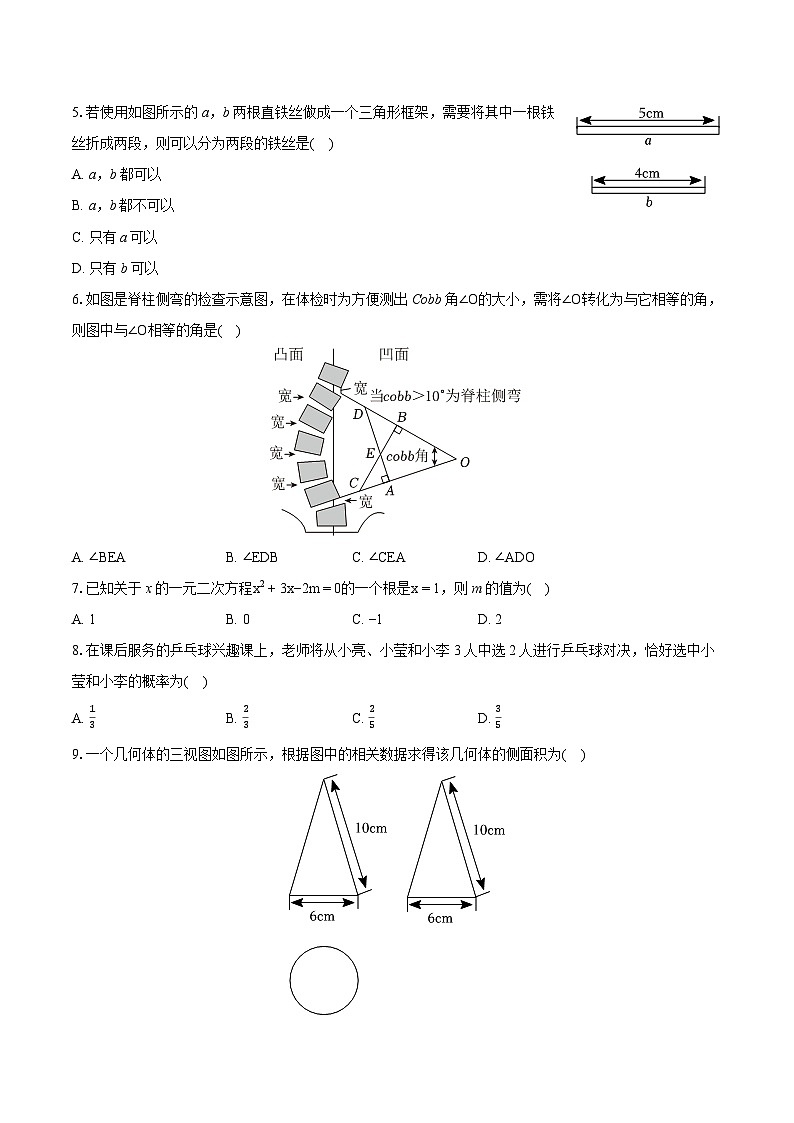
A. 赵爽弦图B. 莱洛三角形
C. 科克曲线D. 谢尔宾斯基三角形
3.如图是一款折叠LED护眼灯示意图，AB是底座，CD、DE分别是长臂和短臂，点C在AB上，若DE//AB，∠DCA=70∘，则长臂和短臂的夹角∠CDE=( )
A. 120∘
B. 100∘
C. 70∘
D. 110∘
4.下列计算正确的是( )
A. a3⋅a4=a12B. (a3)4=a7C. a3+a2=a5D. a4+a4=2a4
5.若使用如图所示的a，b两根直铁丝做成一个三角形框架，需要将其中一根铁丝折成两段，则可以分为两段的铁丝是( )
A. a，b都可以
B. a，b都不可以
C. 只有a可以
D. 只有b可以
6.如图是脊柱侧弯的检查示意图，在体检时为方便测出Cbb角∠O的大小，需将∠O转化为与它相等的角，则图中与∠O相等的角是( )
A. ∠BEAB. ∠EDBC. ∠CEAD. ∠ADO
7.已知关于x的一元二次方程x2+3x−2m=0的一个根是x=1，则m的值为( )
A. 1B. 0C. −1D. 2
8.在课后服务的乒乓球兴趣课上，老师将从小亮、小莹和小李3人中选2人进行乒乓球对决，恰好选中小莹和小李的概率为( )
A. 13B. 23C. 25D. 35
9.一个几何体的三视图如图所示，根据图中的相关数据求得该几何体的侧面积为( )
A. 60πcm2B. 40πcm2C. 30πcm2D. 24πcm2
10.如图，已知A，B是反比例函数y=kx(k>0,x>0)图象上的两点，BC//x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C(图中“→”所示路线)匀速运动，终点为C，过P作PM⊥x轴，垂足为M.设三角形OMP的面积为S，P点运动时间为t，则S关于t的函数图象大致为( )
A. B. C. D.
二、填空题：本题共6小题，每小题3分，共18分。
11.计算a2a+2−4a+2的结果为______.
12.科学家们测得光在水中的速度约为225000000米/秒，数字225000000用科学记数法表示为______.
13.如图，在杭州举行的第19届亚运会的奖牌取名“湖山”，以良渚文化中的礼器玉琮为表征，其外轮廓为八边形.这个八边形的内角和是______度.
14.如图所示的衣架可以近似看成一个等腰三角形ABC，其中AB=AC，∠ABC=27∘，BC=44cm，则高AD约为______cm.(结果精确到0.1cm，参考数据：sin27∘≈0.45，cs27∘≈0.89，tan27∘≈0.51)
15.一商场先用3200元购进一批防紫外线太阳伞，很快就销售一空.商场又用8000元购进了第二批这种太阳伞，所购数量是第一批的2倍，但每把太阳伞贵了4元.则第一次购进这种太阳伞______把.
16.如图，正方形ABCD的边长为4，点E，F分别在边BC，CD上，AE平分∠BAC，连接BF，分别交AE，AC于点G，H，且AE=BF.有下列四个结论：①AE垂直平分BH；②若点P是边AB上的一个动点，则PH+PC的最小值为4 3；③GH2=AG⋅EG；④S△ABH=6 2.其中正确的有______.
三、计算题：本大题共1小题，共4分。
17.计算：(x−y)2−x(x−2y)
四、解答题：本题共8小题，共68分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题4分)
计算：−12024+(−12)0− 3× 6.
19.(本小题6分)
解不等式组x<5x+234x−2<4+x，并把解集表示在数轴上.
20.(本小题6分)
如图，在平行四边形ABCD中，E是AD边上一点.
(1)过点E作AB的平行线EF，交BC于点F(尺规作图，保留作图痕迹，不写作法).
(2)在(1)的条件下，求证：△BAE≌△EFB.
21.(本小题8分)
蓬勃发展的快递业，为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.草莓种植户小丽经过初步了解，打算从甲、乙两家快递公司中选择一家合作，为此小丽收集了10家草莓种植户对两家公司的相关评价，并整理、描述、分析，下面给出了部分信息：a.配送速度得分(满分10分)：
甲：6 7 7 8 8 8 8 9 9 10
乙：7 7 8 8 8 9 9 9 10 10
b.服务质量得分统计图(满分10分)：
c.配送速度和服务质量得分统计表：
根据以上信息，回答下列问题：
(1)求出表中m，n的值；
(2)在甲乙两家快递公司中，如果某公司服务质量得分的10个数据的波动越小，则认为种植户对该公司的评价越一致.据此推断：甲、乙两家公司中，种植户对______的服务质量的评价更一致(填“甲”或“乙”)；
(3)根据以上数据，小丽应该选择哪一家快递公司？请说明理由.(写出一条理由即可)
22.(本小题10分)
我市某校为了落实“阳光体育活动”，在八年级开展了篮球赛.比赛规则是：八年级10个班级每个班级派出一支队伍参赛，赛制采用的是单循环积分赛(每个班级都与其他9个班级进行一场比赛)，胜一场记2分，负一场记1分，然后按照积分高低进行排名.赛程过半，小明所在的班级已经进行了5场比赛，积9分.
(1)求小明所在班级胜、负的场次各是多少；
(2)根据分析，总积分超过15分才能确保进入前两名，小明的班级若想进入前两名在剩下的比赛中至少还要取得几场胜利？
23.(本小题10分)
综合与实践
不借助科学计算器，如何求tan22.5∘的值？小明进行了如下的实践操作：
如图，已知正方形纸片ABCD.
第一步：将正方形纸片ABCD沿AC折叠，展开后得到折痕AC.
第二步：将AB折叠到AF，使点B的对应点F恰好落在AC上，展开后得到折痕AE，点E在线段BC上，连接EF.
问题解决：
(1)求证：∠BAE=22.5∘；
(2)请利用小明的实践操作过程，求tan22.5∘的值.
24.(本小题12分)
如图，在▱ABCD中，连接BD，以DF为直径的半圆O，从DF与AD共线开始绕点D逆时针旋转，直线DF与DC第一次重合时，停止运动，点K是半圆O的中点，连接DK，当DF，DK与线段AB有交点时，设交点分别为点P和点Q，已知AB=DF=8，∠BAD=45∘，AD=BD.
(1)求∠FDK的度数；
(2)当点Q在AB上时，设AQ=x，BP=y，请求出y与x的关系式；
(3)当DF与DB重合时，求半圆O与DC所围成的弓形的面积.
25.(本小题12分)
综合与探究：
如图1，抛物线y=ax2+bx+54与x轴相交于A(12,0)，B(52,0)两点，与y轴交于点C，连接BC，抛物线顶点为点M.
(1)求抛物线解析式及点M的坐标；
(2)平移直线BC得直线y=mx+n.
①如图2，若直线y=mx+n过点M，交x轴于点D，在x轴上取点E(76,0)，连接EM，求∠DME的度数.
②把抛物线y=ax2+bx+54在x轴下方图象沿x轴翻折得到新图象(如图3中的“W”形曲线).当直线y=mx+n与新图象有两个公共点时，请直接写出n的取值范围.
答案和解析
1.【答案】B
【解析】解：∵−38.87<−30<0<3412，
∴物质中凝固点最低的是水银．
故选：B.
先确定正数和负数，然后确定最小的数即可解答．
本题考查了正数和负数以及有理数比较大小，解题的关键是根据有理数大小比较的法则正确比较大小．
2.【答案】C
【解析】解：A.该图形是中心对称图形，不是轴对称图形，故此选项不符合题意；
B.该图形是轴对称图形，不是中心对称图形，故此选项不符合题意；
C.该图形既是轴对称图形，又是中心对称图形，故此选项符合题意；
D.该图形是轴对称图形，不是中心对称图形，故此选项不符合题意．
故选：C.
中心对称图形的定义：把一个图形绕某一点旋转180∘，如果旋转后的图形能与原来的图形重合，那么这个图形就叫做中心对称图形；轴对称图形的定义：如果一个图形沿着一条直线对折后两部分完全重台，这样的图形叫做轴对称图形．根据定义依次对各个选项进行判断即可．
本题考查了中心对称图形与轴对称图形的概念．正确掌握中心对称图形与轴对称图形定义是解题关键．
3.【答案】D
【解析】解：∵DE//AB，
∴∠DCA+∠CDE=180∘，
∵∠DCA=70∘，
∴∠CDE=180∘−∠DCA=110∘，
故选：D.
利用两直线平行，同旁内角互补进行计算，即可解答．
本题考查了平行线的性质，熟练掌握平行线的性质是解题的关键．
4.【答案】D
【解析】解：a3⋅a4=a7，则A不符合题意；
(a3)4=a12，则B不符合题意；
a3，a2不是同类项，无法合并，则C不符合题意；
a4+a4=2a4，则D符合题意；
故选：D.
利用同底数幂乘法法则，幂的乘方法则及合并同类项法则将各式计算后进行判断即可．
本题考查同底数幂乘法，幂的乘方及合并同类项，熟练掌握相关运算法则是解题的关键．
5.【答案】C
【解析】解：三角形两边之和大于第三边，两根长度分别为5cm和4cm的细木条做一个三角形的框架，可以把5cm的细木条分为两截．
理由：5>4，满足两边之和大于第三边．
故选：C.
三角形两边之和大于第三边．依此即可求解．
本题考查了三角形的三边关系，关键掌握三角形两边之和大于第三边，两边之差小于第三边．
6.【答案】C
【解析】解：由示意图可知，△DOA和△DBE都是直角三角形，
∴∠O+∠ADO=90∘，∠DEB+∠ADO=90∘，
∴∠DEB=∠O，
∴∠DEB=∠CEA，
∴∠CEA=∠O.
故选：C.
根据直角三角形的性质可知，∠O与∠ADO互余，∠DEB与∠ADO互余，根据同角的余角相等可得∠DEB=∠O，再根据对顶角相等即可得出结论．
本题考查了多边形的内角和外角，掌握直角三角形的两个锐角互余是解题的关键．
7.【答案】D
【解析】解：由题意得：
把x=1代入方程x2+3x−2m=0中得：
12+3×1−2m=0，
1+3−2m=0，
−2m=−1−3，
−2m=−4，
m=2，
故选：D.
把x=1代入方程x2+3x−2m=0中得：12+3×1−2m=0，然后进行计算即可解答．
本题考查了一元二次方程的解，熟练掌握一元二次方程的解的意义是解题的关键．
8.【答案】A
【解析】解：树状图如下所示，
由上可得，一共有6种等可能性，其中恰好选中小莹和小李的可能性有2种，
∴恰好选中小莹和小李的概率为26=13，
故选：A.
根据题意，可以画出相应的树状图，然后即可求出恰好选中小莹和小李的概率．
本题考查列表法与树状图法，解答本题的关键是明确题意，画出相应的树状图，求出相应的概率．
9.【答案】C
【解析】解：由三视图得这个几何体为圆锥，圆锥的母线长为10cm，底面圆的直径为6cm，
所以这个几何体的侧面积=12×π×10×6=30π(cm2).
故选：C.
先判断这个几何体为圆锥，同时得到圆锥的母线长为10cm，底面圆的直径为6cm，然后利用扇形的面积公式计算这个圆锥的侧面积．
本题考查了由三视图判断几何体，圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了三视图．
10.【答案】A
【解析】解：设∠AOM=α，点P运动的速度为a，
当点P从点O运动到点A的过程中，S=(at⋅csα)⋅(at⋅sinα)2=12a2⋅csα⋅sinα⋅t2，
由于α及a均为常量，从而可知图象本段应为抛物线，且S随着t的增大而增大；
当点P从A运动到B时，由反比例函数性质可知△OPM的面积为12k，保持不变，
故本段图象应为与横轴平行的线段；
当点P从B运动到C过程中，OM的长在减少，△OPM的高与在B点时相同，
故本段图象应该为一段下降的线段；
故选：A.
结合点P的运动，将点P的运动路线分成O→A、A→B、B→C三段位置来进行分析三角形OMP面积的计算方式，通过图形的特点分析出面积变化的趋势，从而得到答案．
本题考查了反比例函数图象性质、锐角三角函数性质，解题的关键是明确点P在O→A、A→B、B→C三段位置时三角形OMP的面积计算方式．
11.【答案】a−2
【解析】解：a2a+2−4a+2
=a2−4a+2
=(a+2)(a−2)a+2
=a−2，
故答案为：a−2.
运用同分母分式相加减的方法进行计算、约分化简．
此题考查了分式加减的运算能力，关键是能准确理解并运用该知识进行计算和化简．
12.【答案】2.25×108
【解析】解：225000000=2.25×108，
故答案为：2.25×108.
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．
13.【答案】1080
【解析】解：这个八边形的内角和是(8−2)×180∘=1080∘.
故答案为：1080.
利用n边形内角和定理：n边形的内角和等于(n−2)⋅180∘解答即可．
本题主要考查了多边形的内角和定理，熟练掌握多边形的内角和定理是解题的关键．
14.【答案】11.2
【解析】解：∵AB=AC，AD⊥BC，
∴BD=12BC=22(cm)，
在Rt△ABD中，∠ABC=27∘，
∴AD=BD⋅tan27∘≈22×0.51≈11.2(cm)，
∴高AD约为11.2cm，
故答案为：11.2.
先利用等腰三角形的三线合一性质可得BD=22cm，然后在Rt△ABD中，利用锐角三角函数的定义进行计算，即可解答．
本题考查了解直角三角形的应用，等腰三角形的性质，熟练掌握锐角三角函数的定义是解题的关键．
15.【答案】200
【解析】解：设商场第一批购进x把这种太阳伞，则第二批购进2x把这种太阳伞，
根据题意得：80002x−3200x=4，
解得：x=200，
经检验，x=200是所列方程的解，且符合题意，
故答案为：200.
设商场第一批购进x把这种太阳伞，则第二批购进2x把这种太阳伞，利用单价=总价÷数量，结合第二批的购进单价比第一批贵4元，可得出关于x的分式方程，解之经检验后可得出x的值，再将其代入x+2x中，即可求出结论．
本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．
16.【答案】①②③
【解析】解：①∵四边形ABCD是正方形，
∴AB=BC，∠ABC=∠BCF=90∘，
在Rt△ABE和Rt△BCF中
AE=BFAB=BC，
∴Rt△ABE≌Rt△BCF(HL)，
∴∠BAE=∠CBF，
∵∠ABF+∠CBF=90∘，
∴∠ABF+∠BAE=90∘，
∴AG⊥BH，
∵AE平分∠BAC，
∴∠BAE=∠CAE，
∵AG⊥BH，
∴∠AGB=∠AGH=90∘，
在Rt△ABG和Rt△AHG中，
∠BAE=∠CAEAG=AG∠AGB=∠AGH，
∴Rt△ABG≌Rt△AHG(ASA)，
∴BG=HG，
∴AE垂直平分BH，
故①正确；
②延长CB至M，使BM=BC=4，过点H作HN⊥BC于点N，如图，
则点M与点C关于AB对称，连接MH交AB于点P，
在Rt△PMB和Rt△PCB中，
BM=BC∠PBM=∠PBCPB=PB，
∴Rt△PMB≌Rt△PCB(SAS)，
∴PM=PC，
∵四边形ABCD是正方形，AB=BC=4，
∴AC=4 2，
∵Rt△ABG≌Rt△AHG，
∴AB=AH=4，
∴HC=4 2−4，
在Rt△HCN中，∠HCN=45∘，
∴HN=CN，
∴HN2+CN2=HC2，
∴HN=CN=4−2 2，
∴MN=BM+BN=4+2 2，
∴在Rt△HNM中
MH= MN2+HN2=4 3，
∴PH+PC的最小值是4 3，
故②正确；
③连接EH，如图，
∵Rt△ABG≌Rt△AHG，
∴AB=AH，
在△ABE和△AHE中，
AB=AH∠BAE=∠HAEAE=AE，
∴△ABE≌△AHE(SAS)，
∴∠ABE=∠AHE=90∘，
∴AH⊥EH，
∴四边形ABEH在以AE为直径的圆上，
∵∠BAG=∠EHG∠AGB=∠HGE，
∴△ABG∽△HEG，
∴BGEG=AGHG，
∴HG⋅BG=AG⋅EG，
∵BG=HG，
∴GH2=AG⋅EG；
故③正确；
④由②知，BN=2 2，
∴S△ABH=12×AB×BN
=12×4×2 2
=4 2，
故④错误．
故答案为：①②③．
①根据四边形ABCD是正方形，可知AB=BC，∠ABC=∠BCF=90∘，证明Rt△ABE≌Rt△BCF(HL)，有∠BAE=∠CBF，进而可得∠AGB=90∘，AG⊥BH，再利用AE平分∠BAC，∠BAE=∠CAE，再证明Rt△ABG≌Rt△AHG(ASA)，得到BG=HG，从而可知AE垂直平分BH，从而可知①正确；
②延长CB至M，使BM=BC=4，过点H作HN⊥BC于点N，则点M与点C关于AB对称，连接MH交AB于点P，此时确定点P使PH+PC取最小值，先证明Rt△PMB≌Rt△PCB(SAS)，得到PM=PC，求出AC的值，利用Rt△ABG≌Rt△AHG得到AB=AH=4，再求出HC的值，利用勾股定理求得HN的值，在Rt△HNM中利用勾股定理即可求得MH的值，从而可知②正确；
③连接EH，利用Rt△ABG面Rt△AHG得到AB=AH，先证△ABE≌△AHE(SAS)，有∠ABE=∠AHE=90∘，AH⊥EH，从而确定四边形ABEH在以AE为直径的圆上，再证△ABG∽△HEG，得到BGEG=AGHG，有BG=HG，得到GH2=AG⋅EG，从而可知③正确；
④利用S△ABH=12×AB×BN=4 2，从而可知④错误．
本题考查了正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理和四点共圆等知识，利用好全等三角形和相似三角形等知识是解题的关键．
17.【答案】解：(x−y)2−x(x−2y)
=x2−2xy+y2−x2+2xy
=y2.
【解析】本题考查了完全平方公式，单项式与多项式相乘的法则．熟练掌握运算法则是解题的关键，计算时要注意符号的处理．
根据完全平方公式，单项式与多项式相乘的法则计算即可．
18.【答案】解：原式=−1+1− 18
=1−1−3 2
=−3 2.
【解析】先根据乘方的意义和零指数幂的性质计算乘方，再根据二次根式的乘法法则计算乘法，最后算加减即可．
本题主要考查了二次根式的混合运算，解题关键是熟练掌握二次根式的乘法法则、乘方的意义和零指数幂的性质．
19.【答案】解：{x<5x+23①4x−2<4+x②，
解不等式①，得：x>−1，
解不等式②，得：x<2，
∴原不等式组的解集为−1其解集在数轴上表示如下：
.
【解析】先解出每个不等式的解集，即可得到不等式组的解集，然后在数轴上表示出其解集即可．
本题考查解一元一次不等式组、在数轴上表示不等式的解集，解答本题的关键是明确解一元一次不等式的方法．
20.【答案】(1)解：(作法不唯一)如图，EF即为所求；
(2)证明：∵四边形ABCD是平行四边形，
∴AD//BC，
∴∠AEB=∠FBE.
又∵EF//AB，
∴∠ABE=∠FEB，
又∵AE=BF，
∴△BAE≌△EFB(ASA).
【解析】(1)在BC上截取BF=AE，连接EF，则EF即为所求；
(2)根据平行四边形的性质以及平行线的性质推出AEB=∠FBE，∠ABE=∠FEB，再结合AE=BF即可得出结论．
本题考查了作图-复杂作图，平行四边形的性质，全等三角形的判定与性质，熟记各性质定理是解题的关键．
21.【答案】甲
【解析】解：(1)甲的平均数m=110×(6+7+7+8+8+8+8+9+9+10)=8(分)，
乙服务质量得分为4、5、5、6、6、7、8、9、10、10，
其中位数n=6+72=6.5(分)；
(2)由折线统计图知，甲公司服务质量得分的波动幅度明显小于乙公司，
所以甲、乙两家公司中，种植户对甲的服务质量的评价更一致，
故答案为：甲；
(3)选择乙公司，
从配送速度角度，甲公司的配送速度的平均数小于乙公司，
所以选择乙公司(答案不唯一).
(1)根据平均数和中位数的定义求解即可；
(2)根据方差的意义求解即可；
(3)根据平均数、中位数及方差的意义，分别从配送速度和服务质量角度分析求解即可，答案不唯一．
本题考查了方差，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立，也考查了平均数、中位数．关键是能根据平均数、中位数、方差的意义对本题进行分析．
22.【答案】解：(1)设小明所在班级胜了x场，负了y场，
依题意得x+y=52x+y=9，
解得x=4y=1，
∴小明所在班级胜了4场，负了1场；
(2)设小明的班级在剩下的比赛中还要胜m场，
依题意，得2m+9−5−m+9>15，
解得m>2，
∵m为正整数，
∴m≥3，
∴小明的班级在剩下的比赛中至少还要胜3场．
【解析】(1)设小明所在班级胜了x场，负了y场，根据小明所在的班级已经进行了5场比赛，积9分，即可得出关于x，y的二元一次方程组，解之即可得出结论；
(2)设小明的班级在剩下的比赛中还要胜m场，根据总积分超过15分才能确保进入前两名，即可得出关于m的一元一次不等式，解之取其中的最小整数值即可得出结论．
本题考查了二元一次方程组，一元一次不等式的应用，解题的关键是找准等量关系，正确列出二元一次方程组．
23.【答案】(1)证明：由正方形纸片ABCD沿AC折叠，
得AF=AB，EF=EB，∠AFE=∠B=90∘，∠BAC=45∘，
得∠BAE=12∠BAC=22.5∘；
(2)设EF=EB=1，
得FC=FE=1，EC= 12+12= 2，
得AF=AB=BC= 2+1，
得tan22.5∘=tan∠BAE=1 2+1= 2−1.
【解析】(1)由正方形纸片ABCD沿AC折叠，得AF=AB，EF=EB，∠AFE=∠B=90∘，∠BAC=45∘，即可得∠BAE=12∠BAC=22.5∘；
(2)设EF=EB=1，得FC=FE=1，EC= 12+12= 2，得AF=AB=BC= 2+1，即可得tan22.5∘=tan∠BAE=1 2+1= 2−1.
本题主要考查了折叠，解题关键是正确计算．
24.【答案】解：(1)连接FK，如图1所示：
∵点K为半圆O的中点，
∴DK=FK，
∴DK=FK，
∵DF为直径，
∴∠DKF=90∘，
在Rt△DFK中，∠FDK=∠DFK=45∘；
(2)如图2所示：
∵∠BAD=45∘，AD=BD，
∴∠DAB=∠PDK=45∘=∠ABD，
∴在等腰Rt△ABD中，AB=8，则由勾股定理可得AD=DB=4 2，
∵∠DPB=∠DAB+∠ADP=45∘+∠ADP，∠ADQ=∠PDQ+∠ADP=45∘+∠ADP，
∴∠DPB=∠ADQ，
∴△ADQ∽△BPD，
∴ADBP=AQBD，
∴BP=AD⋅BDAQ=(4 2)2x=32x，
y与x的关系式为y=32x；
(3)当DF与DB重合时，
∵∠BDC=∠ODK=45∘，
∴点K在DC上，连接OK，如图3所示：
∵点K是半圆O的中点，
∴∠DOK=90∘.
∵DO=12DF=4，
∴S扇形DOK=90360×π×42=4π，S△DOK=12DO⋅OK=12×42=8，
∴半圆O与DC所围成的封闭图形的面积为S扇形DOK−S△DOK=4π−8.
【解析】(1)连接FK，如图所示，由弧相等得到弦相等，再由直径所对的圆周角是直角，利用等腰直角三角形性质即可得到答案；
(2)由题中条件，结合等腰直角三角形性质求出角度及线段长，利用三角形相似的判定与性质代值求解即可得到答案；
(3)当DF与DB重合时，由∠BDC=∠ODK=45∘得点K在DC上，连接OK，如图所示，半圆O与DC所围成的封闭图形的面积为S扇形DOK−S△DOK，求出扇形面积及三角形面积代值即可得到答案．
本题是圆与四边形的综合问题，考查了图形的旋转、圆的相关概念及性质、圆周角定理及推论、等腰直角三角形的性质、三角形相似模型、平行四边形的性质、扇形面积、三角形的面积、解三角形等知识，熟练掌握圆的性质是解决问题的关键．
25.【答案】解：(1)将A，B两点的坐标代入抛物线解析式：
14a+12b+54=0254a+52b+54=0，
解得：a=1，b=3，
∴y=x2−3x+54=(x−32)2−1，
∴M(32,−1)；
(2)①设直线BC的解析式为：y=kx+54，
把B(52,0)代入得：0=52k+54，
解得：k=−12，
∴直线BC的解析式为：y=−12x+54，
∴直线BC平移后的解析式为：y=−12x+n，
把点M(32,−1)代入y=−12x+n，得：−1=−12×32+n，
解得：n=−14，
∴直线DM的解析式为：y=−12x−14，
令y=0，得：x=−12，
∴D(−12,0)，
过点E作EF⊥DM于F，过点M作MH⊥x轴于H，如图：
∴H(32,0)，
∴MH=1，DH=2，
在Rt△DHM中，DM= MH2+DH2= 5，
∵E(76,0)，
∴DE=53，
∵sin∠BDM=HMDM=EFDF，
∴EF= 53，
∴DF= DE2−EF2=2 53，
∴FM=DM−DF= 53，
∴EF=FM，
又∵EF⊥FM，
∴∠DME=45∘；
②把抛物线在x轴下方图象沿x轴翻折得到的新图象，如图：
由平移的性质可知，当直线y=−12x+n在l1和l2之间以及l3上方时，直线与新图象有两个交点，
∵l2的解析式即为直线BC的解析式：y=−12x+54，
∴n2=54，
将A(12,0)代入直线解析式得：0=−12×12+n1，
∴n1=14，
翻折后，AB之间的函数解析式为：y=−x2+3x−54，
与直线解析式联立得：x2−72x+n3+54=0，
此时，一元二次方程有相同的实数根，
∴Δ=(−72)2−4(n3+54)=−4n3+294=0，
∴n3=2916，
∴当直线y=mx+n与新图象有两个公共点时，142916.
【解析】(1)将A，B两点的坐标代入抛物线解析式，求出a和b的值，然后利用配方法求出顶点M的坐标即可；
(2)根据平移的性质，可以求出m的值；
①将M点坐标代入一次函数解析式，求出n的值，过M作x轴垂线，过E作DM垂线，根据三角函数值的定义和勾股定理来求解即可；
②当直线经过A时，有一个公共点，当直线经过B时，有三个公共点，在这之间平移的时候，有两个公共点；当直线与抛物线中间部分相切时，有三个公共点，直线继续向上平移时，有两个公共点，据此解答．
本题主要考查了二次函数综合题，熟练掌握待定系数法求二次函数解析式、待定系数法求一次函数解析式、二次函数的性质、翻折的性质以及二次函数与一元二次方程的关系是本题解题的关键．物质
钨
水银
煤油
水
凝固点
3412℃
−38.87℃
−30℃
0℃
项目
统计量
快递公司
配送速度得分
服务质量得分
平均数
中位数
平均数
中位数
甲
m
8
7
7
乙
8.5
8.5
7
n