2024年中考数学压轴题精选专项突破-一次函数综合

这是一份2024年中考数学压轴题精选专项突破-一次函数综合，共36页。试卷主要包含了选择题，填空题，解答题，实践探究题等内容，欢迎下载使用。
一、选择题（每题3分，共36分）
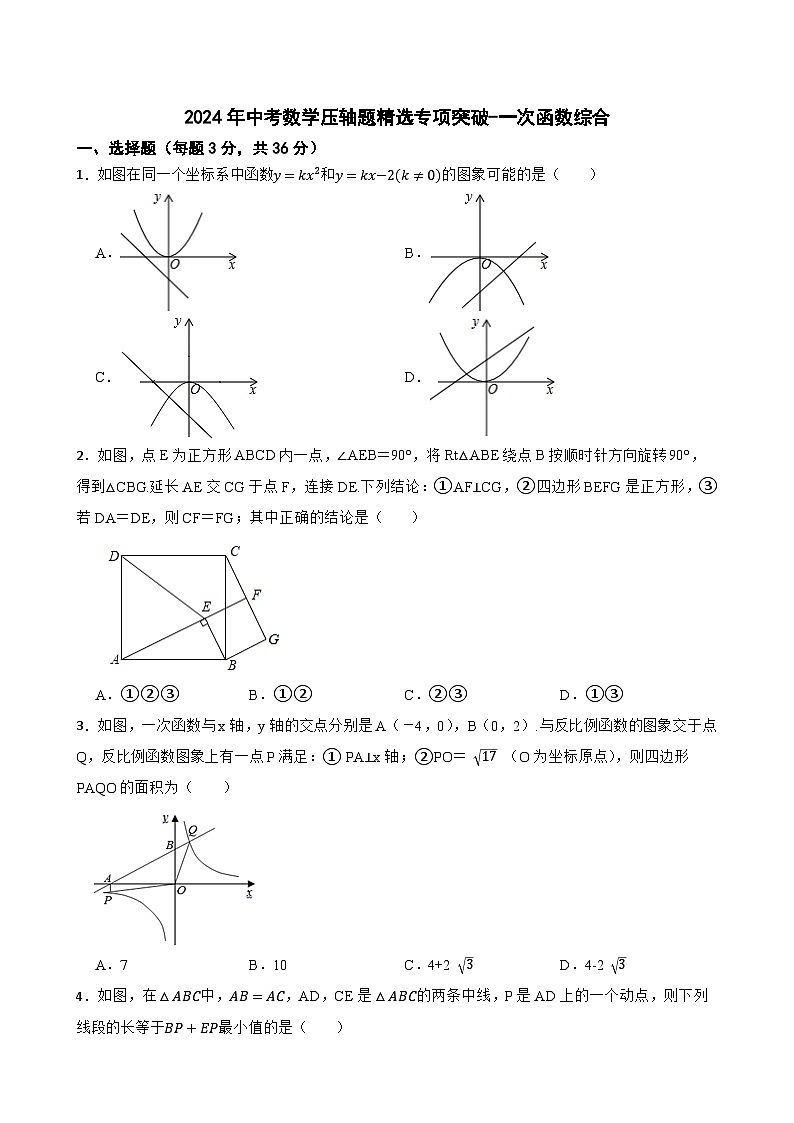
1．如图在同一个坐标系中函数y=kx2和y=kx−2(k≠0)的图象可能的是（ ）
A．B．
C．D．
2．如图，点E为正方形ABCD内一点，∠AEB＝90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBG.延长AE交CG于点F，连接DE.下列结论：①AF⊥CG，②四边形BEFG是正方形，③若DA＝DE，则CF＝FG；其中正确的结论是（ ）
A．①②③B．①②C．②③D．①③
3．如图，一次函数与x轴，y轴的交点分别是A（－4，0），B（0，2）.与反比例函数的图象交于点Q，反比例函数图象上有一点P满足：① PA⊥x轴；②PO＝ 17 （O为坐标原点），则四边形PAQO的面积为（ ）
A．7B．10C．4+2 3D．4-2 3
4．如图，在△ABC中，AB=AC，AD，CE是△ABC的两条中线，P是AD上的一个动点，则下列线段的长等于BP+EP最小值的是（ ）
A．ACB．BCC．ADD．CE
5．甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时，图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图象(线段AB表示甲因故障停车检修)，下列说法正确的个数为（ ）．
①a=240；②b=60；③甲、乙两车第一次相遇的时间是离乙出发3小时；④甲、乙两车相距30km的时间分别为2.5小时、3.5小时、5.5小时、6.5小时．
A．1个B．2个C．3个D．4个
6．如图，正方形ABCD边长为6，AF=BE=2，M、N分别是ED和BF的中点，则MN长为（ ）
A．5B．23C．52D．522
7．在平行四边形ABCD中，AC=4，BD=6，P是BD上的．任一点，过P作EF∥AC，与平行四边形的两条边分别交于点E，F．如图，设BP=x，EF=y，则能反映y与x之间关系的图象为（ ）
A．B．
C．D．
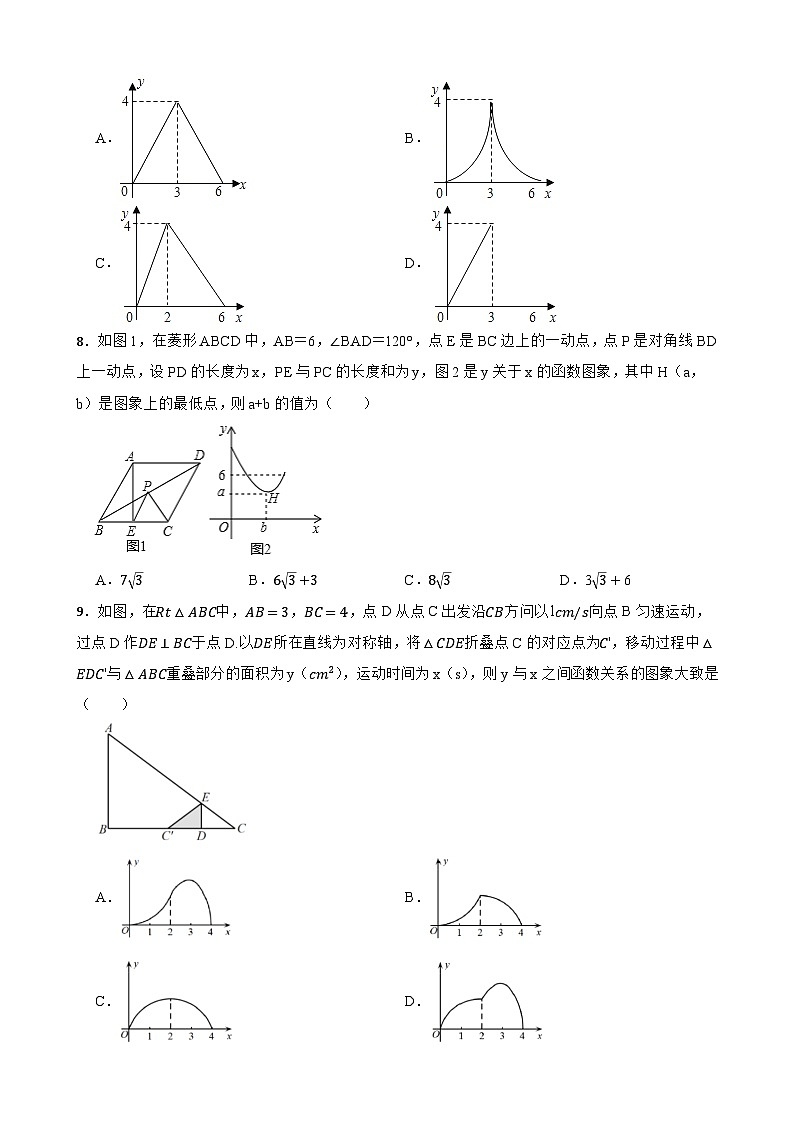
8．如图1，在菱形ABCD中，AB＝6，∠BAD＝120°，点E是BC边上的一动点，点P是对角线BD上一动点，设PD的长度为x，PE与PC的长度和为y，图2是y关于x的函数图象，其中H（a，b）是图象上的最低点，则a+b的值为（ ）
A．73B．63+3C．83D．33+6
9．如图，在Rt△ABC中，AB=3，BC=4，点D从点C出发沿CB方问以lcm/s向点B匀速运动，过点D作DE⊥BC于点D.以DE所在直线为对称轴，将△CDE折叠点C的对应点为C'，移动过程中△EDC'与△ABC重叠部分的面积为y（cm2），运动时间为x（s），则y与x之间函数关系的图象大致是（ ）
A．B．
C．D．
10．在平面直角坐标系内，以原点O为圆心，1为半径作圆，点P在直线y= 3x+23 上运动，过点P作该圆的一条切线，切点为A，则PA的最小值为（ ）
A．3B．2C．D．
11．如图，在△ABC中，∠ACB＝90°，AC＝2，AB＝4，将△ABC绕点C按逆时针方向旋转一定的角度得到△DEC，使得A点恰好落在DE上，则线段BD的长为（ ）
A．23B．5C．27D．33
12．如图，在直角坐标系中，等腰直角△ABO的O点是坐标原点，A的坐标是（﹣4，0），直角顶点B在第二象限，等腰直角△BCD的C点在y轴上移动，我们发现直角顶点D点随之在一条直线上移动，这条直线的解析式是（ ）
A．y=﹣2x+1B．y=﹣ x+2
C．y=﹣3x﹣2D．y=﹣x+2
二、填空题（每题3分，共18分）
13．如图，在平面直角坐标系中，已知直线 y=x+1 和双曲线 y=−1x ，在直线上取一点，记为 A1 ，过 A1 作 x 轴的垂线交双曲线于点 B1 ，过 B1 作y轴的垂线交直线于点 A2 ，过 A2 作x轴的垂线交双曲线于点 B2 ，过 B2 作 y 轴的垂线交直线于点 A3， ······，依次进行下去，记点 An 的横坐标为 an ，若 a1=2， 则 a2020= ．
14．如图所示，从高为2m的点 A 处向右上抛一个小球 P ，小球路线呈抛物线 L 形状，小球水平经过2m时达到最大高度6m，然后落在下方台阶B处弹起，已知 MN=4 m， FM=DE=BC=1.2 m， CD=EF=1 m，若小球弹起形成一条与 L 形状相同的抛物线，且落点 Q 与 B ， D 在同一直线上，则小球弹起时的最大高度是 m
15．如图，四边形ABCD为正方形纸片，E是边CB的中点，连接DE，P是边CD上一点，将纸片沿着AP折叠，使点D落在DE上的F点处，则DFEF为 ．
16．在平面直角坐标系中，正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2、正方形A4B4C4C3、…、正方形AnBn∁nCn-1按如图所示的方式放置，其中点A1，A2，A3，A4，…，An均在一次函数y＝kx+b的图象上，点C1，C2，C3，C4，…，∁n均在x轴上．若点B1的坐标为（1，1），点B2的坐标为（3，2），则点An的坐标为 ．
17．如图，四边形ABCD是正方形，△BPC是等边三角形，延长BP，CP分别交AD于点E，F，连接BD，DP，BD与CF相交于点H，给出下列结论：①AE=12BE；②∠CPD=75°；③△PDE∽△DBE；④ED2=EP⋅PB；其中正确的是 。（只填写序号即可）
18．如图，点O为等边三角形△ABC的中心，点D，E，F分别在边AB，BC，AC上，将AB，BC，AC分别沿着线段AE，BF，CD翻折，得到AB'，BC'，CA'，且恰好都经过点O.AE与CD交于点G，与BF交于点H，CD与BF交于点I.
（1）若BC=2，则CF= ；
（2）设△GHI的面积为S1，△ABC的面积为S2，则S1S2= .
三、解答题（共5题，共38分）
19．已知：等边△ABC，CE∥AB，D为BC上一点，且∠ADE=60°，求证：△ADE是等边三角形.
20．如图，四边形OABC是矩形，点A、C在坐标轴上，△ODE是由△OCB绕点O顺时针旋转90°得到的，点D在x轴上，直线BD交y轴于点F，交OE于点H，线段BC、OC的长是方程x2-6x+8=0的两个根，且OC＞BC.
（1）求直线BD的解析式.
（2）求△OFH的面积.
（3）点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由.
21．如图，在平面直角坐标系中，点 B在第一象限，BA⊥x轴于点A，BC⊥y轴于点C，BA=3，BC=5，有一反比例函数的图象刚好经过点 B.
（1）分别求出该反比例函数的表达式和直线 AC 的函数表达式.
（2）动点P 在射线CA(不与点C重合)上，过点 P 作直线l⊥x轴，交反比例函数图象于点 D.在坐标平面内，是否存在这样的点Q，使得以点 B，D，P，Q为顶点的四边形为菱形? 若存在，求出点 Q 的坐标；若不存在，请说明理由.
22．某环形道路上顺时针排列着4所中学：A1，A2，A3，A4，它们顺次有彩电15台，8台，5台，12台．为使各校的彩电数相同，允许一些中学向相邻中学调出彩电．问怎样调配才能使调出的彩电台数最小？并求调出彩电的最小总台数．
23．在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC，连结OB，D为OB的中点。点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF。已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒。
（1）如图1，当t=3时，求DF的长；
（2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值；
（3）连结AD，当AD将△DEF分成的两部分面积之比为1：2时，求相应t的值。
四、实践探究题（共8分）
24． 如图
（1）观察猜想：
如图1，在直角△ABC中，∠BAC=90°，AB=AC，点D为BC边上一动点（与点B不重合），连接AD，将△ABD绕点A逆时针旋转90°到△ACE，那么CE、BD之间的位置关系为 ，数量关系为 ；
（2）数学思考：
如图2，在△ABC中，∠CAB=90°，AB=AC，D、E为BC上两点，且∠DAE=45°，求证：BD2+CE2=DE2．
（3）拓展延伸：
如图3，在△ABC中，∠CAB=120°，AB=AC，∠DAE=60°，若以BD、DE、EC为边的三角形是以BD为斜边的直角三角形，当BD=2时，求DE的长．
答案解析部分
1．【答案】C
【解析】【解答】解：根据二次函数、一次函数的图象与系数k的性质进行分类讨论，可得：
当k>0时：函数 y=kx2 （k≠0）开口向上，顶点为原点， y=kx−2(k≠0)的图象经过一、三、四象限；
当k0与k