2024年山东省淄博市淄川区中考二模数学试题

这是一份2024年山东省淄博市淄川区中考二模数学试题，共10页。试卷主要包含了评分以答题卡上的答案为依据等内容，欢迎下载使用。
注意事项：
1．答题前，考生务必用0.5毫米黑色签字笔将学校、姓名、考试号、座号填写在答题卡和试卷规定位置，并核对条形码．
2．选择题每小题选出答案后，用2B铅笔涂黑答题卡对应题目的答案标号；如需改动，用橡皮擦干净后，再选涂其他答案标号．
3．解答题必须用0.5毫米黑色签字笔作答，字体工整、笔迹清晰，写在答题卡各题目指定区域内；如需改动，先划掉原来答案，然后再写上新答案．严禁使用涂改液、胶带纸修正带修改．不允许使用计算器．
4．保证答题卡清洁、完整，严禁折叠，严禁在答题卡上做任何标记．
5．评分以答题卡上的答案为依据．不按以上要求作答的答案无效．
一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中只有一个是符合题目要求的．
1．若的相反数是2024，则的值为（ ）
A．2024B．C．D．
2．如图，正方形网格中每个小正方形的边长都为1，则与的大小关系为（ ）
A．B．C．D．无法比较
3．下列运算错误的是（ ）
A．B．
C．D．
4．由方程组，可得出与之间的关系是（ ）
A．B．C．D．
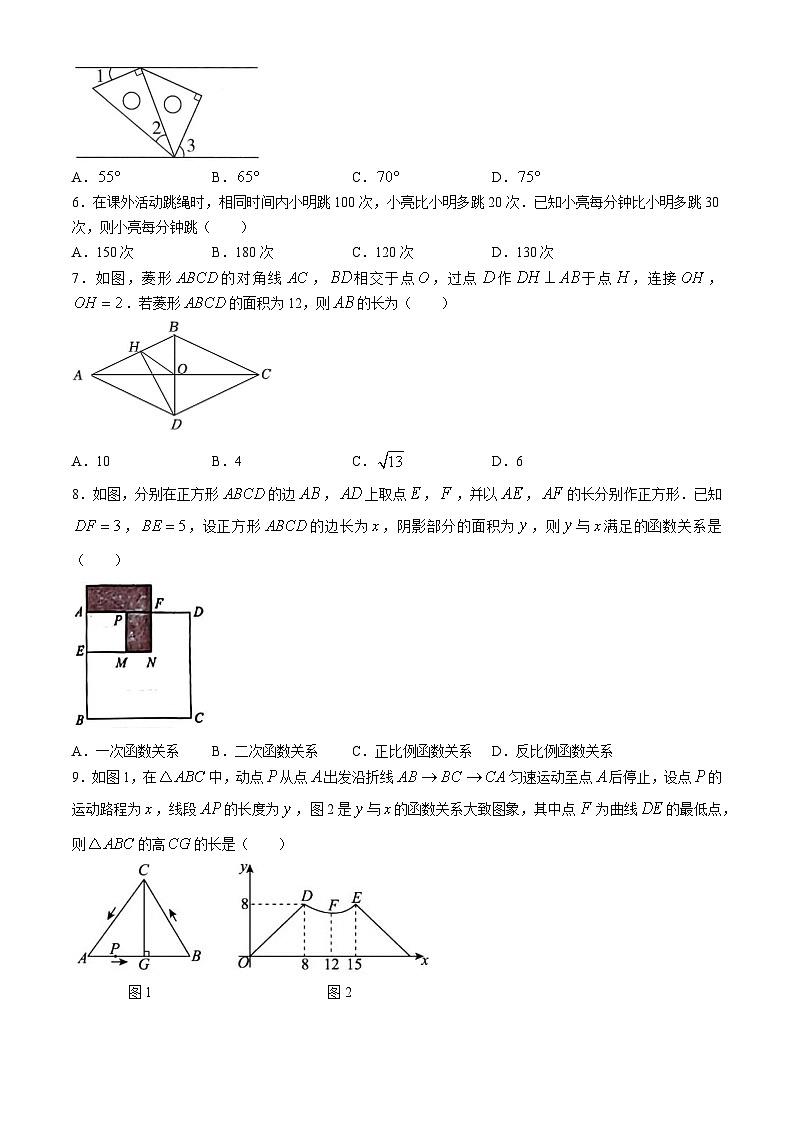
5．将一副三角板按如图所示放置在一组平行线内，，，则等于（ ）
A．B．C．D．
6．在课外活动跳绳时，相同时间内小明跳100次，小亮比小明多跳20次．已知小亮每分钟比小明多跳30次，则小亮每分钟跳（ ）
A．150次B．180次C．120次D．130次
7．如图，菱形的对角线，相交于点，过点作于点，连接，．若菱形的面积为12，则的长为（ ）
A．10B．4C．D．6
8．如图，分别在正方形的边，上取点，，并以，的长分别作正方形．已知，，设正方形的边长为，阴影部分的面积为，则与满足的函数关系是（ ）
A．一次函数关系B．二次函数关系C．正比例函数关系D．反比例函数关系
9．如图1，在中，动点从点出发沿折线匀速运动至点后停止，设点的运动路程为，线段的长度为，图2是与的函数关系大致图象，其中点为曲线的最低点，则的高的长是（ ）
图1 图2
A．B．C．D．
10．已知二次函数的图象经过点，，，，，，则函数值，，的大小关系是（ ）
A．B．C．D．
二、填空题：本大题共5小题，满分20分．只要求填写最后结果，每小题填对得4分．
11．一副三角板中，除直角外最大的锐角是__________度．
12．若与的和是单项式，则的平方根为__________．
13．小慧去花店购买鲜花，若买5支玫瑰和3支百合，则她所带的钱还剩下10元；若买3支玫瑰和5支百合，则她所带的钱还缺4元．若只买8支玫瑰，则她所带的钱还剩个__________元．
14．如图，在中，，，将绕点顺时针旋转后得到，则边在旋转过程中所扫过的图形的面积为__________．
15．观察下边的数表（横排为行，竖排为列），按数表中的规律，分数若排在第行列，则的值为__________．
……
三、解答题：本大题共8小题，共90分．解答要写出必要的文字说明、证明过程或演算步骤．
16．（本题满分10分）
（1）分解因式：；（2）化简：．
17．（本题满分10分）
如图，在和中，点，，，在同一条直线上，给出下列条件：
①；②；③；④．请用其中三个作为条件，余下一个作为结论，编一道真命题，并说明理由．
条件为__________（填序号），结论为__________（填序号）．
18．（本题满分10分）
汽车盲区是指驾驶员位于驾驶座位置，其视线被车体遮挡而不能直接观察到的区域．如图，，分别为汽车两侧盲区的示意图，已知视线与地面的夹角，视线与地面的夹角，点，分别为，与车窗底部的交点，，，垂直地面，点到点的距离．
（1）求盲区中的长度；
（2）点在上，，在处有一个高度为的物体，驾驶员能观察到物体吗？请说明理由．
（参考数据：，，，）
19．（本题满分10分）
教育部下发的《关于进一步加强中小学生睡眠管理工作的通知》要求，初中生每天睡眠时间应达到9小时．为了解学生每天的睡眠时间，学校随机调查了部分学生，将学生睡眠时间分为，，，四组（每名学生必须选择且只能选择一种情况）：
组：睡眠时间小时；组；8小时睡眠时间小时；
组：9小时睡眠时间小时；组：睡眠时间小时；
如图1和图2是根据调查结果绘制的不完整的统计图．
图1 图2
请根据图中提供的信息，解答下列问题：
（1）被调查的学生有__________人；
（2）补全条形统计图；
（3）请估计全校800名学生中睡眠时间不足9小时的人数．
20．（本题满分12分）
已知关于的一元二次方程．
（1）求证：该一元二次方程总有两个不相等的实数根；
（2）若该方程的两个根，是一个矩形的一边长和对角线的长，且矩形的另一边长为3，试求的值．
21．（本题满分12分）
如图，在四边形中，，，顶点，分别在轴，轴上，反比例函数的图象经过点，点．
（1）求反比例函数的解析式；
（2）请用无刻度的直尺和圆规做出线段的垂直平分线；（要求：不写作法，保留作图痕迹）
（3）线段与（2）中所作的垂直平分线交于点，直接写出点的坐标．
22．（本题满分13分）
如图，在中，，，点是平面内不与点，重合的任意一点，连接，将线段绕点顺时针旋转得到线段，连接，．
（1）观察猜想如图1，当时，线段，之间的数量关系，并说明理由；
（2）类比探究如图2．当时，请写出线段，之间的数量关系，并仅就图2的情形说明理由；
（3）拓展应用如图3，当，，点，与的中点三点共线时，请直接写出的值．
图1 图2 图3
23．（本题满分13分）
如图，已知抛物线与轴交于点，，与轴交于点，对称轴为．
（1）求抛物线函数解析式；
（2）如图1，若点是线段上的一个动点（不与点，重合），过点作轴的平行线交抛物线于点，连接．当线段长度最大时，判断四边形的形状，并说明理由；
（3）如图2，在（2）的条件下，是的中点，过点的直线与抛物线交于点，且．在轴上是否存在点，使得为等腰三角形？若存在，求出点的坐标；若不存在，请说明理由．
图1 图2
初四数学答案及评分建议
一、选择题：每小题4分，计40分．
1．D2．A3．C4．B5．C
6．B7．C8．A9．D10．D
二、填空题：每小题填对得4分．
11．6012．13．3114．15．2023
三、解答题．
16．（本题满分10分）
解：（1）
（2）
17．（本题满分10分）
略．填上序号且对，得4分．说明理由得6分，共计10分．
18．（本题满分10分）
解：（1）在中，（米）．
根据图形，易得四边形为矩形，所以米．
在中，（米）；
所以盲区中的长度为2.8米．
（2）驾驶员不能观察到该物体．理由如下：
过点作交于点．
∵，，∴．
在中，（米）．
因为，所以驾驶员不能观察到物体．
19．（本题满分10分）
解：（1）200；
（2）略；
（3）320．
20．（本题满分12分）
解：（1）方程变形，得：，
∵，
∴该一元二次方程总有两个不相等的实数根．
（2）方程的实数根为：，∴，，
∵，∴只能作为矩形的对角线长．根据勾股定理可得：
，解得．
21．（本题满分12分）
解：（1）过点轴于点．
∵，，∴，．
易得，
又∵，∴，∴，．
所以点的坐标为．
把代入得：，
所以反比例函数的解析式为；
（2）略；
（3）．
22．（本题满分13分）
解：（1）．
理由如下：
连接．∵，∴，均为等边三角形，
∴，，，
∴，∴，∴．
（2）．
理由如下：
连接．∵，∴，均为等腰直角三角形．
∴，，∴．
又∵，∴，
∴，∴，∴；
（3）或．
解析：在中，，，
∴，．
在中，，∴．
分情况讨论：
（1）当点在直线上方时，连接．类比（2）易得，
∴，∴，∴，∴；
（2）当点在直线下方时，连接．类比（2）易得，
∴，∴，∴，∴．
23．（本题满分13分）
解：（1）把代入，得：；
因为对称轴为，所以；
∴∴，，
所以抛物线的函数表达式为．
（2）四边形是平行四边形．
理由如下：
易得直线的解析式为，设点，∴．
∴，∵，∴有最大值，此时
，．∴，又∵，∴，又∵，
∴四边形是平行四边形．
（3）过点作于点，设交于点．
易得，，∴，∴．
易得．易得，
所以直线的解析式为．
易得点，∴．
设点．
当时，，∴；
当时，，方程无解；
当时，，∴．
故点的坐标为或或．