资料中包含下列文件,点击文件名可预览资料内容













还剩37页未读,
继续阅读
所属成套资源:新人教a版数学必修第一册PPT课件+分层作业(含解析)
成套系列资料,整套一键下载
第三章 函数的概念与性质(单元复习课)PPT+分层作业+答案解析
展开
这是一份第三章 函数的概念与性质(单元复习课)PPT+分层作业+答案解析,文件包含第三章函数的概念与性质单元复习课件pptx、第三章函数的概念与性质单元测试卷原卷版docx、第三章函数的概念与性质单元测试卷解析版docx等3份课件配套教学资源,其中PPT共45页, 欢迎下载使用。
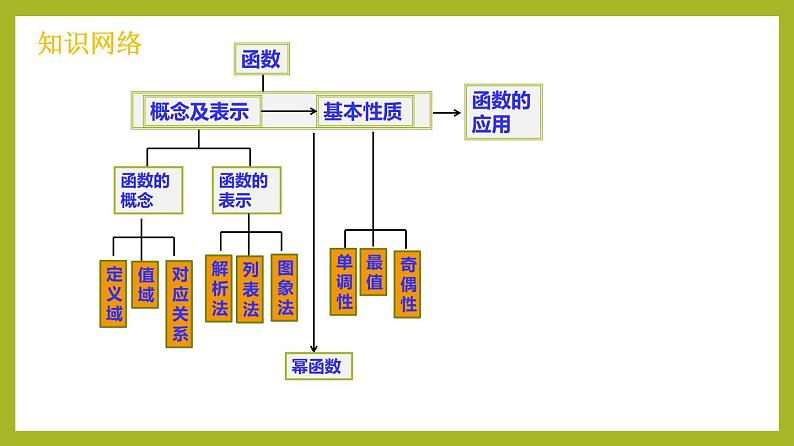
人教A版2019必修第一册第三章 函数的概念与性质单元复习课件学习目标1.掌握函数的概念;2.了解分段函数,会画分段函数的图像;3.理解函数性质并且熟练运用;4.能用函数与方程的思想解决实际问题.定义域值域对应关系解析法列表法图象法单调性最值奇偶性知识网络一、基础知识整合1.函数的概念一般地,设A,B是两个非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有 f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个________,记作y=f(x),x∈A,其中,x叫做________,x的取值范围A叫做函数的 ;与x的值相对应的y值叫做________,其集合{f(x)|x∈A}叫做函数的________.唯一确定的数函数自变量定义域函数值值域2.函数的表示方法(1)解析法:就是用_____ ___表示两个变量之间的对应关系的方法.(2)图象法:就是用__ ______表示两个变量之间的对应关系的方法.(3)列表法:就是__ ______来表示两个变量之间的对应关系的方法.3.构成函数的三要素(1)函数的三要素是:________,________,________.(2)两个函数相等:如果两个函数的________相同,并且________完全一致,则称这两个函数相等. 数学表达式图象列出表格定义域对应关系值域定义域对应关系(3).求函数的定义域应注意:② f(x)是分式,则分母不为0;① f(x)是整式,则定义域是R;③ 偶次方根的被开方数非负;表格形式给出时,定义域就是表格中数的集合.4.分段函数若函数在定义域的不同子集上的对应关系也不同,这种形式的函数叫做分段函数,它是一类重要的函数. 5. 函数的单调性(1)增函数与减函数一般地,设函数f(x)的定义域为I: ①如果对于定义域I内某个区间D上的 自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说函数f(x)在区间D上是 .②如果对于定义域I内某个区间D上的 自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说函数f(x)在区间D上是 .(2)单调性与单调区间如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的) ,区间D叫做y=f(x)的 . 任意两个增函数任意两个减函数单调性单调区间(1).偶函数的定义: 如果对于函数f(x)的定义域内任意一个x都有f(-x)=f(x),那么函数f(x)就叫做偶函数.(2).奇函数的定义: 如果对于函数f(x)的定义域内任意一个x都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.(3).几个结论:①偶函数的图象关于y轴对称.②奇函数的图象关于原点对称.③函数y=f(x)是奇函数或偶函数的一个必不可少的条件是---定义域关于原点对称,否则它是非奇非偶函数. ④判断一个函数是否为奇(偶)函数还可用f(-x)±f(x)=0 或 .6.奇偶函数定义7.常见幂函数的性质 函数性质RRRRR[0,+∞)[0,+∞)[0,+∞)奇奇奇偶非奇非偶[0,+∞)增(-∞,0]减(0,+∞)减(-∞,0)减增增增(1,1)题型一 求函数的定义域求函数定义域的类型与方法(1)已给出函数解析式:函数的定义域是使解析式有意义的自变量的取值集合.(2)实际问题:求函数的定义域既要考虑解析式有意义,还应考虑使实际问题有意义.(3)复合函数问题:①若f(x)的定义域为[a,b],f(g(x))的定义域应由a≤g(x)≤b解出;②若f(g(x))的定义域为[a,b],则f(x)的定义域为g(x)在[a,b]上的值域.注意:a.f(x)中的x与f(g(x))中的g(x)地位相同;b.定义域是指x的范围.二、题型分类讲解答案 (1)D (2)由y=f(x-1)的定义域是[-1,2],则x-1∈[-2,1],即f(x)的定义域是[-2,1],令-2≤1-3x≤1,解得0≤x≤1,即y=f(1-3x)的定义域为[0,1].答案 (2)C(2)已知函数y=f(x-1)的定义域是[-1,2],则y=f(1-3x)的定义域为( )A. B.C.[0,1] D.【训练1】 若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2,值域为{1,4}的“同族函数”共有( ) A.7个 B.8个 C.9个 D.10个 解析 由题意知,问题的关键在于确定函数定义域的个数.函数解析式为y=x2,值域为{1,4}, 当x=±1时,y=1;当x=±2时,y=4, 则定义域可以为{1,2},{1,-2},{-1,2},{-1,-2},{1,-1,2},{1,-1,-2},{-1,2,-2},{1,-2,2},{1,-1,2,-2},因此“同族函数”共有9个. 答案 C题型二 求函数的解析式【例2】 (1)已知f(x-1)=2x+5,则f(x)的解析式为________. 解析 (1)法一(换元法) 设x-1=t,则x=t+1,∴f(t)=2(t+1)+5=2t+7,∴f(x)=2x+7.法二(配凑法) f(x-1)=2x+5=2(x-1)+7,所以f(x)=2x+7,即函数的解析式为f(x)=2x+7.(2)设f(x)是定义在R上的函数,且满足f(0)=1,并且x,y∈R,都有f(x-y)=f(x)-y(2x-y+1),则f(x)=________.(2)法一 由已知条件得f(0)=1,又f(x-y)=f(x)-y(2x-y+1),设y=x,则f(x-y)=f(0)=f(x)-x(2x-x+1)=1,所以f(x)=x2+x+1.法二 令x=0,得f(0-y)=f(0)-y(-y+1),即f(-y)=1-y(-y+1),将-y 用x代换得f(x)=x2+x+1.答案 (1)f(x)=2x+7 (2)x2+x+1【训练2】 根据如图所示的函数f(x)的图象,写出函数的解析式.当1≤x<2时,f(x)=1.题型三 分段函数1.求分段函数的函数值的方法:先确定要求值的自变量的取值属于哪一段区间,然后代入该段的解析式求值.当出现f(f(a))的形式时,应从内到外依次求值.2.已知分段函数的函数值,求自变量的值的方法:先假设自变量的值在分段函数定义域的各段上,然后求出相应自变量的值,切记要检验.3.在分段函数的前提下,求某条件下自变量的取值范围的方法:先假设自变量的值在分段函数定义域的各段上,然后求出在相应各段定义域上自变量的取值范围,再求它们的并集即可.当a>1时,a+1>2,∴f(a)=2(a-1),f(a+1)=2(a+1-1)=2a,∴2(a-1)=2a,无解.当a=1时,a+1=2,f(1)=0,f(2)=2,不符合题意.答案 C答案 (1)B (2)当a≤-2时,f(a)=a<-3,此时不等式的解集是(-∞,-3);当-21,x1x2-1>0,∴f(x1)-f(x2)<0,即f(x1)0,所以f(-x)=-(-x)2+2(-x)=-x2-2x.又f(x)为奇函数,所以f(-x)=-f(x),所以x<0时,f(x)=x2+2x=x2+mx,所以m=2.(2)要使f(x)在[-1,a-2]上单调递增,所以10时,①图象都通过点(0,0),(1,1);②在第一象限内,函数值随x的增大而增大;③在第一象限内,α>1时,图象是向下凸上升的;0<α<1时,图象是向上凸上升的;④在第一象限内,过点(1,1)后,图象向右上方无限伸展.(2)当α<0时,①图象都通过点(1,1);②在第一象限内,函数值随x的增大而减小,图象是向下凸的;③在第一象限内,图象向上与y轴无限接近,向右与x轴无限接近;④在第一象限内,过点(1,1)后,|α|越大,图象下降的速度越快.解 (1)由已知f(x)在(0,+∞)上是增函数,又p∈N,因而p=0或1或2.当p=1时,f(x)=x2,符合题意.(2)由(1)知g(x)=-qf(f(x))+(2q-1)f(x)+1=-qf2(x)+(2q-1)f(x)+1.f(x)=x2≥0,因而,当x∈(-∞,-4]时,f(x)=x2∈[16,+∞);当x∈(-4,0)时,f(x)=x2∈(0,16).解 (1)幂函数f(x)=x-m2+2m+3(m∈Z)为偶函数,且在(0,+∞)上是增函数,则-m2+2m+3为偶数,且-m2+2m+3>0,得-12恒成立,则c-1>2,即c>3.故实数c的取值范围为(3,+∞).解 (1)因为甲大棚投入50万元,则乙大棚投入150万元,所以投入甲大棚128万元,乙大棚72万元时,总收益最大,且最大收益为282万元.【训练6】 为纪念重庆黑山谷晋升国家5A级景区五周年,特发行黑山谷纪念邮票,从2017年11月1日起开始上市.通过市场调查,得到该纪念邮票在一周内每1张的市场价y(单位:元)与上市时间x(单位:天)的数据如下:(1)分析上表数据,说明黑山谷纪念邮票的市场价y(单位:元)与上市时间x(单位:天)的变化关系,并判断y与x满足下列哪种函数关系,①一次函数;②二次函数;③幂函数,并求出函数的解析式;(2)利用你选取的函数,求黑山谷纪念邮票市场价最低时的上市天数及最低的价格.解 (1)由于市场价y随上市时间x的增大先减小后增大,而模型①③均为单调函数,不符合题意,故选择二次函数模型②,设f(x)=ax2+bx+c(a≠0)由表中数据可知∴f(x)=x2-6x+10(x>0),(2)由(1)知f(x)=x2-6x+10=(x-3)2+1,当x=3时,黑山谷纪念邮票市场价最低,最低为1元,故黑山谷纪念邮票市场价最低时的上市为第3天,最低的价格为1元.DA随堂检测
人教A版2019必修第一册第三章 函数的概念与性质单元复习课件学习目标1.掌握函数的概念;2.了解分段函数,会画分段函数的图像;3.理解函数性质并且熟练运用;4.能用函数与方程的思想解决实际问题.定义域值域对应关系解析法列表法图象法单调性最值奇偶性知识网络一、基础知识整合1.函数的概念一般地,设A,B是两个非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有 f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个________,记作y=f(x),x∈A,其中,x叫做________,x的取值范围A叫做函数的 ;与x的值相对应的y值叫做________,其集合{f(x)|x∈A}叫做函数的________.唯一确定的数函数自变量定义域函数值值域2.函数的表示方法(1)解析法:就是用_____ ___表示两个变量之间的对应关系的方法.(2)图象法:就是用__ ______表示两个变量之间的对应关系的方法.(3)列表法:就是__ ______来表示两个变量之间的对应关系的方法.3.构成函数的三要素(1)函数的三要素是:________,________,________.(2)两个函数相等:如果两个函数的________相同,并且________完全一致,则称这两个函数相等. 数学表达式图象列出表格定义域对应关系值域定义域对应关系(3).求函数的定义域应注意:② f(x)是分式,则分母不为0;① f(x)是整式,则定义域是R;③ 偶次方根的被开方数非负;表格形式给出时,定义域就是表格中数的集合.4.分段函数若函数在定义域的不同子集上的对应关系也不同,这种形式的函数叫做分段函数,它是一类重要的函数. 5. 函数的单调性(1)增函数与减函数一般地,设函数f(x)的定义域为I: ①如果对于定义域I内某个区间D上的 自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说函数f(x)在区间D上是 .②如果对于定义域I内某个区间D上的 自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说函数f(x)在区间D上是 .(2)单调性与单调区间如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的) ,区间D叫做y=f(x)的 . 任意两个增函数任意两个减函数单调性单调区间(1).偶函数的定义: 如果对于函数f(x)的定义域内任意一个x都有f(-x)=f(x),那么函数f(x)就叫做偶函数.(2).奇函数的定义: 如果对于函数f(x)的定义域内任意一个x都有f(-x)=-f(x),那么函数f(x)就叫做奇函数.(3).几个结论:①偶函数的图象关于y轴对称.②奇函数的图象关于原点对称.③函数y=f(x)是奇函数或偶函数的一个必不可少的条件是---定义域关于原点对称,否则它是非奇非偶函数. ④判断一个函数是否为奇(偶)函数还可用f(-x)±f(x)=0 或 .6.奇偶函数定义7.常见幂函数的性质 函数性质RRRRR[0,+∞)[0,+∞)[0,+∞)奇奇奇偶非奇非偶[0,+∞)增(-∞,0]减(0,+∞)减(-∞,0)减增增增(1,1)题型一 求函数的定义域求函数定义域的类型与方法(1)已给出函数解析式:函数的定义域是使解析式有意义的自变量的取值集合.(2)实际问题:求函数的定义域既要考虑解析式有意义,还应考虑使实际问题有意义.(3)复合函数问题:①若f(x)的定义域为[a,b],f(g(x))的定义域应由a≤g(x)≤b解出;②若f(g(x))的定义域为[a,b],则f(x)的定义域为g(x)在[a,b]上的值域.注意:a.f(x)中的x与f(g(x))中的g(x)地位相同;b.定义域是指x的范围.二、题型分类讲解答案 (1)D (2)由y=f(x-1)的定义域是[-1,2],则x-1∈[-2,1],即f(x)的定义域是[-2,1],令-2≤1-3x≤1,解得0≤x≤1,即y=f(1-3x)的定义域为[0,1].答案 (2)C(2)已知函数y=f(x-1)的定义域是[-1,2],则y=f(1-3x)的定义域为( )A. B.C.[0,1] D.【训练1】 若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2,值域为{1,4}的“同族函数”共有( ) A.7个 B.8个 C.9个 D.10个 解析 由题意知,问题的关键在于确定函数定义域的个数.函数解析式为y=x2,值域为{1,4}, 当x=±1时,y=1;当x=±2时,y=4, 则定义域可以为{1,2},{1,-2},{-1,2},{-1,-2},{1,-1,2},{1,-1,-2},{-1,2,-2},{1,-2,2},{1,-1,2,-2},因此“同族函数”共有9个. 答案 C题型二 求函数的解析式【例2】 (1)已知f(x-1)=2x+5,则f(x)的解析式为________. 解析 (1)法一(换元法) 设x-1=t,则x=t+1,∴f(t)=2(t+1)+5=2t+7,∴f(x)=2x+7.法二(配凑法) f(x-1)=2x+5=2(x-1)+7,所以f(x)=2x+7,即函数的解析式为f(x)=2x+7.(2)设f(x)是定义在R上的函数,且满足f(0)=1,并且x,y∈R,都有f(x-y)=f(x)-y(2x-y+1),则f(x)=________.(2)法一 由已知条件得f(0)=1,又f(x-y)=f(x)-y(2x-y+1),设y=x,则f(x-y)=f(0)=f(x)-x(2x-x+1)=1,所以f(x)=x2+x+1.法二 令x=0,得f(0-y)=f(0)-y(-y+1),即f(-y)=1-y(-y+1),将-y 用x代换得f(x)=x2+x+1.答案 (1)f(x)=2x+7 (2)x2+x+1【训练2】 根据如图所示的函数f(x)的图象,写出函数的解析式.当1≤x<2时,f(x)=1.题型三 分段函数1.求分段函数的函数值的方法:先确定要求值的自变量的取值属于哪一段区间,然后代入该段的解析式求值.当出现f(f(a))的形式时,应从内到外依次求值.2.已知分段函数的函数值,求自变量的值的方法:先假设自变量的值在分段函数定义域的各段上,然后求出相应自变量的值,切记要检验.3.在分段函数的前提下,求某条件下自变量的取值范围的方法:先假设自变量的值在分段函数定义域的各段上,然后求出在相应各段定义域上自变量的取值范围,再求它们的并集即可.当a>1时,a+1>2,∴f(a)=2(a-1),f(a+1)=2(a+1-1)=2a,∴2(a-1)=2a,无解.当a=1时,a+1=2,f(1)=0,f(2)=2,不符合题意.答案 C答案 (1)B (2)当a≤-2时,f(a)=a<-3,此时不等式的解集是(-∞,-3);当-2
相关资料
更多










