安徽省亳州市涡阳县多校联考2024年中考数学三模试题

这是一份安徽省亳州市涡阳县多校联考2024年中考数学三模试题，共8页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

第Ⅰ卷 客观题
第Ⅰ卷的注释
一、选择题（本大题共10小题，每小题4分，满分40分。每小题都给出A、B、C、D四个选项，其中只有一个是符合题目要求的）(共10题；共40分)
1. 下列各数中，最小的数是（ ）
2. 据统计，2023年合肥市的生产总值为12673.8亿元，其中12673.8亿用科学记数法表示为（ ）
3. 计算的结果是（ ）
4. 下图是由一个长方体截去了一部分得到的几何体，则俯视图是（ ）
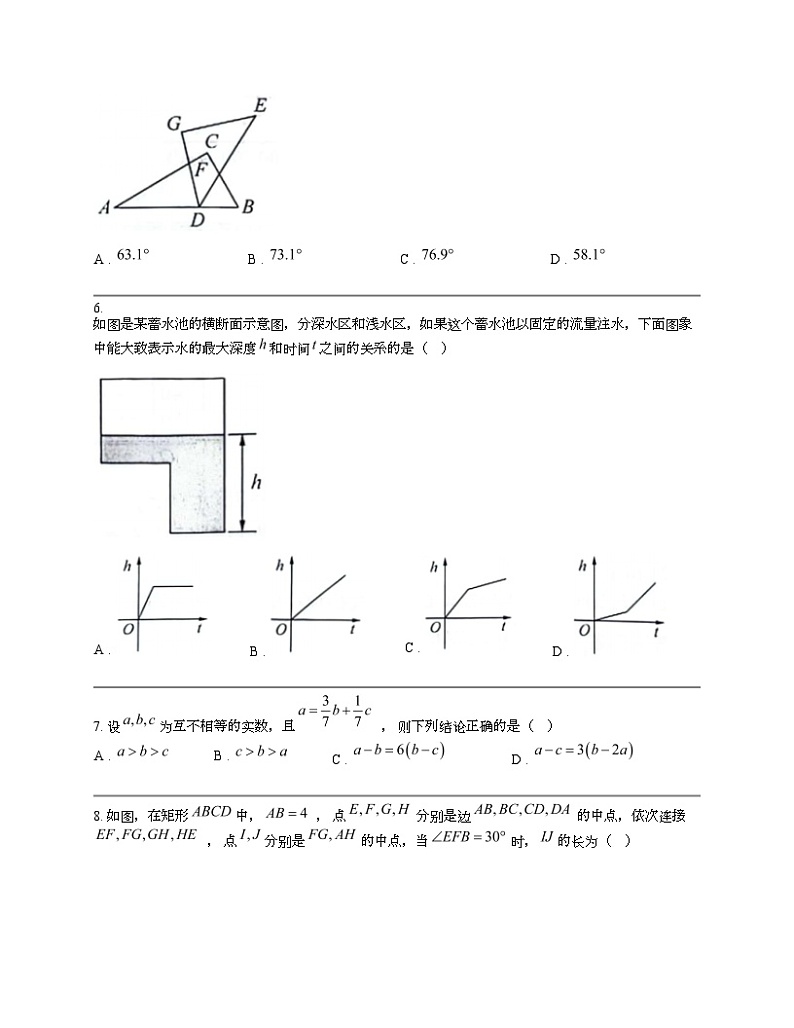
5. 两个直角三角板如图摆放，其中 ， ， ， 与交于点 ． 若 ， 则的大小为（ ）
6. 如图是某蓄水池的横断面示意图，分深水区和浅水区，如果这个蓄水池以固定的流量注水，下面图象中能大致表示水的最大深度和时间之间的关系的是（ ）
7. 设为互不相等的实数，且 ， 则下列结论正确的是（ ）
8. 如图，在矩形中， ， 点分别是边的中点，依次连接 ， 点分别是的中点，当时，的长为（ ）
9. 某公司楼顶公益广告牌上“大湖名城”四个字是霓虹灯，四个字一个接一个亮起来（亮后不熄灭），直至全部亮起来再循环（不考虑其他因素对灯的影响），当路人一眼望去，能够看到四个字全亮的概率是（ ）
10. 在矩形中， ， ， 是边上的点，将沿着对折，当点落在矩形对角线上时，则（ ）
二、填空题（本大题共4小题，每小题5分，满分20分）(共4题；共20分)
11. 计算：____________________．
12. 因式分解：____________________．
13. 如图，的半径为1，四边形内接于 ， 是的直径，若 ， ， 则____________________．
14. 在平面直角坐标系中，已知抛物线与轴交于 ， 两点（点在点的左侧），与轴交于点 ， 顶点为点 ．
①该抛物线的对称轴为____________________；
②若 ， 点坐标为 ， 直线与轴交于点 ， 则____________________．
第Ⅱ卷 主观题
第Ⅱ卷的注释
三、（本大题共2小题，每小题8分，满分16分）(共2题；共16分)
15. 解不等式： ．
16. 如图，在每个小正方形的边长为1个单位的网格中，的顶点均在格点（网格线的交点）上．
（1） 将向上平移5个单位得到 ， 画出；
（2） 将绕点顺时针旋转得到 ， 画出 ．
四、（本大题共2小题，每小题8分，满分16分）(共2题；共16分)
17. 某校数学社团的同学们欲测量斜拉桥的高度（如图1），他们在地面上架设测角仪 ， 先在点处测斜拉桥最高点的仰角 ， 然后沿方向前进到达点处，并测出点的仰角 ， 测角仪高度（如图2）．已知 ， ， ， ， 计算斜拉桥的高度 ． （结果精确到 ． 参考数据： ， ， ， ）
图1 图2
18. 如图是由一些火柴棒搭成的图案：
（1） 摆第①个图案用____________________根火柴棒，摆第②个图案用____________________根火柴棒，摆第③个图案用____________________根火柴棒；
（2） 按照这种方式摆下去，摆第个图案用多少根火柴棒？
（3） 计算一下摆121根火柴棒时，是第几个图案？
五、（本大题共2小题，每小题10分，满分20分）(共2题；共20分)
19. 如图，一次函数的图象与反比例函数的图象相交于两点，与轴交于点 ．
（1） 求一次函数的解析式；
（2） 设为线段上的一个动点（不包括两点），过点作轴交反比例函数图象于点 ， 当的面积是4时，求点的坐标．
20. 如图，四边形内接于 ， 是的直径，两点关于对称，过点作的切线，交的延长线于点 ．
（1） 求证：；
（2） 若 ， 且 ， 求线段的长．
六、（本题满分12分）(共1题；共12分)
21. 高尔基说：“书，是人类进步的阶梯．”阅读可以启智增慧，拓展视野．为了解学生寒假阅读情况，开学初学校进行了问卷调查，并对部分学生假期（28天）的阅读总时间作了随机抽样分析．设被抽样的每位同学寒假阅读的总时间为 ， 阅读总时间分为四个类别： ， ， ， ， 将分类结果制成两幅统计图（尚不完整）．
根据以上信息，回答下列问题：
（1） 本次抽样的样本容量为 ▲ ， 请补全条形统计图；
（2） 扇形统计图中的值为____________________，圆心角的度数为____________________；
（3） 若该校有2000名学生，估计寒假阅读的总时间少于的学生有多少名？
七、（本题满分12分）(共1题；共12分)
22. 加强劳动教育，落实五育并举．某中学在当地政府的支持下，建成了一处劳动实践基地.2023年计划将其中的土地全部种植甲、乙两种蔬菜．经调查发现：甲种蔬菜种植成本（元）与其种植面积的函数关系如图所示，其中；乙种蔬菜的种植成本为50元 ．
（1） 当____________________时，元；
（2） 设2023年甲、乙两种蔬菜总种植成本为元，如何分配两种蔬菜的种植面积使最小？
（3） 学校计划今后每年在这土地上，均按（2）中方案种植蔬菜，因技术改进，预计种植成本逐年下降．若甲种蔬菜种植成本平均每年下降 ， 乙种蔬菜种植成本平均每年下降 ， 当为何值时，2025年的总种植成本为28920元？
八、（本题满分14分）(共1题；共14分)
23. 如图1，在正方形中，点分别在边上， ， 连接交于点 ．
图1 图2
（1） 求证：；
（2） 如图2，在（1）的条件下，连接 ， 取的中点 ， 连接 ， 求证：；
（3） 在（2）的条件下，若 ， 求的值． A .
B .
C . 0
D . 2
A .
B .
C .
D .
A .
B .
C .
D .
A .
B .
C .
D .
A .
B .
C .
D .
A .
B .
C .
D .
A .
B .
C .
D .
A .
B .
C . 5
D .
A .
B .
C .
D .
A .
B . 或
C .
D . 或