

黑龙江省哈尔滨市萧红中学2023-2024学年八年级下学期月考数学试题
展开1.下列方程中,属于一元二次方程的是( ).
A.B.C.D.
2.以下列各组数为边长,能构成直角三角形的是( )
A.B.C.D.
3.下列各曲线表示的与之间的关系中,不是的函数的是( ).
A.B.C.D.
4.菱形具有而矩形不一定具有的性质是( ).
A.对边相等B.对角线互相垂直C.对角线相等D.对角线互相平分
5.一元二次方程根的情况为( ).
A.有两个不相等的实数根B.有两个相等的实数根
C.无实数根D.有一个实数根
6.下列给出的条件中,不能判定四边形是平行四边形的是( )
A.,B.,
C.,D.,
7.对于一次函数,下列结论错误的是( ).
A.函数值随的增大而减小B.函数图象向下平移5个单位得的图象
C.函数图象与轴的交点是D.当时,
8.如图,长方形中,,,将此长方形折叠,使点与点重合,折痕为,则的面积为( ).
(第8题图)
A.B.C.D.
9.某农机厂四月份生产零件50万个,六月份生产零件182万个.设该厂生产零件平均每月的增长率为,那么满足的方程是( )
A.B.
C.D.
10.某市初中学业水平考试体育学科的女子800米耐力测试中,在某考点同时起跑的小莹和小梅所跑的路程(米)与所用时间(秒)之间的函数图象分别为线段和折线,下列说法正确的是( ).
(第10题图)
A.小莹的速度随时间的增大而增大B.小梅的平均速度比小莹的平均速度大
C.在起跑后180秒时.两人相遇D.在起跑后50秒时.小梅在小莹的前面
二、填空题(每小题3分,共计30分)
11.函数中,自变量的取值范围是______.
12.中,,则______.
13.已知一次函数的图象经过点则______.
14.矩形中,对角线相交于点,,,则______.
15.若关于的一元二次方程有一个根为2,则的值是______.
16.如图,在正方形的外侧,作等边,则______.
(第16题图)
17.某种植物的主干长出若干数目的支干,每个支干又长出同样多数目的小分支,主干、支干、小分支一共是43个,则每个支干长出的小分支数目为______.
18.将直线沿轴平移两个单位长度后得到直线,则直线与轴交点的坐标为______.
19.已知中,,,,则______.
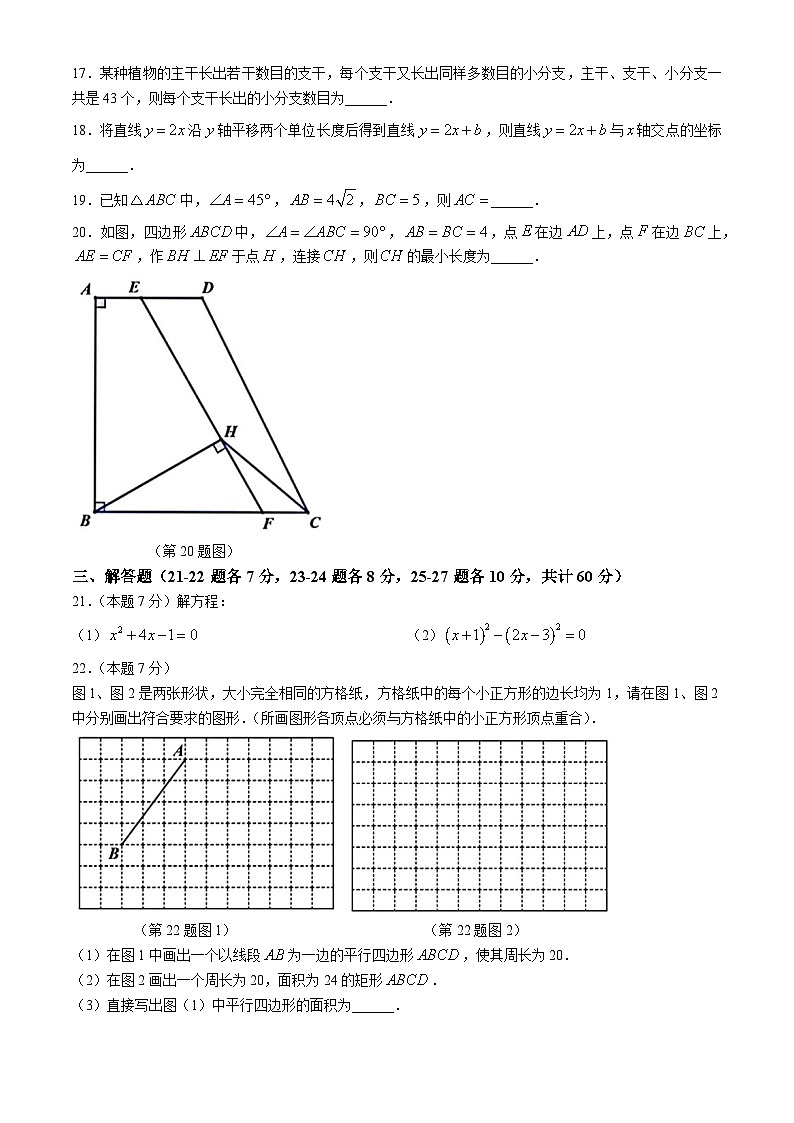
20.如图,四边形中,,,点在边上,点在边上,,作于点,连接,则的最小长度为______.
(第20题图)
三、解答题(21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.(本题7分)解方程:
(1)(2)
22.(本题7分)
图1、图2是两张形状,大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,请在图1、图2中分别画出符合要求的图形.(所画图形各顶点必须与方格纸中的小正方形顶点重合).
(第22题图1) (第22题图2)
(1)在图1中画出一个以线段为一边的平行四边形,使其周长为20.
(2)在图2画出一个周长为20,面积为24的矩形.
(3)直接写出图(1)中平行四边形的面积为______.
23.(本题8分)
如图,在平面直角坐标系中,点为坐标原点,直线分别交轴、轴于点,直线分别交轴、轴于点,直线相交于点,连接.
(第23题图)
(1)直接填空:点坐标(______,0),点C坐标(______,0),点B坐标(0,______),直线的解析式为______;
(2)求点坐标和的面积.
24.(本题8分)在中,于点,点是边的中点,过作,交的延长线于点,连接.
(第24题图1) (第24题图2)
(1)如图1,求证:四边形是矩形;
(2)如图2,当时,取中点,连接,在不添加任何辅助线和字母的情况下,请直接写出图中所有的平行四边形.(不包括矩形和)
25.(本题10分)
百货商店服装柜在销售中知悉:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,以扩大销售量,增加盈利.经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件.
(1)设每套童装降价元,每天的销售量为件,在保证不赔的前提下,求关于的函数关系式,并直接写出自变量的取值范围;
(2)要平均每天销售这种童装盈利1200元,并尽快减少库存,那么每件童装应降价多少元?
26.(本题10分)阅读理解,并回答以下问题:
(1)我们定义,在中,一个锐角所对的直角边和相邻直角边的比叫做这个锐角的“正切”,用符号记作“”.如图1:小正方形方格边长均为1,在中,,则______,在上截取,连接,经“勾股定理”计算______, ,也因此可以把叫做“2倍角三角形”,从中得规律:,并可以在以下习题里直接运用;
(2)如图2:小正方形方格边长均为1,的值为______,在射线上找一点,使得是二倍角三角形,其中,连接,请画出图形,并直接写出______;
(3)如图3:在中,连接,过点作于点,,若,,求的面积.
27.(本题10分)已知,平面直角坐标系中,点为坐标原点,直线交轴于点,交轴于点.
(27题图1) (27题图2) (27题图3)
(1)如图1,求点,点的坐标;
(2)如图2,直线(为常数且)交轴于点,交轴于点,,求的面积关于的函数关系式;
(3)在(2)的条件下,将直线向下平移个单位长度,得到的直线与直线交于点,点在轴上,点在直线上,当为等腰直角三角形时,求点的坐标.
答案
1.D2.B3.C4.B
5.B6.A7.C8.A
9.A10.D
11.12.12013.214.2.5
16.6017.618.或19.1或7
20.
21.(本题7分)
解:(1)
,
(2)
或 ,
(2)解:整理得:,
,,
,
方程有两个不相等的实数根
,
即,
22.(本题7分)
解:略(1)正确画图.
(2)画图正确.
(3)20
23.(本题8分)
(2)解:(1)点A坐标,点C坐标,点B坐标,
直线的解析式为;
(2)作轴于点,
解得:
,
24.(1)先证四边形是平行四边形,再证矩形
(2),,,.
25.解:(1)(也可以体现在列式中,直接用2扣1分)
自变量的取值范围是.
(2)依题意得,
整理,得,
解得,.
因要尽量减少库存,故x应取20.
答:每套应降价20元
26.(1),
(2),
(3)导角:,延长至点,使,连接.
勾股:.,
27.(1)
(2),
(3)
点坐标或或或
黑龙江省哈尔滨市南岗区萧红中学2023-2024学年九年级下学期月考数学试题: 这是一份黑龙江省哈尔滨市南岗区萧红中学2023-2024学年九年级下学期月考数学试题,共27页。试卷主要包含了选择题,四象限,,计算题,解答题等内容,欢迎下载使用。
黑龙江省哈尔滨市萧红中学校2023-2024学年八年级下学期月考数学试题(无答案): 这是一份黑龙江省哈尔滨市萧红中学校2023-2024学年八年级下学期月考数学试题(无答案),共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
黑龙江省哈尔滨市萧红中学校2023-2024学年八年级下学期3月考数学试题: 这是一份黑龙江省哈尔滨市萧红中学校2023-2024学年八年级下学期3月考数学试题,共6页。












