






新教材(广西专版)高考数学一轮复习第九章平面解析几何第一节直线的倾斜角、斜率与直线的方程课件
展开知识梳理1.直线倾斜角的定义定义:当直线l与x轴相交时,我们以x轴为基准,x轴 与直线l______的方向之间所成的角α叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为 .
直线的倾斜角α的取值范围为0°≤α<180°
2.直线的斜率(1)定义:一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即k=tan α,倾斜角是90°的直线斜率不存在.(2)过两点的直线的斜率公式
经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为
所有的直线都有倾斜角,但不是所有的直线都有斜率
微点拨斜率公式与两点的顺序无关,即两纵坐标和两横坐标在公式中可以同时调换.就是说,如果分子是y2-y1,那么分母必须是x2-x1;反过来,如果分子是y1-y2,那么分母必须是x1-x2.
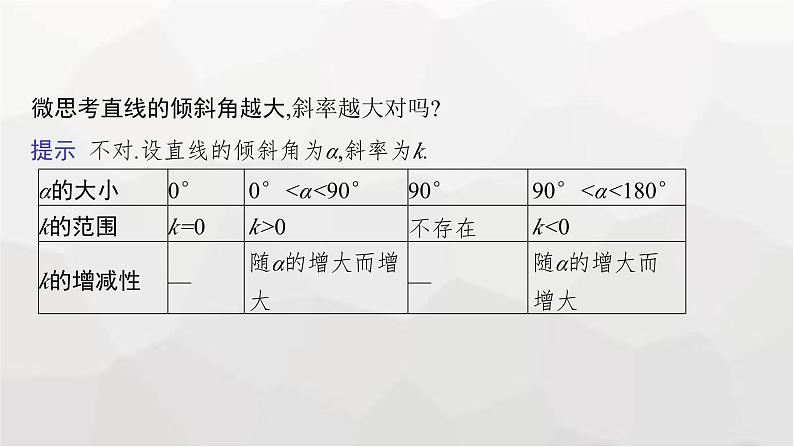
微思考直线的倾斜角越大,斜率越大对吗?
提示 不对.设直线的倾斜角为α,斜率为k.
3.直线方程的五种形式
“截距式”中的截距不是距离,在用截距式时,应先判断截距是否为0
y-y0=k(x-x0)
微点拨求直线方程时,若不能判断直线是否具有斜率,应对斜率“存在”与“不存在”加以讨论.
常用结论1.直线的倾斜角α和斜率k之间的对应关系
2.特殊位置的直线方程(1)与x轴重合的直线方程为y=0;(2)与y轴重合的直线方程为x=0;(3)过点(a,b)(b≠0)且平行于x轴的直线方程为y=b(b≠0);(4)过点(a,b)(a≠0)且平行于y轴的直线方程为x=a(a≠0);(5)过原点且斜率为k的直线方程为y=kx.
对点演练1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)过点M(a,b),N(b,a)(a≠b)的直线的倾斜角是45°.( )(2)若直线的斜率为tan α,则其倾斜角为α.( )(3)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示.( )(4)直线的截距即直线与坐标轴的交点到原点的距离.( )
2.若过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为( )A.1B.4C.1或3D.1或4
解析 因为过点M(-2,m),N(m,4)的直线的斜率等于1,所以k= =1,解得m=1.故选A.
3.(多选)下列说法正确的是( )A.有的直线斜率不存在B.若直线l的倾斜角为α,且α≠90°,则它的斜率k=tan αC.若直线l的斜率为1,则它的倾斜角为D.截距可以为负值
解析 选项A中,倾斜角为90°的直线的斜率不存在,故A正确;选项B中,根据斜率的定义可得B正确;选项C中,当倾斜角θ= 时,tan θ=1,当倾斜角θ= 时,tan θ=-1,故C错误;选项D中,截距可以为正,也可以为负,还可以为0,故D正确.故选ABD.
典例突破例1.(1)若图中的直线l1,l2,l3的斜率分别是k1,k2,k3,则有( )A.k1
(3)(多选)(2023黑龙江哈尔滨三中二模)点M(x1,y1)在函数y=ex的图象上,若x1∈[0,1),则 可能等于( )A.-1B.-2C.-3D.0
答案 (1)D (2)C (3)BC
解析 (1)由题图可知k1>0,k2<0,k3<0,且直线l3的倾斜角大于直线l2的倾斜角,所以k3>k2.综上可知k2
名师点析求倾斜角的取值范围的一般步骤
对点训练1(1)(多选)若直线l1:ax-y-b=0,l2:bx-y+a=0,ab≠0,a≠b,则下列图形可能正确的是( )
(3)(2023湖南株洲一模)过原点的直线l与曲线y=ex-1交于不同的两点A,B,过A,B作x轴的垂线,与曲线y=ln x交于C,D两点,则直线CD的斜率为 .
解析 (1)直线l1:ax-y-b=0可化为y=ax-b,直线l2:bx-y+a=0可化为y=bx+a.对于选项A,由l1得a>0,b<0,由l2得b<0,a>0,故A正确;对于选项B,由l1得a>0,b>0,由l2得b>0,a>0,故B正确;对于选项C,由l1得a<0,b<0,由l2得b>0,a>0,故C不正确;对于选项D,由l1得a<0,b<0,由l2得b<0,a>0,故D不正确.故选AB.
(2)设切线倾斜角为α,∵y'=x2-2x=(x-1)2-1≥-1,∴切线的斜率k=tan α≥-1,
典例突破例2.写出下列直线的方程:
(2)直线过点(-3,4),且在两坐标轴上的截距之和为12;(3)直线过点(5,10),且到原点的距离为5.
(3)当斜率不存在时,所求直线方程为x-5=0,满足题意.当斜率存在时,设斜率为k,则所求直线方程为y-10=k(x-5),即kx-y+10-5k=0.由点到直线的距离公
方法总结求直线方程的两种方法
对点训练2(1)在等腰三角形MON中,|MO|=|MN|,点O(0,0),M(-1,3),点N在x轴的负半轴上,则直线MN的方程为( )A.3x-y-6=0B.3x+y+6=0C.3x-y+6=0D.3x+y-6=0
(2)(多选)已知直线l过点(3,4),点A(-2,2),B(4,-2)到l的距离相等,则l的方程可能是( )A.x-2y+2=0B.2x-y-2=0C.2x+3y-18=0D.2x-3y+6=0
(3)过点P(6,-2),且在x轴上的截距比在y轴上的截距大1的直线方程为 .
答案 (1)C (2) BC (3)2x+3y-6=0或x+2y-2=0
解析 (1)因为|MO|=|MN|,点N在x轴的负半轴上,所以直线MN的斜率与直线MO的斜率互为相反数,所以kMN=-kMO=3,所以直线MN的方程为y-3=3(x+1),即3x-y+6=0.故选C.
考向1.直线过定点问题典例突破例3.(1)直线ax+(a+1)y+a-1=0过定点( )A.(2,1)B.(2,-3)C.(-2,1)D.(-2,3)(2)已知实数m,n满足2m-n=1,则直线mx-3y+n=0必过定点 .
名师点析1.直线过定点问题,可以根据方程的结构特征,得出直线过定点的坐标.2.含有参数的直线方程可看作直线系方程,这时要能够整理成过定点的直线系,即能够看出“动中有定”.
对点训练3(1)对于任意的实数k,直线y=kx-k+1恒过定点P,则点P的坐标为( )A.(-1,-1)B.(-1,1)C.(1,-1) D.(1,1)
(2)(2023吉林东北师大附中二模)直线l的方程为(λ+2)x+(λ-1)y-3λ=0(λ∈R),当原点O到直线l的距离最大时,λ的值为( )A.-1B.-5C.1D.5
答案 (1)D (2) B
解析 (1)由y=kx-k+1可得y-1=k(x-1),所以直线y=kx-k+1恒过定点P(1,1).故选D.
考向2.与直线方程有关的最值问题典例突破例4.过点P(4,1)作直线l分别交x轴、y轴的正半轴于A,B两点,点O为坐标原点.(1)当△AOB面积最小时,求直线l的方程;(2)当|OA|+|OB|取最小值时,求直线l的方程.
方法总结与直线方程有关的最值问题的解题策略
对点训练4(1)(2023北京海淀模拟)已知直线l:ax+by=1.若l上有且仅有一点P,使得以点P为圆心,1为半径的圆过原点O,则a-b的最大值为( )
C.2 D.1(2)已知直线l1:ax-2y=2a-4,l2:2x+a2y=2a2+4.当0
2025届高考数学一轮总复习第九章平面解析几何第一节直线的倾斜角斜率与直线的方程课件: 这是一份2025届高考数学一轮总复习第九章平面解析几何第一节直线的倾斜角斜率与直线的方程课件,共42页。PPT课件主要包含了强基础增分策略,答案A,答案ABD,增素能精准突破等内容,欢迎下载使用。
2025版高考数学一轮总复习第8章平面解析几何第1讲直线的倾斜角斜率与直线的方程课件: 这是一份2025版高考数学一轮总复习第8章平面解析几何第1讲直线的倾斜角斜率与直线的方程课件,共60页。PPT课件主要包含了考情探究,0°180°,正切值,tanα,y=kx+b,两点式,截距式,过原点的,A2+B2≠0,题组二走进教材等内容,欢迎下载使用。
适用于新教材2024版高考数学一轮总复习第九章平面解析几何第一节直线的倾斜角斜率与直线的方程课件北师大版: 这是一份适用于新教材2024版高考数学一轮总复习第九章平面解析几何第一节直线的倾斜角斜率与直线的方程课件北师大版,共34页。PPT课件主要包含了内容索引,强基础固本增分,研考点精准突破,直线的斜率,答案C等内容,欢迎下载使用。












