广东省深圳市2024年中考三模数学试卷（解析版）

这是一份广东省深圳市2024年中考三模数学试卷（解析版），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题，满分30分，每小题3分）
1. 北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一，具有极高的历史价值、文化价值．如图所示，关于它的从正面、左面、上面三个不同的方向观察看到的平面图形，下列说法正确的是（ ）
A. 从正面看与从左面看到的图形相同B. 从正面看与从上面看到的图形相同
C. 从左面看与从上面看到的图形相同D. 从正面、左面、上面看到的图形都相同
【答案】A
【解析】由题意可知，该几何体从正面和左面看到的形状图相同．
故选：A．
2. 若关于的一元二次方程的一个根是，则的值是（ ）
A. B. C. 3D. 6
【答案】D
【解析】将代入，得：，
解得，
故选D．
3. 如图，在菱形中，．已知的周长是15，则菱形的周长是（ ）
A. 23B. 20C. 15D. 10
【答案】B
【解析】四边形是菱形，是对角线，
，，
，
是等边三角形，
∵的周长是15，
，
菱形的周长是20
故选：B．
4. 将方程化成（m、n为常数）的形式，则m、n的值分别为（ ）
A. B.
C. D.
【答案】A
【解析】，
，
，
，
，
故选：A．
5. 近几年，二维码逐渐进入了人们的生活，成为广大民众生活中不可或缺的一部分．小刚将二维码打印在面积为20的正方形纸片上，如图，为了估计黑色阴影部分的面积，他在纸内随机掷点，经过大量实验，发现点落在黑色阴影的频率稳定在左右，则据此估计此二维码中黑色阴影的面积为（ ）
A. 8B. 12C. 0.4D. 0.6
【答案】B
【解析】∵经过大量实验，发现点落在黑色阴影的频率稳定在左右，
∴点落在阴影部分的概率为，
设阴影部分面积为S，则，
即：，
∴黑色阴影的面积为12，
故选：B．
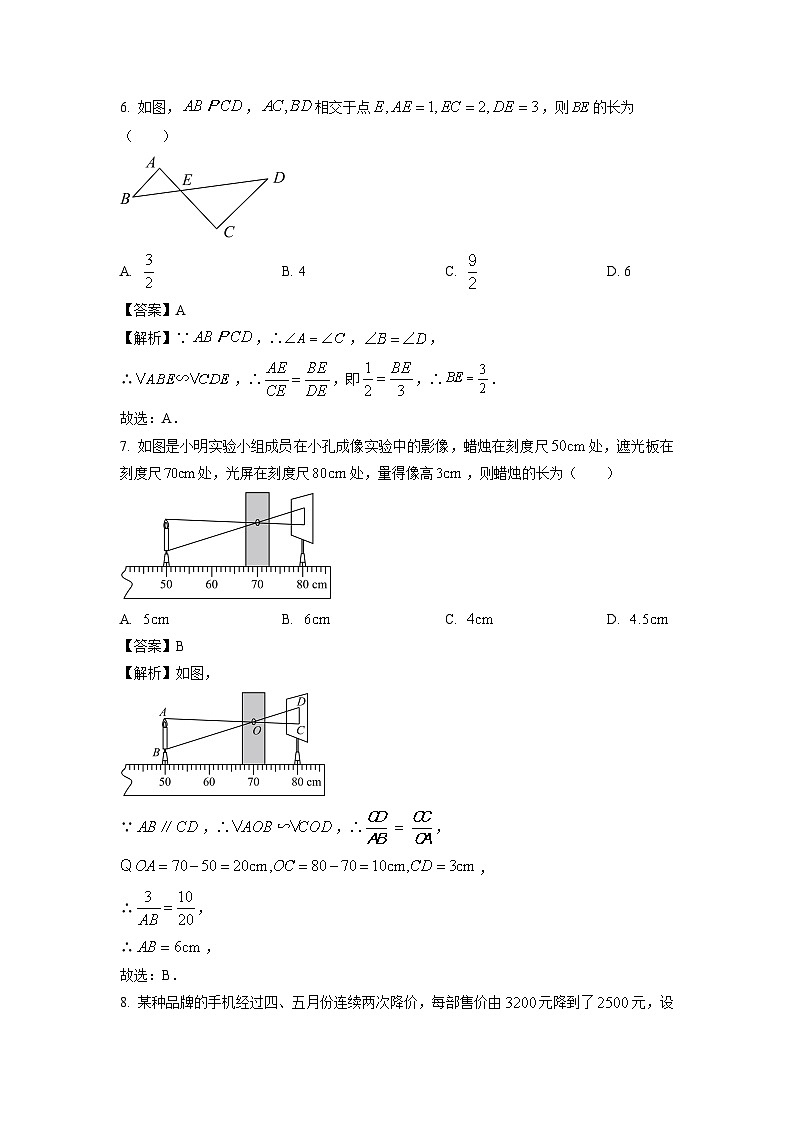
6. 如图，，相交于点，则的长为（ ）

A. B. 4C. D. 6
【答案】A
【解析】∵，∴，，
∴，∴，即，∴．
故选：A．
7. 如图是小明实验小组成员在小孔成像实验中的影像，蜡烛在刻度尺处，遮光板在刻度尺处，光屏在刻度尺处，量得像高，则蜡烛的长为（ ）
A. B. C. D.
【答案】B
【解析】如图，
∵，∴，∴，
，
∴，
∴，
故选：B．
8. 某种品牌的手机经过四、五月份连续两次降价，每部售价由元降到了元，设平均每月降低的百分率为x，根据题意列出的方程是（ ）
A. B.
C. D.
【答案】D
【解析】设平均每月降低的百分率为x，
依题意得：，
故选：D.
9. 喜迎二十大，“龙舟故里”赛龙舟，小亮在龙舟竞渡中心广场点P处观看400米直道竞速赛，如图所示，赛道AB为东西方向，赛道起点A位于点P的北偏西方向上，终点B位于点P的北偏东方向上，米，求点P到赛道AB的距离（ ）（结果保留整数，参考数据：）
A B. C. 87D. 173
【答案】D
【解析】过点P作，垂足为C，
设米，
在中，，
∴（米），
在中，，
∴（米），
∵米，
∴，
∴，
∴，
∴米，
∴点P到赛道的距离约为173米，
故选D．
10. 如图，CB＝CA，∠ACB＝90°，点D在边BC上(与B，C不重合)，四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC＝FG；②S△FAB∶S四边形CBFG＝1∶2；③∠ABC＝∠ABF；④AD2＝FQ·AC，其中正确结论的个数是( )
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】∵四边形ADEF正方形，∴∠FAD=90°，AD=AF=EF，
∴∠CAD+∠FAG=90°，
∵FG⊥CA，∴∠GAF+∠AFG=90°，∴∠CAD=∠AFG，
在△FGA和△ACD中，，
∴△FGA≌△ACD（AAS），∴AC=FG，①正确；
∵BC=AC，∴FG=BC，
∵∠ACB=90°，FG⊥CA，∴FG∥BC，∴四边形CBFG是矩形，
∴∠CBF=90°，S△FAB=FB•FG=S四边形CBFG，②正确；
∵CA=CB，∠C=∠CBF=90°，
∴∠ABC=∠ABF=45°，③正确；
∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，
∴△ACD∽△FEQ，
∴AC：AD=FE：FQ，
∴AD•FE=AD2=FQ•AC，④正确；
故选D．
第二部分 非选择题
二、填空题（共5小题，满分15分，每小题3分）
11. 若，则________．
【答案】
【解析】，，
故答案为：．
12. 2011年3月11日13∶46日本发生了震惊世界的大地震，近期国际机构将日本核电事故等级上调至国际核能事件分级表（INES）中最严重的7级，据估算其向大气排放的放射性物质量约为630000太贝克，数据630000用科学记数法表示为：______．
【答案】
【解析】数据630000用科学记数法表示：．
故答案为：．
13. 五一期间，小明和小亮分别从四部影片《飞驰人生2》、《热辣滚烫》、《九龙城寨之围城》、《维和防暴队》中随机选择一部观看，则他们选择的影片相同的概率为______．
【答案】
【解析】分别记《飞驰人生2》、《热辣滚烫》、《九龙城寨之围城》、《维和防暴队》为
列表如下：
他们选择的影片相同的概率为：
故答案为：．
14. 如图，在平面直角坐标系中，直线与轴交于点A（-4，0），与轴夹角为，将沿直线翻折，点的对应点恰好落在双曲线上，则的值为______．
【答案】
【解析】设点的坐标为，如图，过点作轴，作轴，
将沿直线翻折，
，，，
∴∠CAD=60°， ∠ACD=30°，
，
，
，
，
，
点在第二象限，
，
点恰好落在双曲线上，
．
故答案为：．
15. 如图，OA在 x轴上，OB在y轴上，OA=8，AB=10，点C在边OA上，AC=2，P的圆心P 在线段BC上，且P与边AB，AO都相切．若反比例函数（k≠0）的图象经过圆心P，则k=________________．
【答案】-5
【解析】方法1：作PD⊥OA于D，PE⊥AB于E，作CH⊥AB于H，如图，设⊙P的半径为r，
∵⊙P与边AB，AO都相切，∴PD=PE=r，AD=AE，在Rt△OAB中，
∵OA=8，AB=10，∴OB==6，
∵AC=2，∴OC=6，∴△OBC为等腰直角三角形，
∴△PCD为等腰直角三角形，∴PD=CD=r，∴AE=AD=2+r，
∵∠CAH=∠BAO，∴△ACH∽△ABO，
∴，即，解得CH=，
∴AH===，∴BH==，
∵PE∥CH，∴△BEP∽△BHC，
∴，即，解得r=1，
∴OD=OC﹣CD=6﹣1=5，∴P（5，﹣1），∴k=5×（﹣1）=﹣5．故答案为﹣5．
方法2 由，，，
可得，故．即点P的纵坐标为-1，又因为点P在直线BC：上，所以点P的横坐标为5，故．
方法3 注意到AP平分，也可利用角平分线性质求解．由，可设，．
于是，可得．
又因为，所以．
三、解答题（共7小题，满分55分）
16. 解方程：．
解：∵，
∴，
∴或，
解得．
17. 班级开展迎新年联欢晚会时，在教室悬挂了如图所示的四个福袋A，B，C，D．在抽奖时，每次随机取下一个福袋，且取A之前需先取下，取之前需先取下，直到4个福袋都被取下．
（1）第一个取下的是福袋的概率为_______．
（2）请用画树状图或列表的方法，求第二个取下的是A福袋的概率．
解：（1）∵第一次摘只能先从和中选择任意一个，
∴第一个摘下灯笼的概率是．
故答案为：．
（2）根据题意画出状态如下：
由树状图可得：所有等可能情况有4种，其中第二个取下的是A福袋的情况有1种，
第二个取下的是A福袋的概率为．
18. 家庭过期药品属于“国家危险废物“处理不当将污染环境，危害健康．某市药监部门为了了解市民家庭处理过期药品的方式，决定对全市家庭作一次简单随机抽样调查本次抽样调查发现，接受调查的家庭都有过期药品，现将有关数据呈现如图：
（1）求m、n的值；
（2）补全条形统计图；
（3）家庭过期药品的正确处理方式是送回收站，若该市有180万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收站．
解：（1）∵抽样调查的家庭总户数为：80÷8%=1000（户），
∴m%==20%，m=20，
n%==6%，n=6．
（2）C类户数为：1000﹣（80+510+200+60+50）=100，
条形统计图补充如下：
（3）180×10%=18（万户）．
若该市有180万户家庭，估计大约有18万户家庭处理过期药品的方式是送回收点．
19. 山清水秀的东至县三条岭已成为游客最喜欢的旅游地之一，其中“蔡岭”在2019年“五一”小长假期间，接待游客达2万人次，预计在2021年“五一”小长假期间，接待游客2.88万人次，在蔡岭，一家特色小面店希望在“五一”小长假期间获得好的收益，经测算知，该小面成本价为每碗10元，借鉴以往经验，若每碗卖15元，平均每天将销售120碗，若价格每提高0.5元，则平均每天少销售4碗，每天店面所需其他各种费用为168元．
（1）求出2019至2021年“五一”小长假期间游客人次的年平均增长率；
（2）为了更好地维护东至县形象，物价局规定每碗售价不得超过20元，则当每碗售价定为多少元时，店家才能实现每天净利润600元？（净利润＝总收入﹣总成本﹣其它各种费用）
解：（1）可设年平均增长率为x，依题意，得：2（1＋x）2＝2.88，
解得：x1＝0.2＝20%，x2＝﹣2.2（舍去）．
答：年平均增长率为20%；
（2）设每碗售价定为y元时，店家才能实现每天利润600元，依题意得：
（y﹣10）·[120﹣（y﹣15）]﹣168＝600，
解得：y1＝18，y2＝22，
∵每碗售价不得超过20元，
∴y＝18．
答：当每碗售价定为18元时，店家才能实现每天利润600元．
20. 如图，点E是矩形对角线上的点（不与A，C重合），连接，过点E作交于点F．连接交于点．
（1）求证：；
（2）试判断线段与的位置关系，并说明理由．
（1）证明：∵四边形是矩形，
∴，，
∵，
∴，
∴，
∵，
∴，
∴；
（2）解：垂直；
理由：∵，
∴，
∴点F在线段的垂直平分线上．
又∵，
∴点B在线段的垂直平分线上．
∴垂直平分，
∴垂直．
21. （1）【建立模型】在数学课上，老师出示这样一个问题：如图1，在中，，，直线l经过点C，，，垂足分别为点D和点E，求证：，请你写出证明过程；
（2）【类比迁移】勤奋小组在这个模型的基础上，继续进行探究问题：如图2，在平面直角坐标系中，直线的图象与y轴交于点A，与x轴交于点C，将线段绕点C顺时针旋转得到线段，反比例函数的图象经过点B，请你求出反比例函数的解析式；
（3）【拓展延伸】创新小组受到勤奋小组的启发，结合抛物线的图象继续深入探究：如图3，一次函数的图象与y轴交于点A，与x轴交于点C，创新小组的同学发现在第一象限的抛物线的图象上存在一点P，连接，当时，请你和创新小组的同学一起求出点P的坐标．
（1）证明：∵，∴，
∵，∴，∴，
∵，，∴
（2）解：∵，
∴当时，，当时，，，∴，，
由（1）可知：，
∴，，∴，点B的坐标为
把代入得：，解得，
∴反比例函数的解析式为：.
（3）过点C作，且，过点B作轴，垂足为点E，连接交抛物线于点P，
∴，
由（2）可知，，
∴设直线的解析式为，
∴，∴，∴，∴，
解得：，（不合题意，舍去）
当时，，∴.
22. 如图①，点D为上方一动点，且．
（1）在左侧构造，连接，请证明；
（2）如图②，在左侧构造，在右侧构造，连接求证：四边形是平行四边形；
（3）如图③，当满足，，．运用（2）中的构造图形的方法画出四边形；
（Ⅰ）求证：四边形是矩形；
（Ⅱ）直接写出在点D运动过程中线段的最大值．
（1）解：∵，
∴，，
∴，
∴，
（2）证明：由（1）
∵，∴，，∴，
由（1）同理可得，∴，
∵，∴，∴，
∴，
∴四边形是平行四边形；
（3）解：（Ⅰ）由（1）（2）可得，
∴，∵四边形是平行四边形，
∴四边形是矩形.
（Ⅱ），理由如下：
由（Ⅰ）得，作的外接圆，圆心为O，
∵，
∴，
∴圆心O为定点，且半径，
∴，求得，
∴，
∴，，∴，∴，
∴，，∴，
∴.