2024年山东省淄博市临淄区中考二模数学试题（学生版+教师版 ）

这是一份2024年山东省淄博市临淄区中考二模数学试题（学生版+教师版 ），文件包含2024年山东省淄博市临淄区中考二模数学试题教师版docx、2024年山东省淄博市临淄区中考二模数学试题学生版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
注意事项：
1．答题前，考生务必用0.5毫米黑色签字笔将学校、班级、姓名、考试号、座号填写在答题卡和试卷规定位置．
2．选择题每小题选出答案后，用2B铅笔涂黑答题卡对应题目的答案标号；如需改动，用橡皮擦干净后，再选涂其他答案标号．
3．非选择题必须用0.5毫米黑色签字笔作答，字体工整、笔迹清晰，写在答题卡各题目指定区域内；如需改动，先划掉原来答案，然后再写上新答案．严禁使用涂改液、胶带纸、修正带修改．
4．保证答题卡清洁、完整，严禁折叠，严禁在答题卡上做任何标记．
5，评分以答题卡上的答案为依据．不按以上要求作答的答案无效．
一、选择题（本题共10小题，在每小题所给出的四个选项中，只有一个是正确的，每小题4分，满分40分，错选、不选、多选，均记0分．）
1. 的计算结果是（ ）
A. B. C. D.
2. 下列运算正确的是（ ）
A. B.
C. D.
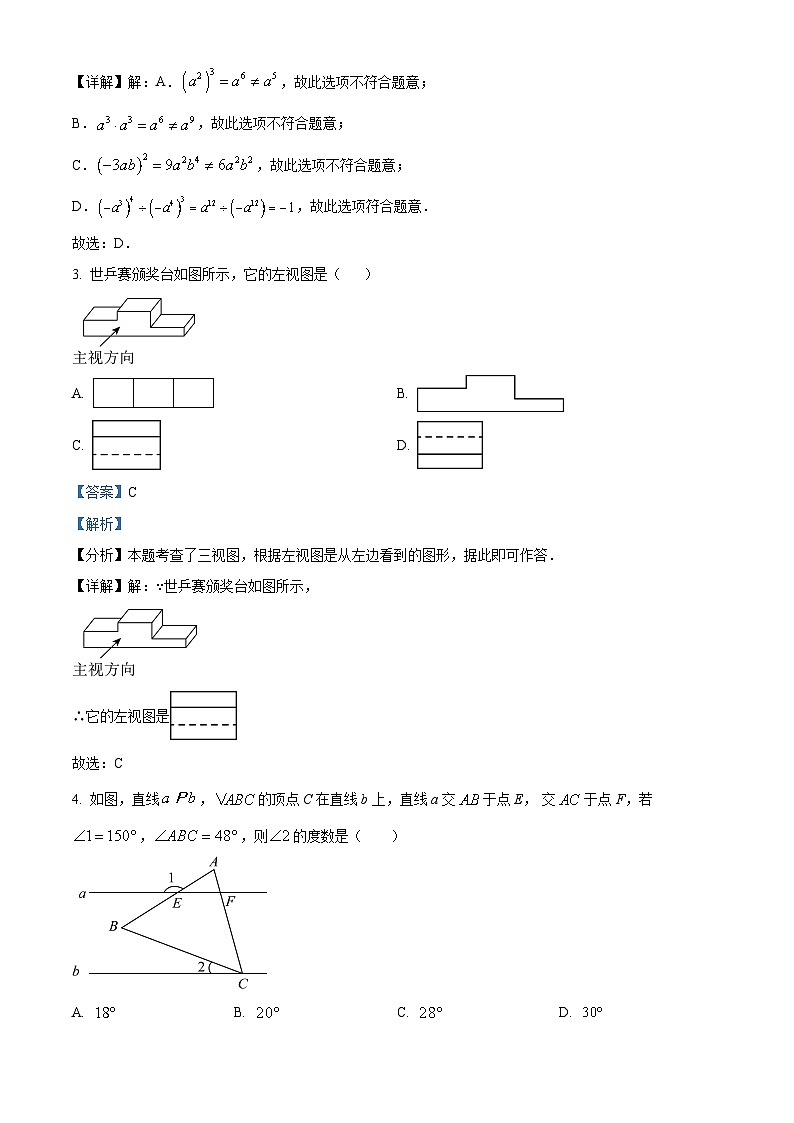
3. 世乒赛颁奖台如图所示，它的左视图是（ ）
A. B.
C D.
4. 如图，直线，的顶点C在直线b上，直线a交于点E， 交于点F，若，，则的度数是（ ）
A. B. C. D.
5. 小亮在网上销售笔记本．最近一周，每天销售某种笔记本的本数为：12，13，14，15，14，16，21．关于这组数据，小亮得出如下结果，其中错误的是（ ）
A. 众数是14本B. 平均数是15本C. 方差是4D. 中位数是14本
6. 若m，n是一元二次方程的两个根，则的值是（ ）
A. B. C. D. 6
7. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式，即三角形的三边长分别为a，b，c，那么面积．若某个三角形的三边长分别为2，3，3，其面积S介于整数和n之间，则n的值为（ ）
A. 2B. 3C. 4D. 5
8. 如图，在平面直角坐标系中，矩形边，分别在x轴，y轴上，点E在边上，将该矩形沿折叠，点B恰好落在边上的F处．若，，则点E的坐标是（ ）
A. B. C. D.
9. 如图，三次函数图象与轴有个交点，分别是，请同学们根据所学过的函数知识进行判断当时，；当时，有最小值；若点在函数的图象上，则的取值只有一个；将函数的图象向左平移个或个单位长度，函数图象经过原点．其中正确的结论有（ ）
A. 个B. 个C. 个D. 个
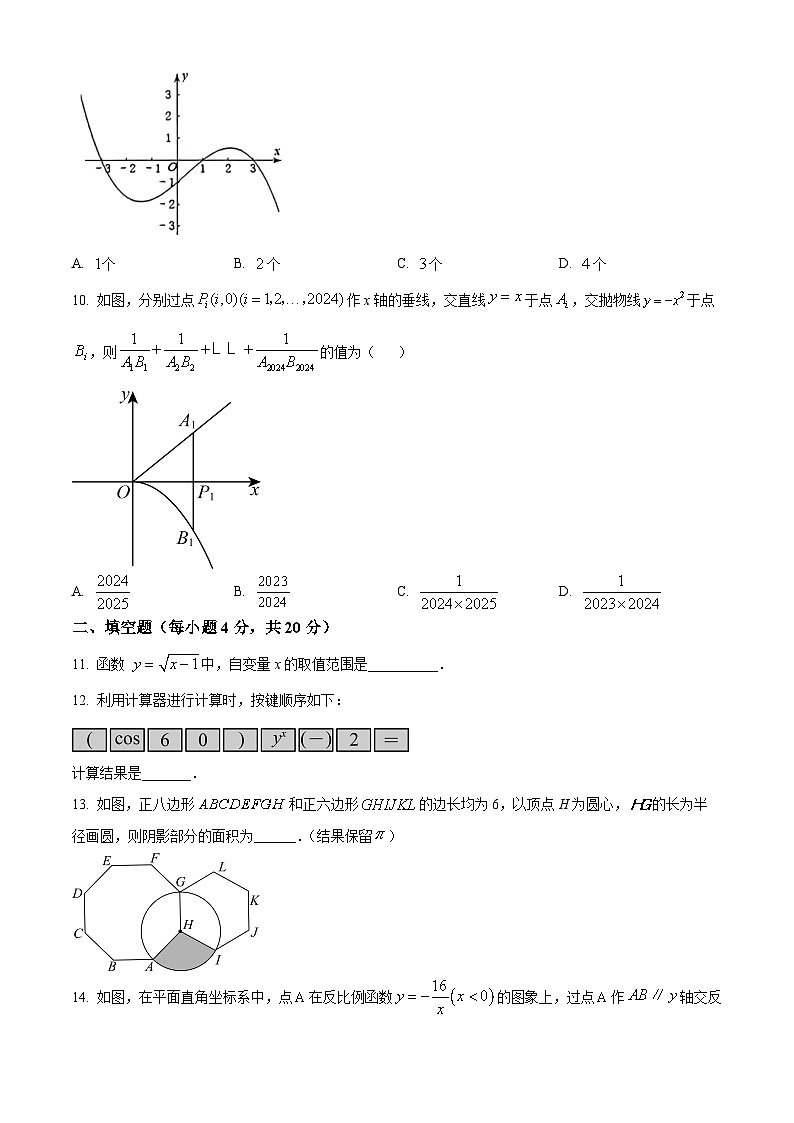
10. 如图，分别过点作x轴的垂线，交直线于点，交抛物线于点，则的值为（ ）
A. B. C. D.
二、填空题（每小题4分，共20分）
11. 函数 中，自变量x的取值范围是__________．
12. 利用计算器进行计算时，按键顺序如下：
计算结果是_______．
13. 如图，正八边形和正六边形的边长均为6，以顶点H为圆心，的长为半径画圆，则阴影部分的面积为______．（结果保留）
14. 如图，在平面直角坐标系中，点在反比例函数的图象上，过点作轴交反比例函数的图象于点，点为轴上一点，连接、，若的面积为，则的值为_______．
15. 如图，在中，，是以斜边为直径的半圆上一动点，为上一点且满足，连接，则的最小值为___________．
三、解答题（第16，17，18，19题每题10分；第20，21题每题12分，第22，23题每题13分；满分90分）解答要写出必要的文字说明、证明过程或演算步骤．
16. （1）计算：
（2）化简，并在，，，中选一个合适的数求值．
17. 如图，在中，于点，于点，与、分别交于点，．
（1）求证：
（2）若，求证四边形是菱形
18. 如图，某座山的项部有一座通讯塔，且点A，B，C在同一条直线上，从地面P处测得塔顶C的仰角为，测得塔底B的仰角为．已知通讯塔的高度为，求这座山的高度（结果取整数）．参考数据：．
19. 为了解甲、乙两个茶园种植的“龙井”茶叶的品质，现从两个茶园里分别随机抽取了20份茶叶样本，对它们的品质进行评分（满分100分，分数越高代表品质越好）．评分用x表示，共分为四组，A组：，B组：，C组：，D组：．
甲茶园20份茶叶的评分从小到大分别为：65，68，72，75，78，80，82，85，85，88，90，90，90，92，95，95，95，95，98，100；
乙茶园20份茶叶中有3份的评分为100分，评分在C组中的数据是：85，88，80，85，82，83．
甲、乙两茶园随机抽取的茶叶评分数据统计分析如下表所示，乙茶园抽取的茶叶评分扇形统计图如图所示：

根据以上信息解答下列问题：
（1）直接写出统计表中a，b的值；
（2）若甲、乙两茶园的茶叶总共有2400份，请估计甲、乙两茶园评分在D组的茶叶共有多少份；
（3）本次抽取的40份茶叶样本中，评分为100分的视为“精品茶叶”．茶农要在“精品茶叶”中任选两份参加茶叶展销会，用列表法（或画树状图）求这两份茶叶全部来自乙茶园的概率．
20. 如图，一次函数的图象与反比例函数的图象交于．
（1）求m，n的值及反比例函数的表达式；
（2）将直线向下平移t个单位，若平移后的直线与反比例函数的图象有唯一交点，求t的值．
21. 【项目式学习】：根据以下素材，探索完成任务．
22. 已知，内接于，平分交边于点E，连接．
（1）如图1，过点D作直线，求证：是的切线：
（2）小明同学围绕圆内接三角形进行了一系列的探究，发现线段之间存在着一种数量关系；
【发现猜想】在图1中，小明同学发现，当时，线段之间满足数量关系
【推理证明】延长AC到点P使得
平分
又
为正三角形
【类比探究】如图2，当时，试猜想线段之间满足数量关系，并证明你的结论；
【一般归纳】如图3，当时，试猜想线段之间满足的数量关系（用含有的三角函数表示），并证明你的结论；
【拓展应用】如图4，过点E作，垂足为G，过点E作，垂足为H，求证：．
23. 如图1所示，直线与轴交于点，与轴交于点，抛物线经过点，．

（1）求抛物线的解析式；
（2）点在抛物线的对称轴上，求的最小值；
（3）如图所示，是线段上的一个动点，过点作垂直于轴的直线与直线和抛物线分别交于点，
①若以，，为顶点的三角形与相似，求的面积；
②若点恰好是线段中点，点是直线上一个动点，在坐标平面内是否存在点，使以点，，，为顶点的四边形是菱形？若存在，请直接写出点的坐标；若不存在，请说明理由．
甲茶园
乙茶园
平均数
中位数
89
b
众数
a
95
奶茶销售
方案制定
问题
素材1
当下很多同学喜欢喝奶茶，在入夏之际深圳某知名奶茶品牌店推出两款爆款水果茶“满杯杨梅”和“芝士杨梅”．每杯“芝士杨梅”的售价比“满杯杨梅”贵2元，购买1杯“芝士杨梅”和2杯“满杯杨梅”共需53元．
素材2
4月27日恰逢周末，该奶茶店生意比平时好，当天销售“芝士杨梅”共获利润400元，“满杯杨梅”获利润480元，其中每杯“芝士杨梅”的利润是每杯“满杯杨梅”的倍，“满杯杨梅”比“芝士杨梅”多卖20杯．
问题解决
任务1
确定奶茶的售价
每杯“芝士杨梅”和“满杯杨梅”的售价是多少？
任务2
确定奶茶的成本
每杯“芝士杨梅”和“满杯杨梅”的成本是多少？（每杯利润=每杯售价－每杯成本=）