2024北京中考名校密题：数学最后冲刺30题-函数-函数基础

这是一份2024北京中考名校密题：数学最后冲刺30题-函数-函数基础，共18页。试卷主要包含了 下面的三个问题中都有两个变量，800要求清洗后的清洁度为0等内容，欢迎下载使用。


1. 下面的三个问题中都有两个变量：
①汽车从A地匀速行驶到B地，汽车的剩余路程y与行驶时间x；
②将水箱中的水匀速放出，直至放完，水箱中的剩余水量y与放水时间x；
③用长度一定的绳子围成一个矩形，矩形的面积y与一边长x，其中，变量y与变量x之间的函数关系可以利用如图所示的图象表示的是（ ）
2. 某小组研究了清洗某种含污物品的节约用水策略．部分内容如下．
每次清洗1个单位质量的该种含污物品，清洗前的清洁度均为0.800要求清洗后的清洁度为0.990
方案一：采用一次清洗的方式．
结果：当用水量为19个单位质量时，清洗后测得的清洁度为0.990．
方案二：采用两次清洗的方式．
记第一次用水量为个单位质量，第二次用水量为个单位质量，总用水量为个单位质量，两次清洗后测得的清洁度为C．记录的部分实验数据如下：
对以上实验数据进行分析，补充完成以下内容．
（Ⅰ）选出C是0.990的所有数据组，并划“√”；
（Ⅱ）通过分析（Ⅰ）中选出的数据，发现可以用函数刻画第一次用水量和总用水量之间的关系，在平面直角坐标系中画出此函数的图象；

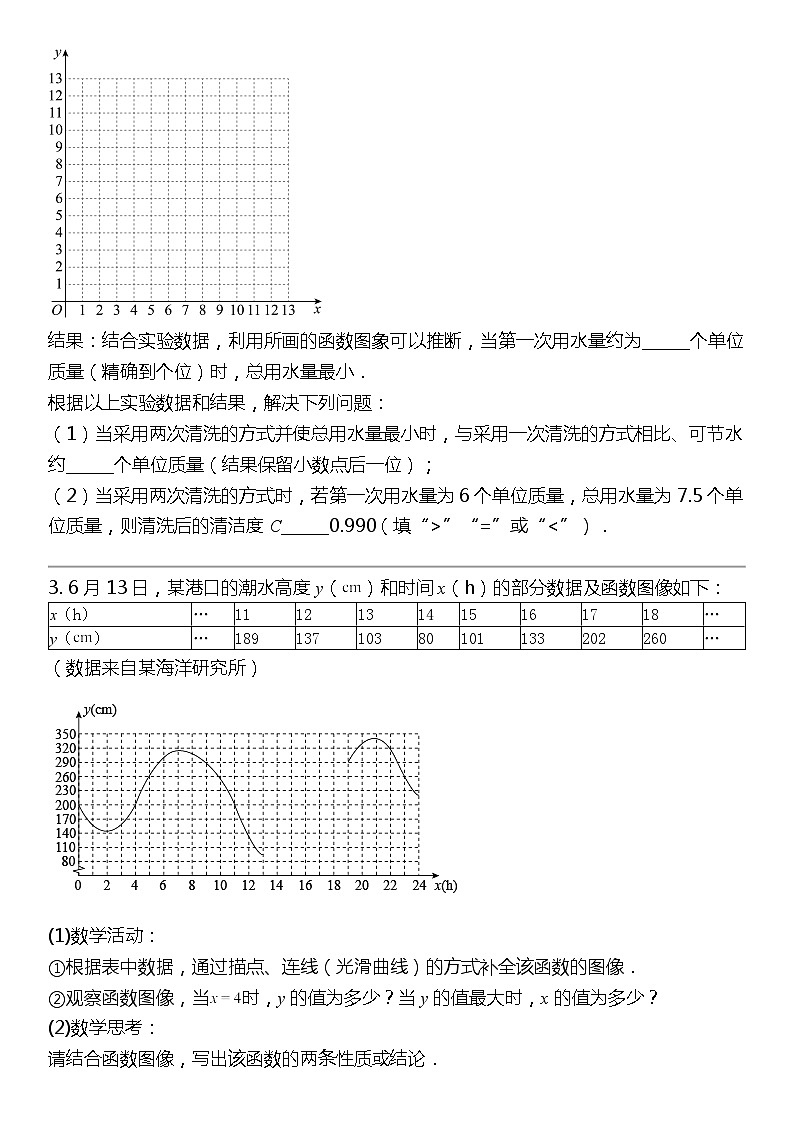
结果：结合实验数据，利用所画的函数图象可以推断，当第一次用水量约为______个单位质量（精确到个位）时，总用水量最小．
根据以上实验数据和结果，解决下列问题：
（1）当采用两次清洗的方式并使总用水量最小时，与采用一次清洗的方式相比、可节水约______个单位质量（结果保留小数点后一位）；
（2）当采用两次清洗的方式时，若第一次用水量为6个单位质量，总用水量为7.5个单位质量，则清洗后的清洁度C______0.990（填“>”“=”或“<”）．
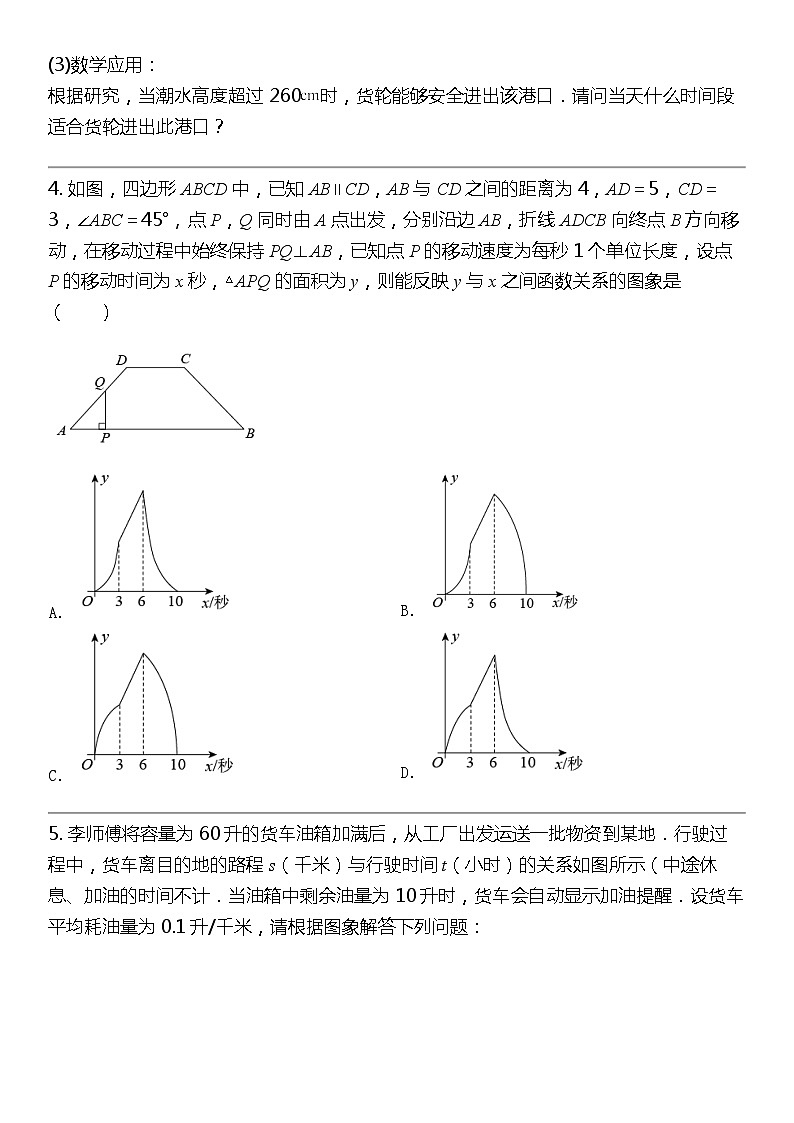
3. 6月13日，某港口的潮水高度y（）和时间x（h）的部分数据及函数图像如下：
（数据来自某海洋研究所）
(1)数学活动：
①根据表中数据，通过描点、连线（光滑曲线）的方式补全该函数的图像．
②观察函数图像，当时，y的值为多少？当y的值最大时，x的值为多少？
(2)数学思考：
请结合函数图像，写出该函数的两条性质或结论．
(3)数学应用：
根据研究，当潮水高度超过260时，货轮能够安全进出该港口．请问当天什么时间段适合货轮进出此港口？
4. 如图，四边形ABCD中，已知AB∥CD，AB与CD之间的距离为4，AD＝5，CD＝3，∠ABC＝45°，点P，Q同时由A点出发，分别沿边AB，折线ADCB向终点B方向移动，在移动过程中始终保持PQ⊥AB，已知点P的移动速度为每秒1个单位长度，设点P的移动时间为x秒，△APQ的面积为y，则能反映y与x之间函数关系的图象是（ ）
5. 李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程s（千米）与行驶时间t（小时）的关系如图所示（中途休息、加油的时间不计．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升/千米，请根据图象解答下列问题：
（1）直接写出工厂离目的地的路程；
（2）求s关于t的函数表达式；
（3）当货车显示加油提醒后，问行驶时间t在怎样的范围内货车应进站加油？
6. 要修建一个圆形喷水池，在池中心竖直安装一根水管，水管的顶端安一个喷水头，记喷出的水与池中心的水平距离为x m，距地面的高度为y m．测量得到如下数值：
小腾根据学习函数的经验，发现y是x的函数，并对y随x的变化而变化的规律进行了探究．
下面是小腾的探究过程，请补充完整：
(1)在平面直角坐标系xOy中，描出表中各组数值所对应的点，并画出函数的图象；
(2)结合函数图象，出水口距地面的高度为_______m，水达到最高点时与池中心的水平距离约为_______m（结果保留小数点后两位）；
(3)为了使水柱落地点与池中心的距离不超过3.2m，如果只调整水管的高度，其他条件不变，结合函数图象，估计出水口至少需要_______（填“升高”或“降低”）_______m（结果保留小数点后两位）．
7. 小明近期计划阅读一本总页数不低于300页的名著，他制定的阅读计划如下：
若小明按照计划从星期开始连续阅读，10天后剩下的页数为，则与的图象可能为（ ）
8. 如图，有一个球形容器，小海在往容器里注水的过程中发现，水面的高度h、水面的面积S及注水量V是三个变量．下列有四种说法：①S是V的函数；②V是S的函数；③h是S的函数；④S是h的函数．其中所有正确结论的序号是（ ）
9. 如图1，在边长为4的等边中，点在边上，设的长度为自变量，以下哪个量作为因变量，使得，符合如图2所示的函数关系（ ）
10. 某公园内人工喷泉有一个竖直的喷水枪，喷出的水流路径可以看作是抛物线的一部分．记喷出的水流距喷水枪的水平距离为，距地面的竖直高度为，获得数据如下：
小景根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小景的探究过程，请补充完整：
(1)在平面直角坐标系中，描出以表中各对对应值为坐标的点，并画出该函数的图象；
(2)水流的最高点距喷水枪的水平距离为________m；
(3)结合函数图象，解决问题：公园准备在距喷水枪水平距离为处加装一个石柱，使该喷水枪喷出的水流刚好落在石柱顶端，则石柱的高度约为_____m．
11. 某公园有一个小型喷泉，水柱从垂直于地面的喷水枪喷出，水柱落于地面的路径形状可以看作是抛物线的一部分．记喷出的水柱距喷水枪的水平距离为（单x位：m），距地面的垂直高度为y（单位：m），现测得x与y的几组对应数据如下：
请根据测得的数据，解决以下问题：
(1)在平面直角坐标系中，描出以表中各组对应数据为坐标的点，并画出该函数的图象；
(2)结合表中所给数据或所画图象，得出水柱最高点距离地面的垂直高度为 m；
(3)求所画图象对应的二次函数表达式；
(4)公园准备在水柱下方的地面上竖直安装一根高的石柱，使该喷水枪喷出的水柱恰好经过石柱顶端，则石柱距喷水枪的水平距离为 m．（注：不考虑石柱粗细等其他因素）
12. 下面的四个选项中都有两个变量，其中变量y与变量x之间的函数关系可以用如图所示的图像表示的是（ ）
13. 已知y是x的函数，下表是x与y的几组对应值：
对于y与x的函数关系有以下4个描述①可能是正比例函数关系；②可能是一次函数关系；③可能是反比例函数关系；④可能是二次函数关系．所有正确的描述是（ ）
14. 在平面直角坐标系中，矩形，，，，点在边上，．点在边上运动，连接，点A关于直线的对称点为．若，，下列图像能大致反映与的函数关系的是（ ）．

15. 对于函数，小明探究了它的图像及部分性质．下面是他的探究过程，请补充完整：
(1)自变量x的取值范围是______；
(2)令b分别取0，1和，所得三个函数中的自变量与其对应的函数值如下表，则表中m的值是______，n的值是______；
(3)根据表中数据，补全函数，，的图像：
(4)结合函数，，的图像，写出函数的一条性质：______；
(5)点和点都在函数的图像上，当时，若总有，结合函数图像，直接写出和的大小关系．
16. 由于惯性的作用，行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”．某公司设计了一款新型汽车，现在对它的刹车性能（车速不超过150 km/h）进行测试，测得数据如下表：
(1)以车速v为横坐标，刹车距离s为纵坐标，在坐标系中描出表中各组数值所对应的点，并用平滑曲线连接这些点；
(2)由图表中的信息可知：
①该型汽车车速越大，刹车距离越 （填“大”或“小”）；
②若该型汽车某次测试的刹车距离为40 m，估计该车的速度约为 km/h；
(3)若该路段实际行车的最高限速为120 km/h，要求该型汽车的安全车距要大于最高限速时刹车距离的3倍，则安全车距应超过 m．
17. 函数的图象如图所示，在下列结论中：①该函数自变量的取值范围是；② 该函数有最小值；③方程有三个根；④如果和是该函数图象上的两个点，当时一定有．所有正确结论的序号是______．

18. 小朋在学习过程中遇到一个函数．
下面是小朋对其探究的过程，请补充完整：
(1)观察这个函数的解析式可知，x的取值范围是全体实数，并且y有______值（填“最大”或“最小”），这个值是______；
(2)进一步研究，当时，y与x的几组对应值如下表：
结合上表，画出当时，函数的图像；
(3)结合（1）（2）的分析，解决问题：
若关于x的方程有一个实数根为2，则该方程其它的实数根约为______（结果保留小数点后一位）．
19. 水龙头关闭不严会造成滴水．下表记录了30min内7个时间点的漏水量，其中t表示时间，y表示漏水量．
解决下列问题：
(1)在平面直角坐标系中，描出上表中以各对对应值为坐标的点，根据描出的点连线；
(2)结合表中数据写出滴水量y关于时间t的函数解析式______（不要求写自变量的取值范围）；
(3)在这种漏水状态下，若不及时关闭水龙头，估算一天的漏水量约为______mL．
20. 小明与小亮两人约定周六去博物馆参观学习．两人同时出发，小明乘车从甲地途径乙地到博物馆，小亮骑自行车从乙地到博物馆．已知甲地、乙地和博物馆在一条直线上，右图是两人分别与乙地的距离S（单位：km）与时间t（单位：min）的函数图像，在小明到达博物馆前，当两人相距1km时，t的值是______．
21. 数学活动课上，老师提出一个探究问题：
制作一个体积为，底面为正方形的长方体包装盒，当底面边长为多少时，需要的材料最省（底面边长不超过3dm，且不考虑接缝）．
某小组经讨论得出：材料最省，就是尽可能使得长方体的表面积最小．
下面是他们的探究过程，请补充完整：
(1)设长方体包装盒的底面边长为，表面积为．
可以用含的代数式表示长方体的高为．
根据长方体的表面积公式：长方体表面积．
得到与的关系式：___________________（）；
(2)列出与的几组对应值：
（说明：表格中相关数值精确到十分位）
表中_____________．
(3)在下面的平面直角坐标系中，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象：
(4)结合画出的函数图象，解决问题：
长方体包装盒的底面边长约为_________dm时，需要的材料最省；当长方体包装盒表面积为时，底面边长约为____________dm．
22. 如图所示是我国现存最完整的古代计时工具——元代铜壶滴漏，该滴漏从上至下通过多级滴漏，使得上层“壶”中的水可以匀速滴入最下层的圆柱形“壶”中，“壶”中漂浮的带有刻度的木箭随水面匀速缓缓上移，对准标尺就可以读出时辰，如果用表示时间，用表示木箭上升的高度，那么下列图象能表示与的函数关系的是（ ）
23. 已知A，B两地相距．甲、乙两辆货车分别从A，B两地同时出发，匀速相向而行．图1表示甲、乙两辆货车距A地的距离s（单位：）与行驶时间t（单位：）的数量关系；图2表示甲、乙两辆货车间的距离d（单位：）与行驶时间t（单位：）的数量关系．

根据以上信息得到以下四个推断：
①甲货车从A地到B地耗时6小时，即；
②出发后小时甲、乙两辆货车相遇，即；
③乙货车的速度是；
④点P的坐标是．
所有正确推断的序号是______．
24. 已知甲、乙两地相距，小徐和小马两人沿同一条公路从甲地到乙地，小徐骑自行车到达．小马骑摩托车比小徐晩出发，骑行时追上小徐，停留后继续以原速骑行．在整个行程中，两人与甲地的距离与小徐骑行时间的对应关系分别如图中线段和折线段所示，与的交点为．

(1)线段所对应的函数表达式为 ，相应自变量的取值范围是 ，线段所对应的函数表达式为 ，相应自变量的取值范围是 ；
(2)小马在段的速度为 ， ；
(3)求小马第二次追上小徐时与乙地的距离．
25. 电动汽车的续航里程也可以称作续航能力，是指电动汽车的动力蓄电池在充满电的状态下可连续行驶的总里程，它是电动汽车重要的经济性指标.高速路况状态下，电动车的续航里程除了会受到环境温度的影响，还和汽车的行驶速度有关.某科研团队为了分析续航里程与速度的关系，进行了如下的探究：
下面是他们的探究过程，请补充完整：
(1)他们调取了某款电动汽车在某个特定温度下的续航里程与速度的有关数据：
则设______为，______为，是的函数；
(2)建立平面直角坐标系，在给出的格点图中描出表中各对对应值为坐标的点，画出该函数的图象；
(3)结合画出的函数图象，下列说法正确的有______：
①随的增大面减小；
②当汽车的速度在60千米/小时左右时，汽车的续航里程度大；
③实验表明，汽车的速度过快或过慢时，汽车的续航里程都会变小．
(4)若想要该车辆的续航里程保持在500千米以上，该车的车速大约控制在______至______千米/小时范围内．
26. 在平面直角坐标系中，对于任意一点，规定：；比如．当时，所有满足该条件的点P组成的图形为（ ）
27. 某蔬菜批发基地为指导2023年的番茄销售，对历年的市场行情和供求情况进行了调查统计，得到番茄的售价x(单位：元/千克)与相应需求量(单位：吨)以及供给量(单位：吨)的几组数据：
(1)根据表中数据，供给量与售价x之间满足 函数关系(填“一次”、“二次”或“反比例”)，它的函数表达式为 ；需求量与售价x之间近似满足函数关系，它的函数表达式为 ．
(2)在同一平面直角坐标系中，画出(1)中所确定的函数的图象；
(3)结合函数图象，解决问题：为使番茄的供需平衡(即供给量与需求量相等)，售价应定为 元/千克．
28. 食用果蔬前，适当浸泡可降低农药的残留．某小组针对同种果蔬研究了不同浸泡方式对某种农药去除率的影响．
方式一：采用清水浸泡．
记浸泡时间为t分钟，农药的去除率为，部分实验数据记录如下：
方式二：采用不同浓度的食用碱溶液浸泡相同时间．
记食用碱溶液的浓度为，农药的去除率为，部分实验数据记录如下：
结合实验数据和结果，解决下列问题：
(1)通过分析以上实验数据，发现可以用函数刻画方式一中农药的去除率与浸泡时间t（分）之间的关系，方式二中农药的去除率与食用碱溶液的浓度之间的关系，请分别在下面的平面直角坐标系中画出这两个函数的图象；
(2)利用方式一的函数关系可以推断，降低该种农药残留的最佳浸泡时间约为______分钟；
(3)利用方式一和方式二的函数关系可以推断，用食用碱溶液浸泡含该种农药的这种果蔬时，要想不低于清水浸泡的最大去除率，食用碱溶液的浓度中，x的取值范围可以是_____．
29. A，B，C三种上宽带网方式的月收费金额yA（元），yB（元），yC（元）与月上网时间x（小时）的对应关系如图所示．以下有四个推断：
①月上网时间不足35小时，选择方式A最省钱；
②月上网时间超过55小时且不足80小时，选择方式C最省钱；
③对于上网方式B，若月上网时间在60小时以内，则月收费金额为60元；
④对于上网方式A，若月上网时间超出25小时，则超出的时间每分钟收费0.05元．
所有合理推断的序号是（ ）
30. 某公司安排A，B两个车间生产同一款产品，每天这两个车间都是每小时生产件该产品，且生产前没有产品积压，生产一段时间后再安排产品装箱，当天全部产品装箱完毕结束生产．设每天的产品生产时间为x（单位：小时），生产过程中未装箱产品数量为y（单位：件）．
(1)某天A车间生产过程中，未装箱产品数量y与产品生产时间x的关系如图所示．

结合图像：
①当时，写出y关于x的函数表达式；
②开始安排产品装箱时，未装箱产品数量为_____________件；
③当天全部产品装箱完毕时，产品生产时间为_____________小时．
(2)同一天B车间生产过程中，开始安排产品装箱后，未装箱产品数量y与产品生产时间x近似满足函数关系．记这一天A车间开始安排产品装箱时，产品生产时间为，B车间开始安排产品装箱时，产品生产时间为，则_________（填“＞”，“＝”或“＜”）．A．①②
B．①③
C．②③
D．①②③
11.0
9.0
9.0
7.0
5.5
4.5
3.5
3.0
3.0
2.0
1.0
0.8
1.0
1.3
1.9
2.6
3.2
4.3
4.0
5.0
7.1
11.5
11.8
10.0
10.3
8.9
8.1
7.7
7.8
7.0
8.0
9.1
12.5
C
0.990
0.989
0.990
0.990
0.990
0.990
0.990
0.988
0.990
0.990
0.990
x（h）
…
11
12
13
14
15
16
17
18
…
y（）
…
189
137
103
80
101
133
202
260
…
A．
B．
C．
D．
x/m
0
0.5
1
1.5
2
2.5
3
3.37
y/m
2.44
3.15
3.49
3.45
3.04
2.25
1.09
0
星期
一
二
三
四
五
六
日
页数
15
20
15
10
20
40
30
A．
B．
C．
D．
A．①③
B．①④
C．②③
D．②④
A．的面积
B．的周长
C．的面积
D．的周长
0.0
1.0
2.0
3.0
4.5
1.6
3.7
4.4
3.7
0.0
水平距离x/m
0
1
2
3
4
5
6
…
垂直高度y/m
0.7
1.6
2.3
2.8
3.1
3.2
3.1
…
A．圆的面积y与它的半径x；
B．正方形的周长y与它的边长x；
C．用长度一定的铁丝围成一个矩形，矩形的面积y与一边长x；
D．小明从家骑车去学校，路程一定时，匀速骑行中所用时间y与平均速度x；
x
…
3
6
…
y
…
2
1
…
A．①②
B．②③
C．③④
D．①④
A．
B．
C．
D．
…
0
1
2
3
…
…
3
2
1
0
1
2
3
…
…
4
2
1
2
3
4
…
…
1
0
0
1
…
车速v（km/h）
0
30
60
90
120
150
刹车距离s（m）
0
7.8
19.2
34.2
52.8
75
x
0
1
2
3
4
…
y
0
2
1
0
2
…
时间t/min
0
5
10
15
20
25
30
漏水量y/mL
0
15
30
45
60
75
90
…
0.5
1.0
1.5
2.0
2.5
3.0
…
80.5
42.0
31.2
28.5
31.3
A．
B．
C．
D．
速度（千米/小时）
10
20
30
40
60
80
100
120
140
160
续航里程（千米）
100
340
460
530
580
560
500
430
380
310
A．
B．
C．
D．
售价x/元/千克
…
2
3
4
5
6
…
需求量/吨
…
9.5
8.875
8
6.875
5.5
…
供给量/吨
…
1
2
3
4
5
…
t（分）
5
8
10
12
15
20
30
50
57
52
37
33
2
5
7
10
12
15
43
52
57
76
57
25
A．①②
B．①③
C．①③④
D．②③④