

2024北京中考名校密题:数学最后冲刺30题-观察猜想与证明
展开1. 现有颗外观和大小都完全相同的小球,已知颗球的质量相等,另外一颗球的质量略大一些.小颖想用一架托盘天平称出这颗质量较大的球.她思考后发现最少称次就一定能找出这颗球,则的值等于______.
2. 某娱乐设施每次能够容纳4人一组进场游玩,甲、乙、丙、丁排队等候,甲前面有若干人,乙排在甲后面,中间隔着2人,丙排在乙后面,中间隔着1人,丁排在丙后面,中间隔着1人,丁后面也有若干人.下列说法:①如果甲和乙同一组,那么丙和丁也同一组;②如果甲和乙不同一组,那么丙和丁也不同一组;③如果丙和丁同一组,那么甲和乙也同一组;④如果丙和丁不同一组,那么甲和乙也不同一组.正确的个数为( )
3. 直角坐标系,通常称为笛卡尔直角坐标系,它是以法国哲学家、数学家笛卡尔的名字命名的.笛卡尔于1637年发明了坐标系,导入运动着的点的坐标概念.他使用代数的方法研究几何,创立了解析几何学,被认为是解析几何之父.这种用代数的方法解决几何问题的研究方法体现的数学思想是( )
4. 问题:我们知道平面内两条直线的位置关系有两种:相交、平行,那在同一平面内多条直线的位置关系又如何?现准备研究在同一平面内,有且仅有两条直线平行的条直线产生的交点个数情况.(是不小于3的正整数)
(1)【初探】当时,交点个数有________个;当时,交点个数有________个;
(2)【再探】当时,交点个数最多有________个;
(3)【归纳】请你求出在同一平面内,有且仅有两条直线平行的条直线最多能产生多少个交点;
(4)【运用】在同一平面内,有且仅有两条直线平行的12条直线最多能产生多少个交点,此时,图中共有多少对对顶角?
5. 六名运动员比赛中国象棋每两人赛一局第一天与各赛了局与各赛了局赛了局而且和和之间都还没赛过那么已赛了多少局( )
6. 实践与探究题
问题:直角三角形除了三边之间、两个锐角之间有特殊的关系外,斜边上的中线有什么性质呢?
丽丽同学利用直角三角形纸片进行了如下的折叠实验:
(1)观察发现
① 观察丽丽同学的折叠实验,你发现线段CD与AB之间有何数量关系?在图(1)所示的Rt△ ABC中,∠C=90°,CD是斜边AB上中线.请根据图(1)证明你的猜想.
② 根据上面的探究,总结直角三角形斜边上的中线性质.
(2)拓展应用:如图(2),CD是Rt△ ABC的斜边AB上的高,若CD=5,则Rt△ ABC面积的最小值等于______.
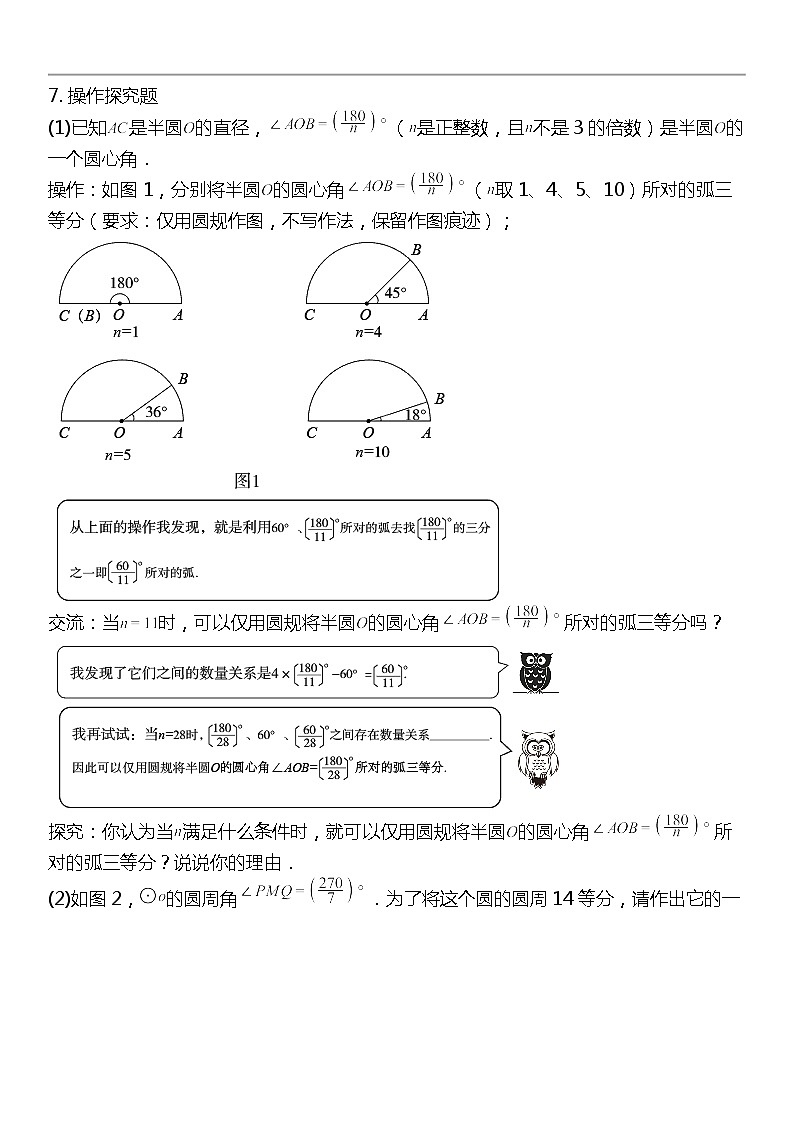
7. 操作探究题
(1)已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.
操作:如图1,分别将半圆的圆心角(取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);
交流:当时,可以仅用圆规将半圆的圆心角所对的弧三等分吗?
探究:你认为当满足什么条件时,就可以仅用圆规将半圆的圆心角所对的弧三等分?说说你的理由.
(2)如图2,的圆周角.为了将这个圆的圆周14等分,请作出它的一条14等分弧(要求:仅用圆规作图,不写作法,保留作图痕迹).
8. 如图,在△ABC中,∠C=90°,BC=1,AC=2,、、…都是正方形,且、、…在AC边上,、、…在AB边上.则线段的长用含n的代数式表示为______________.(n为正整数)
9. 若不等式(组)只有个正整数解(为自然数),则称这个不等式(组)为阶不等式(组).
我们规定:当时,这个不等式(组)为0阶不等式(组).
例如:不等式只有4个正整数解,因此称其为4阶不等式.
不等式组只有3个正整数解,因此称其为3阶不等式组.
请根据定义完成下列问题:
(1)是 阶不等式;是 阶不等式组;
(2)若关于的不等式组 是4阶不等式组,求的取值范围;
(3)关于的不等式组 的正整数解有,,,,…,其中….如果 是阶不等式组,且关于的方程的解是 的正整数解,直接写出的值以及的取值范围.
10. 在数学探究课上,小明在探究圆周角和圆心角之间的数量关系时,按照圆周角与圆心的不同位置关系作出了如下图所示三个图进行探究小明的上述探究.过程体现的数学思想是( )
11. 电脑系统中有个“扫雷”游戏,游戏规定:一个方块里最多有一个地雷,方块上面如果标有数字,则是表示此数字周围的方块中地雷的个数. 如图1中的“3”就是表示它周围的八个方块中有且只有3个有地雷.如图2,这是小明玩游戏的局部,图中有4个方块已确定是地雷(标旗子处),其它区域表示还未掀开,问在标有“A”~“G”的七个方块中,能确定一定是地雷的有________(填方块上的字母).
12. 数学课上,老师给同学们布置了一个探究任务:
请你观察各组数据的特征,算一算,结合三组数据的变化规律,提出一个合理的猜想:________
13. 公园计划砌一个形状如图1的水池(图中长度单位:m),后有人建议改为如图2的形状,且外圆直径不变.
(1)请你计算两种方案中的圆形水池的周长,确定哪一种方案砌的圆形水池的周边需要的材料多.
(2)如图3,如果将图2中的小圆半径改为r1,r2,r3,且r1+r2+r3=r,其他条件不变,猜想(1)中的结论是否改变,并说明理由.
(3)如图4,若将图3中三个小圆改为n个小圆,小圆半径分别为r1,r2,…,rn,且r1+r2+…+rn=r,直接写出图4中所有圆的周长总和.
(4)元宝是中国古代的货币,在今天也有着富贵吉祥的寓意,王师傅准备建设一个形如元宝的花坛,如图5,花坛是由4个半圆所围成,最大半圆的半径为2.1米,直接写出花坛周边需要的材料总长(结果保留π).
14. 给定二元数对(p,q),其中或1,或1.三种转换器A,B,C对(p,q)的转换规则如下:
(1)在图1所示的“A—B—C”组合转换器中,若输入,则输出结果为________;
(2)在图2所示的“①—C—②”组合转换器中,若当输入和时,输出结果均为0,则该组合转换器为“____—C—____”(写出一种组合即可).
15. 在中国古代诗词中,有很多诗句体现了数学的某些意境,如“明月松间照,清泉石上流”体现了对称的意境;“孤帆远影碧空尽,唯见长江天际流”体现了极限(或无限)的意境,请你再举出一例并说明其蕴涵的数学意义:__.
16. 八(1)班有39位同学,他们每人将自己的学号作为n的取值()代入式子,结果发现式子的值都是质数,于是他们猜想:“对于所有的自然数,式子的值都是质数.”你认为这个猜想正确吗?验证一下的情形.
17. (1)图中三条线段a,b,c,哪一条和线段d在同一条直线上?请你先观察,再用直尺验证一下.
(2)图中两条线段a与b的长度相等吗?
18. 数学课外活动小组的同学在学习了完全平方公式之后,针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究,请阅读以下探究过程并解决问题.
猜想发现:由;;;;;
猜想:如果,,那么存在(当且仅当时等号成立).
猜想证明:∵
∴①当且仅当,即时,,∴;
②当,即时,,∴.
综合上述可得:若,,则成立(当且仅当时等号成立).
猜想运用:(1)对于函数,当取何值时,函数的值最小?最小值是多少?
变式探究:(2)对于函数,当取何值时,函数的值最小?最小值是多少?
拓展应用:(3)疫情期间、为了解决疑似人员的临隔离问题.高速公路榆测站入口处,检测人员利用检测站的一面墙(墙的长度不限),用63米长的钢丝网围成了9间相同的长方形隔离房,如图.设每间离房的面积为(米2).问:每间隔离房的长、宽各为多少时,可使每间隔离房的面积最大?最大面积是多少?
19. 一般地,如果(n为正整数,且),那么x叫做a的n次方根,下列结论中正确的是( )
20. 定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,是的外角.
求证:.
下列说法正确的是( )
21. 下表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过,因而人们把这个表叫做杨辉三角,请你根据杨辉三角的规律补全下表第四行空缺的数字是______.
22. 材料一:北师大版数学教材九年级上册第四章,对“黄金分割比”的定义如下:
“如图 ,点C把线段AB分成两条线段AC和BC,如果=,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,=叫做黄金比.”根据定义不难发现,在线段AB另有一点D把线段AB分成两条线段AD和BD,满足=,所以点D也是线段AB的黄金分割点.
材料二:对于实数:a1<a2<a3<a4,如果满足(a3﹣a1)2=(a4﹣a3)(a4﹣a1),(a4﹣a2)2=(a2﹣a1)(a4﹣a1)则称a3为a1,a4的黄金数,a2为a1,a4的白银数.
请根据以上材料,回答下列问题
(1)如图 ,若AB=4,点C和点D是线段AB的黄金分割点,则AC= ,CD= .
(2)实数0<a<b<1,且b为0,1的黄金数,a为0,1的白银数,求b﹣a的值.
(3)实数k<n<m<t,t=2|k|,m,n分别为k,t的黄金数和白银数,求的值.
23. 已知,在计算:的过程中,如果存在正整数,使得各个数位均不产生进位,那么称这样的正整数为“本位数”.例如:2和30都是“本位数”,因为没有进位,没有进位;15和91都不是“本位数”,因为,个位产生进位,,十位产生进位.则根据上面给出的材料:
(1)下列数中,如果是“本位数”请在后面的括号内打“√”,如果不是“本位数”请在后面的括号内画“×”.
106( );111( );400( );2015( ).
(2)在所有的四位数中,最大的“本位数”是 ,最小的“本位数”是 .
(3)在所有三位数中,“本位数”一共有多少个?
打印为PDFA.1
B.2
C.3
D.4
A.类比思想
B.分类讨论思想
C.数形结合思想
D.公理化思想
A.1
B.2
C.3
D.4
A.公理化思想
B.分类讨论思想
C.转化思想
D.建模思想
第一组数据
;
;
;
;
;
第二组数据
;
;
;
;
;
第三组数据
;
;
;
;
.
A.16的4次方根是2
B.32的5次方根是
C.当n为奇数时,2的n次方根随n的增大而减小
D.当n为奇数时,2的n次方根随n的增大而增大
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
2024北京中考名校密题:数学最后冲刺30题-数与式-实数: 这是一份2024北京中考名校密题:数学最后冲刺30题-数与式-实数,共13页。试卷主要包含了001),即_____., 经研究发现等内容,欢迎下载使用。
2024北京中考名校密题:数学最后冲刺30题-数与式-因式分解: 这是一份2024北京中考名校密题:数学最后冲刺30题-数与式-因式分解,共5页。试卷主要包含了 阅读下面材料, 阅读, 分解因式, 阅读材料并回答问题, 阅读下列材料, 阅读材料等内容,欢迎下载使用。
2024北京中考名校密题:数学最后冲刺30题-数与式-分式: 这是一份2024北京中考名校密题:数学最后冲刺30题-数与式-分式,共11页。试卷主要包含了 阅读理解, 通分等内容,欢迎下载使用。












